Глава 5 Реализация симплекс-метода на компьютере

Распечатайте себе лекции

Пример 4.1. Фирма выпускает три вида кожаных изделий A, B и C. На изготовление единицы продукции A затрачивается 0,2 ч работы дубильного участка, 0,6 ч раскройного участка, 0 ч завершающего участка. На изготовление единицы продукции B – 0,3; 0,5 и 0 ч; на изготовление единицы продукции C – 0,4; 0,4 и 0,8 соответственно. Прибыль от единицы продукции вида A составляет 6 ден.ед., вида B – 7 ден.ед., вида C – 10 ден.ед. В течение месяца рабочее время каждого участка ограничено следующим образом:

Дубильного участка – 320 ч; Раскройного участка – 400 ч; Завершающего участка – 160 ч.

Необходимо: 1) записать данные задачи в таблицу; 2) составить экономическую модель; 3) найти план выпуска продукции, чтобы прибыль была максимальной.

1) Таблица.

Ресурсы ( ч )	А	В	С	Ограничения на ресурсы ( ч )
Дубильный участок	0,2	0,3	0,4
Раскройный участок	0,5	0,5	0,4
Завершающий участок			0,8
Прибыль (ден.ед.)

2) Экономическая модель.

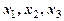– количество рабочего времени на изготовление продукции A, B и C соответственно.

Прямая задача линейного программирования	Двойственная задача

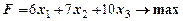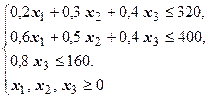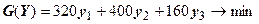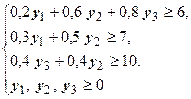3) Решение задачи на компьютере.

1. Создадим форму для ввода условий задачи. <= знак 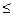, >= знак .

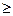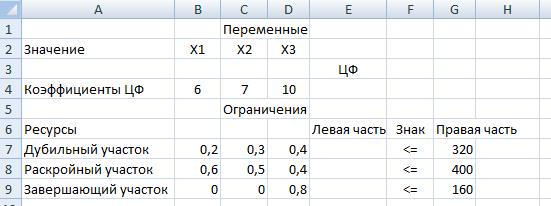
2. Оптимальные значения вектора 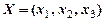будут в ячейках B3:D3, оптимальное значение целевой функции – в ячейке E4.

3. Введём зависимость для целевой функции:

· курсор в ячейку E4, курсор на кнопку «Мастер функций»

· на экране появляется диалоговое окно Мастер функций шаг 1 из 2

· курсор в окно Категория на Математические

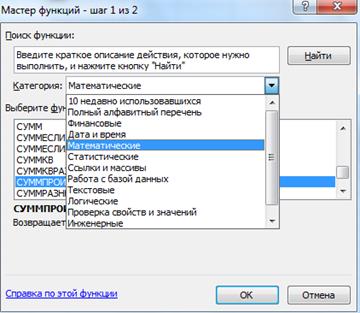
· курсор в окноВыберите функцию на СУММПРОИЗВ

· курсор на ОК

· на экране появится окно СУММПРОИЗВ

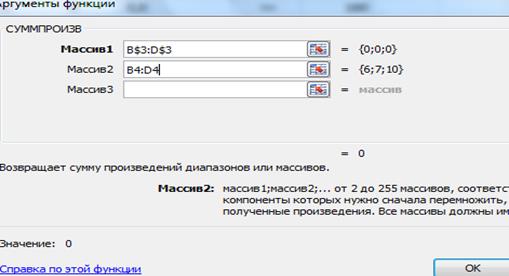
· в строку Массив 1 ввести B$3:D$3

· в строку Массив 2 ввести B4:D4

· ОК. В ячейке Е4 появится 0

4. Введём зависимости для ограничений:

· Курсор в ячейку Е4. Копировать. Вставить в ячейки Е7, Е8 и Е9

5. Данные\Поиск решения\

· Появится окно Поиск решения

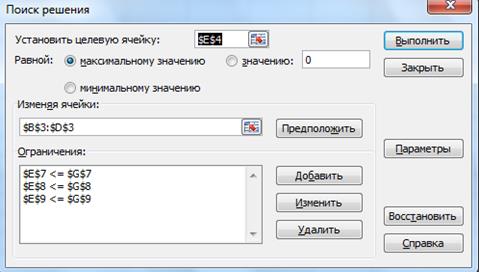
· В строке Установить целевую функцию ввести $E$4. Отметить Максимальному значению

· Курсор в строку Изменяя ячейки.Введём адрес переменных B$3:D$3

6. Введём ограничения:

· Указатель мышки на кнопку Добавить. Появится окно Добавление ограничений

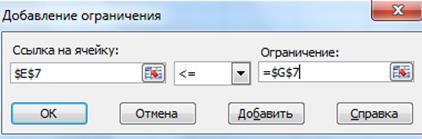
· Введём ограничения. ОК

7. Введём параметры для решения ЗЛП

· В окне Поиск решения указатель мыши на кнопку Параметры. Появится окно Параметры поиска решения

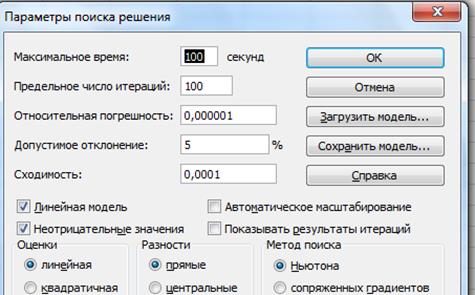
· Установим Линейная модель (будет симплекс-метод) и Неотрицательные значения, оценки линейные, разности прямые, метод поиска Ньютона

· ОК.В окне Поиск решения нажать кнопку Выполнить

· Появится окно Результаты поиска решения

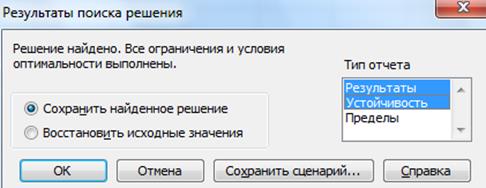
· Указать тип отчёта: нажать Результаты,Устойчивость

· ОК. Появится таблица с заполненными ячейками B3:D3, Е7:Е9 и максимальным значением целевой функции в ячейке Е4

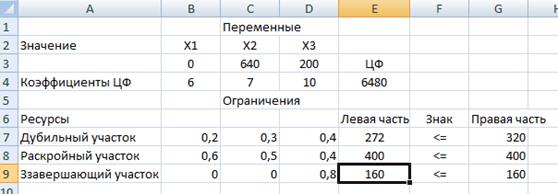
Рисунок 5.1

· Появятся 2 новых листа: Отчёт по результатам 1, Отчёт по устойчивости 1

Microsoft Excel 12.0 Отчет по результатам
Рабочий лист: [Симплекс.xlsx]Лист1
Отчет создан: 07.01.2011 19:43:15
Целевая ячейка (Максимум)
Ячейка	Имя	Исходное значение	Результат
$E$4	Коэффициенты ЦФ ЦФ
Изменяемые ячейки
Ячейка	Имя	Исходное значение	Результат
$B$3	X1
$C$3	X2
$D$3	X3
Ограничения
Ячейка	Имя	Значение	Формула	Статус	Разница
$E$7	Дубильный участок Левая часть		$E$7<=$G$7	не связан.
$E$8	Раскройный участок Левая часть		$E$8<=$G$8	связанное
$E$9	Завершающий участок Левая часть		$E$9<=$G$9	связанное

В отчёте по результатам та же информация, что и на рисунке 5.1.

Рассмотрим более подробно отчёт по устойчивости.

Microsoft Excel 12.0 Отчет по устойчивости
Рабочий лист: [Симплекс.xlsx]Лист1
Отчет создан: 07.01.2011 19:43:15
Изменяемые ячейки
		Результ.	Нормир.	Целевой	Допустимое	Допустимое
Ячейка	Имя	значение	стоимость	Коэффициент	Увеличение	Уменьшение
$B$3	X1		-2,4		2,4	1E+30
$C$3	X2				5,5
$D$3	X3				1E+30	4,4

Трактовка значений таблицы. Если будем менять только один коэффициент целевой функции 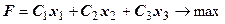, то оптимальное решение прямой ЗЛП не изменится.

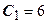. Допустимое увеличение 2,4. Допустимое уменьшение 1E+30, т.е. любое.

Тогда 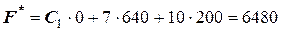. Х1=0, поэтому изменение коэффициента С1 не меняет оптимальное значение целевой функции.

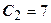. Допустимое увеличение 5,5. Допустимое уменьшение 2.

Увеличение ,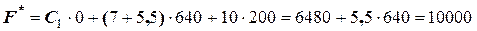

Уменьшение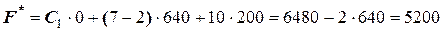

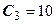. Допустимое увеличение любое. Допустимое уменьшение 4,4.

Ограничения
		Результ.	Теневая	Ограничение	Допустимое	Допустимое
Ячейка	Имя	значение	Цена	Правая часть	Увеличение	Уменьшение
$E$7	Дубильный участок Левая часть				1E+30
$E$8	Раскройный участок Левая часть
$E$9	Завершающий участок Левая часть		5,5

Трактовка значений таблицы.

1) Теневая цена раскройного участка самая высокая, поэтому это самый дефицитный ресурс. Теневая цена дубильного участка равна 0. Ресурс не используется полностью, он не является дефицитным.

2) Если будем менять только один коэффициент целевой функции 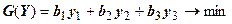, то оптимальное значение двойственной задачи не изменится.

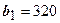. Допустимое увеличение любое, т.к. ресурс не является дефицитным. Допустимое уменьшение 48.

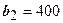. Допустимое увеличение 80. Допустимое уменьшение 320.

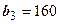. Допустимое увеличение 240. Допустимое уменьшение 160.