Построение линейной регрессионной модели на основе ПФЭ.

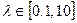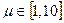Область возможного изменения факторов объекта исследования представляется соответственно и ед.вр.^-1. В качестве центра плана эксперимента выберем точку М⁰ в факторном пространстве с координатами λ=5ед.вр.^-1, μ=6ед.вр.^-1, интервалы варьирования факторов соответственно равны λ=1,4 ед.вр.^-1, μ=1,5ед.вр.^-1

Для стандартизации масштабов факторов вычислим значения нижнего и верхнего уровня согласно выражению (2.2) в [5] и сведем результаты в таблицу 1.

Условия проведения ПФЭ в точке М⁰

Таблица 1.

Характеристика плана	Стандартный масштаб xi	Натуральный масштаб
x1= λ, ед.вр.-1	x2= μ, ед.вр.-1
Нулевой уровень
Верхний уровень	+1	6,4	7,5
Нижний уровень	-1	3,6	4,5

Составим матрицу эксперимента с учетом рандомизации опытов. В таблице 2 представлены результаты параллельных опытов и вычислены среднее значение отклика и дисперсия для каждой точки факторного пространства соответственно соотношениям (2.3) и (2.4) в [5].

Результаты эксперимента.

Таблица 2.

№	x0	x1	x2	y1	y2	y3	y4	y5	ycp	s2yi
		-1	-1	209,79	186,17	188,54	188,05	194,36	193,38	93,56
			-1	120,78	119,29	123,12	124,35	124,29	122,37	5,04
		-1		100,21	123,07	121,39	118,99	116,45	116,02	84,39
				31,58	27,29	22,37	34,64	33,90	29,96	26,17

Проведем анализ воспроизводимости опыта на основе критерия Кохрена в соответствии с (2.5) в [5]: G_расч=0,447, табличное значение критерия определяем при уровне значимости α=0,05 и степенях свободы γ₁=m-1=4, γ₂=N=4, получаем G_табл(α;γ₁;γ₂)=0,639. Так как G_расч< G_табл, опыт является воспроизводимым, и его результаты можно использовать для оценки коэффициентов регрессионного уравнения.

В соответствии с расчетным соотношением (2.6) в [5] можно определить коэффициенты регрессионной модели. Для анализа значимости коэффициентов необходимо вычислить погрешности определения коэффициентов модели и расчетное значение t – критерия Стьюдента на основании соотношений (2.7)-(2.9) в [5]. Результаты расчетов приведены в таблице 3.

Результаты анализа значимости коэффициентов.

Таблица 3.

	b0	b1	b2
коэффициенты регрессионной модели	115,43	-39,27	-42,44
tрасч	71,390	24,287	26,248
вывод	зн	зн	зн

Для принятия решения о значимости коэффициентов уравнения регрессии расчетное значение критерия Стьюдента t_расч сравнивается с табличным значением. Табличное значений критерия Стьюдента t_табл выбирается при уровне значимости α=0,05 и степени свободы γ=N(m-1)=16, t_табл=2,12. Неравенство t_расч >t_табл выполняется для всех коэффициентов регрессионной модели, поэтому они все считаются значимыми и включаются в модель.

Проверка адекватности построенной модели выполняется в соответствии с критерием Фишера (2.11) в [5]. Согласно выражению (2.9) в [5] дисперсия воспроизводимости равна s²_воспр=52,29, остаточная дисперсия в соответствии с (2.10) в [5] составляет s²_ост= 56,63, Расчетное значение критерия Фишера (2.11) в [5] равно F_расч=1,09. Табличное значений критерия Фишера F_табл выбирается при уровне значимости α=0,05 и степенях свободы 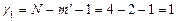и 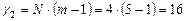, F_табл=4,49. Неравенство F_расч< F_табл выполняется, поэтому построенная регрессионная модель считается адекватной экспериментальным данным.

Перейдем от кодированных значений факторов к натуральному исчислению в соответствии с выражением (2.2) в [5] и условиями проведения эксперимента в таблице 1:

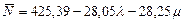. (3)

Таким образом, выражение (3) представляет характер изменения среднего числа обработанных заявок в вычислительной системе в течение времени T в области изменения параметров системы 3,6≤λ≤6,4 ед.вр.^-1, 4,5≤μ≤7,5 ед.вр.^-1.

Для определения направления возрастания функции отклика вычислим градиент:

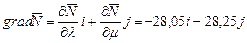. (4)

Выражение (4) определяет направление поиска оптимума функции отклика из текущего центра плана с координатами М⁰= (5,6).

На этом выполнение первого этапа задания на научно-исследовательскую практику (осенний семестр) завершается.