Вопрос № 10 Далее рассмотрим особенности представления в ЭВМ вещественных чисел.
Вещественные числа в памяти ЭВМ могут быть записаны в двух формах:
1. С фиксированной точкой.
2. С плавающей точкой.
В форме с фиксированной точкой все числа представляются в виде последовательности цифр с постоянным положением точки, отделяющей целую часть от дробной (практически во всех языках программирования для разделения целой и дробной части используется точка, а не запятая).
Пример 4. В случае десятичной системы счисления, пяти разрядов для представления целой части и восьми разрядов для представления дробной части, числа 632, 24.1254 и ‑0.0125012 будут иметь вид:
+00632.00000000 +00024.12540000 -00000.01250120
Данная форма представления вещественных чисел является наиболее простой, но имеет небольшой диапазон представления, т.к. зачастую приходится хранить большое количество незначащих нулей.
В форме с плавающей точкой каждое число представляется в виде двух групп чисел, называемых мантиссой и порядком. При этом мантисса – наибольшее вещественное число по абсолютной величине меньшее 1, а порядок – целое число. Таким образом, любое вещественное число может быть представлено в виде:
±M×10±R,
где M – мантисса числа ( 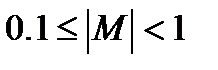 ),
),
R – порядок числа
Пример 5. В форме с плавающей точкой числа из предыдущего примера будут иметь вид:
+0.632×10+3 +0.241254×10+2 -0.125012×10-1
Далее рассмотрим особенности представления дробной части вещественного числа в двоичной системе счисления. Для перевода числа Q (|Q|<1), записанного в десятичной системе счисления, в двоичную систему счисления, можно использовать следующий алгоритм:
1. Число Q умножается на 2.
2. Целая часть полученного результата приписывается справа к двоичной записи числа.
3. Дробная часть результата, полученного в п. 1 принимается за число Q.
4. Осуществляется переход к п. 1.
Процесс продолжается вплоть до достижения заданной точности или до того момента, когда в п. 3 получится число 0.
Пример 6. Представить в двоичной системе счисления число 0.3125.
0.3125 x 2 = 0.625 ® 0
0.625 x 2 = 1.25 ® 1
0.25 x 2 = 0.5 ® 0
0.5 x 2 = 1.0 ® 1
0.0 {x 2 = 0}.
Таким образом, 0.3125(10) = 0.0101(2),
Пример 7. Представить в двоичной системе счисления число 0.428, если для записи дробной части этого числа выделен 1 байт.
1) 0.428 x 2 = 0.856 ® 0
2) 0.856 x 2 = 1.712 ® 1
3) 0.712 x 2 = 1.424 ® 1
4) 0.424 x 2 = 0.848 ® 0
5) 0.848 x 2 = 1.696 ® 1
6) 0.696 x 2 = 1.392 ® 1
7) 0.392 x 2 = 0.784 ® 0
8) 0.784 x 2 = 1.568 ® 1
… … … … …
0.428(10) » 0.01101101(2)
Очевидно, в общем случае для перевода вещественного числа (без знака) в 2 с/с необходимо перевести отдельно целую часть в 2 с/с (делением в столбик на 2), отдельно – дробную (по вышеописанному алгоритму), затем объединить (сложить) полученные результаты.
Пример 8.
9.3125(10) = 9(10) + 0.3125(10) = 1001(2) + 0.0101(2) = 1001.0101(2).
Приведенный пример показывает, что вещественные числа хранятся в памяти ПК, вообще говоря, приближенно. {Этот факт следует учитывать при написании программ. Например, если в память ПК занести число Q равное 0.428, а затем выполнить проверку условия «Q=0.428?», то, вполне вероятно, будет получен результат «не верно».}
Для перевода двоичного числа anan-1…a1a0 . a-1a-2…a1-sa-s в десятичную систему счисления используется формула
an×2n+an-1×2n-1+ …+a1×21+a0×20+ a-1×2-1+a-2×2-2+…+a1-s×21-s+a-s×2-s
Пример 9. Перевести в десятичную систему счисления двоичное число, полученное в примере 7.
0.01101101(2) = 0×20+0×2-1+1×2-2+1×2-3+0×2-4+1×2-5+1×2-6+0×2-7+1×2-8 = 0.42578125 (не равно 0.428!)
Вопрос № 11 Следует отметить, что запись чисел в двоичной системе счисления является довольно громоздкой. Поэтому при программировании вместо двоичной системы счисления часто используется шестнадцатеричная, в которой для отображения цифр больших 9 используются буквы A=10, B=11, C=12, D=13, E=14, F=15. Для перевода чисел из двоичной системы счисления в шестнадцатеричную каждой шестнадцатеричной цифре ставят в соответствие группу из четырех двоичных разрядов (табл. 1).
Таким образом, чтобы перевести двоичное число в шестнадцатеричное, необходимо разбить его на группы по 4 разряда, приписав в случае необходимости слева нули, после чего сопоставить полученным группам шестнадцатеричные цифры согласно табл.
Пример 10. Перевести в шестнадцатеричную систему счисления двоичное число 1010101101001010111010.
Разобьем данное число на группы по 4 разряда. Т.к. всего число содержит 22 разряда, то слева необходимо приписать два нуля: 0010 1010 1101 0010 1011 1010. Воспользовавшись табл. 1, получаем: 1010101101001010111010(2) = 2AD2BA(16)
Замечание. Чтобы отличать шестнадцатеричные числа от десятичных, в конце записи шестнадцатеричного числа указывается символ h (hexadecimal – шестнадцатеричный)
Пример 11. 2035h = 10000000110101(2) = 8245 (проверить самостоятельно).
Вопрос № 12
Представление текстовой информации
{Как и любая другая информация, символьные данные должны храниться в памяти ЭВМ в двоичном виде.} Для хранения символьных данных в памяти ЭВМ каждому символу ставится в соответствие некоторое неотрицательное число, называемое кодом символа, и это число записывается в память ЭВМ в двоичном виде. Соответствие между набором символов и числами называется кодировкой символов.
В ЭВМ, как правило, используются 8-разрядные коды символов. Это позволяет закодировать 256 различных символов, {чего вполне достаточно для представления многих символов, используемых на практике.} Поэтому для кода символа достаточно выделить в памяти один байт.
В ПК наряду с более современными (Windows-1251, KOI-8 и др.) используется система кодировки ASCII (American Standard Code for Information Interchange). Кодировка ASCII имеет основной стандарт и его расширение. Основной стандарт использует для кодирования символов коды 00h – 7Fh, расширение стандарта – коды 80h – FFh. Основной стандарт является международным и используется для кодирования управляющих символов, цифр и букв латинского алфавита. В расширении стандарта кодируются символы псевдографики и букв национального алфавита. Кодировка ASCII некоторых символов приведена в табл.
Пример 12. Название шведской музыкальной группы “ABBA” кодируется следующим образом:
а) в 2 с/с: 01000001010000100100001001000001;
б) в 16 с/с: 41424241.
Вопрос № 13
