Вычисление интегралов, решение уравнений и систем

Краткие теоретические сведения

В Scilab вычисление определенного интеграла методом трапеций реализовано функцией

Inttrap(x,y),

где x –вектор значений аргумента подынтегральной функции на отрезке интегрирования, y –вектор значений, полученных при вычислении подынтегральной функции для элементов вектора x.

Например, для вычисления 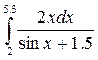нужно выполнить следующий набор команд:

Фрагмент программы x =2:0.01:5.3 y =2*x./(sin(x)+1.5) integral = inttrap(x,y)disp(integral)

Результат 30.436962

Для вычисления определенного интеграла с использованием алгоритма квадратурных формул предназначена функция

Integrate(fun, x, a, b, ,er1 ,er2),

где fun– подынтегральная функция в символьном виде, x – переменная интегрирования в символьном виде, a, b –пределы интегрирования, er1,er2 –абсолютная и относительная погрешности интегрирования (необязательные параметры).

Например, для вычисления 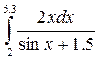нужно задать:

Фрагмент программы z=integrate('2*x./(sin(x)+1.5)', 'x', 2, 5.3)disp(z)

Результат 30.437056

Универсальная команда интегрирования:

[integral,err]=intg(a, b, name ,er1,er2),

где a, b –пределы интегрирования, name – имя подынтегральной функции (может быть задана с помощью внешней функции), er1,er2 –абсолютная и относительная погрешности интегрирования (необязательные параметры). Функция intgвозвращает значение интеграла (integral) и погрешность вычислений (err).

Внешнюю функцию можно задать командой

deff('переменная=имя функции(параметр)', 'символьное представление функции') Например, deff('y=F(x)', 'y=2*x./(sin(x)+1.5)').или

function переменная = имя функции(параметр-аргумент функции)

операторы, вычисляющие значение функции

endfunctionНапример, function y=f(t) y=t^2/sqrt(3+sin(t)) endfunctionилиfunction y=f(t),y=t^2/sqrt(3+sin(t)),endfunction

Ниже приводится пример вычисления интеграла .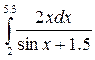

Фрагмент программы function y=f(x) y=2*x./(sin(x)+1.5)endfunctionz=intg(2,5.3,f), disp(z)

Результат   30.437056

Для решения нелинейных уравнений в Scilab используется функция

Fsolve(x0,f) ,

где x0 –начальное приближение корня, f– функция, описывающая левую часть уравнения f(x)=0.

Например, для решения уравнения 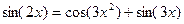для начального приближения 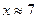нужно выполнить следующие команды:

Фрагмент программы   deff('y=F(x)', 'y=sin(2*x)-cos(3*x.^2)-sin(3*x)')root=fsolve(7,F)disp(root)

Результат   6.9755674

Для решения полиномиальных уравнений вида 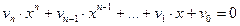используется функция

roots(a),

где а – вектор коэффициентов перед неизвестными полинома размерностью n+1(n – порядок полинома).

Результатом работы этой функции будет вектор корней полинома размерностью n.

Пример решения полиномиального уравнения 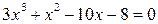приведен ниже.

Фрагмент программы   v=[3 1 -10 -8]R=roots(v)disp(R)

Результат   2. - 1.3333333 - 1.

Для уравнения 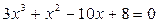два корня – комплексные.

Фрагмент программы v=[3 1 -10 8]R=roots(v)disp(R)

Результат - 2.2935835 0.9801251 + 0.4494650i 0.9801251 - 0.4494650i

Функция rootsможет также принимать в качестве параметра полином, созданный функциейpolyи представляющий собой левую часть уравнения :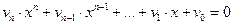

Poly(a, x, f1 ),

где a –вектор коэффициентов полинома записанных в обратном порядке, x - символьная переменная, f1– символьная переменная, принимающая значения 'c' или 'r' (roots или coeff).

Например, чтобы создать полином 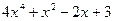, нужно использовать команду

Фрагмент программы p=poly([3 -2 1 0 4],'x','c')disp(p)

Результат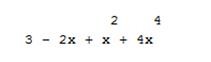

Для решения уравнения 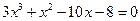можно выполнить следующие команды:

Фрагмент программы p=poly([-8 -10 1 3],'x','c')R=roots(p)disp(R)

Результат 2. - 1.3333333 - 1.

Для решения систем линейных уравнений в Scilab есть следующие способы:

- применение операции левого матричного деления;

- использование обратной матрицы.

Если задана система линейных алгебраических уравнений вида:

AX=B,

где А – матрица коэффициентов перед неизвестными системы, В – вектор свободных членов, то решение системы может быть найдено в виде:

Х=А \ B

То же самое решение может быть получено с помощью обратной матрицы, например:

X=inv(A)*B

Например, решить систему уравнений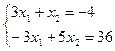

можно так:

Фрагмент программы A=[3 1;-3 5]; B=[-4 ;36]; X=inv(A)*B, disp(X)или X1=A\B , disp(X1)

Результат - 3.1111111 5.3333333

Для решения систем нелинейных уравнений можно использовать функцию

Fsolve(x0,f),

где x0 –вектор начальных приближений для неизвестных, f –функция, определяющая систему

Например, решение системы 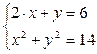можно выполнить следующим образом:

Фрагмент программы function [y]=fun(x) y(1)=2*x(1)+x(2)-6 y(2)=x(1)^2+x(2)^2-14endfunctionX0=[1;1]R=fsolve(X0,fun)disp(R)

Результат 1.2338096 3.5323808

Практическая часть

Задание 1. Вычисление определенного интеграла

Постановка задачи. Вычислить числовое значение интеграла от этой функции в заданных пределах интегрирования методом трапеций, методом квадратурных формул и с помощью функции intg.

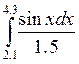
Шаг 1. Создадим вектор X, значения которого будут изменяться от 2,1 до 4,3 с шагом 0.01.

Шаг 2. Создадим вектор Y, каждое значение которого вычисляется по формуле .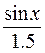

Шаг 3. Применим команду inttrap(X, Y).

Шаг 4. Используем функцию integrate,задав подынтегральную функцию в символьном виде.

Шаг 5. Определим внешнюю функцию с помощью команды deffили конструкции function

Шаг 6. Выведем результаты, используя команду disp.

Программа	Результат выполнения
X =2.1:0.01:4.3 Y =sin(X)/1.5 integral_1 = inttrap(X,Y)integral_2=integrate('sin(x)/1.5', 'x', 2.1, 4.3)disp(integral_1)disp(integral_2)	- 0.0693640 - 0.0693646
deff('y=F(x)','y=sin(x)/1.5'); integral_3=intg(2.1,4.3,F)function y=f(x) y=sin(x)/1.5endfunctionintegral_4=intg(2.1,4.3,f)disp(integral_3)disp(integral_4)	- 0.0693646 - 0.0693646

Индивидуальные задания приведены в таблице 3.4.

Таблица 3.4

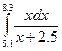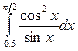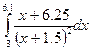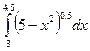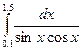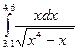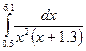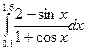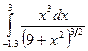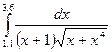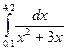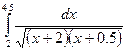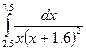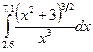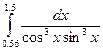Задание 2. Поиск корней уравнения, графическая интерпретация

Постановка задачи. Найти корень уравнения для заданного начального приближения. Выполнить графическую интерпретацию результата.

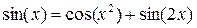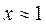Шаг 1. Определим внешнюю функцию с помощью команды deffили конструкции function

Шаг 2. Найдем корень уравнения с помощью функции fsolve,подставив в качестве первого параметра заданное начальное приближение.

Шаг 3. Выведем результат, используя команду disp.

Шаг 4. Выполним графическую интерпретацию результата. Для этого зададим аргумент функции из левой части уравнения таким образом, чтобы найденный корень попадал в диапазон между первым и последним элементом вектора. Построим график функции из левой части уравнения с помощью plot.Построим также линию y=0 и отметим точку с абсциссой, равной корню, и ординатой, равной значению функции для корня.

Программа	Результат выполнения
deff('y=F(x)', …'y=sin(x)-cos(x.^2)-sin(2*x)')root=fsolve(1,F)disp(root)x=0.5:0.01:2.5plot(x,F(x),'-b',root,F(root),'xr',x,0,'-k')	1.1695683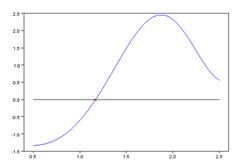

Индивидуальные задания приведены в таблице 3.5

Таблица 3.5

Вариант	Уравнение	Начальное приближение
1.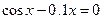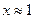
2.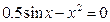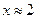
3.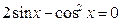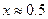
4.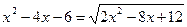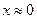
5.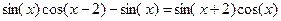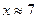
6.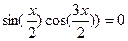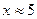
7.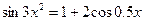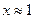
8.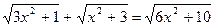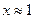
9.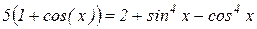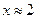
10.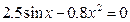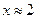
11.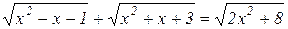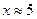
12.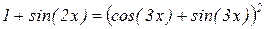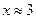
13.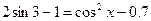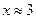
14.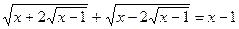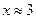
15.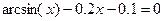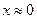

Задание 3. Поиск корней полиномиального уравнения, графическая интерпретация

Постановка задачи. Найти все корни полиномиального уравнения. Выполнить графическую интерпретацию для одного из найденных действительных корней.

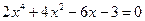
Шаг 1. Создадим вектор коэффициентов полинома в левой части уравнения (или полином с помощью poly)

Шаг 2. Найдем корни уравнения с помощью функции roots.

Шаг 3. Выведем результат, используя команду disp.

Шаг 4. Выполним графическую интерпретацию результата. Для этого зададим аргумент функции из левой части уравнения таким образом, чтобы выбранный действительный корень попадал в диапазон между первым и последним элементом вектора. Построим график функции из левой части уравнения с помощью plot.Построим также линию y=0 и отметим точку с абсциссой, равной корню, и ординатой, равной значению функции для корня.

Программа	Результат выполнения
v=[2 0 4 -6 -3]R=roots(v)disp(R)root=R(3)x=0.5:0.01:2y=2*x.^4+4*x.^2-6*x-3F_root=2*root^4+4*root^2-6*root-3plot(x,y,'-b',root,F_root,'xr',x,0,'-k')	- 0.4129576 + 1.7282075i - 0.4129576 - 1.7282075i 1.2164706 - 0.3905555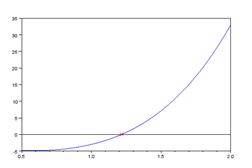

Индивидуальные задания приведены в таблице 3.6.

Таблица 3.6

Вариант	Уравнение
1.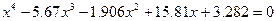
2.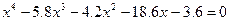
3.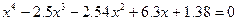
4.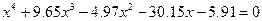
5.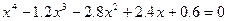
6.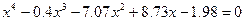
7.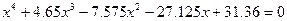
8.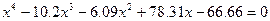
9.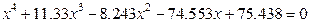
10.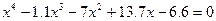
11.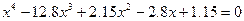
12.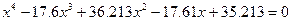
13.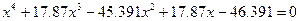
14.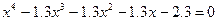
15.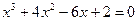

Задание 4. Решение системы линейных уравнений

Постановка задачи. Решить систему линейных уравнений.

Шаг 1. Создадим матрицу коэффициентов при неизвестных

Шаг 2. Создадим вектор свободных членов.

Шаг 3. Умножим матрицу, обратную к матрице коэффициентов, на вектор свободных членов (или применим операцию левого матричного деления).

Шаг 4. Выведем результат, используя команду disp.

Программа	Результат выполнения
A=[3 1 1;-3 5 6;1 -4 -2]; B=[-4 ;36;-19]; X=inv(A)*B disp(X)	- 3. 3. 2.

Индивидуальные задания приведены в таблице 3.7.

Таблица 3.7

№	Система уравнений	№	Система уравнений
1.		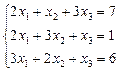2.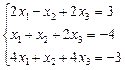
3.		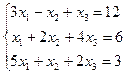4.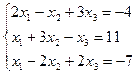
5.		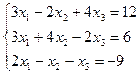6.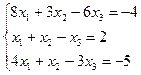
7.		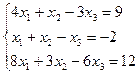8.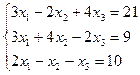
9.		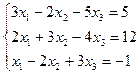10.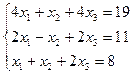
11.		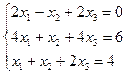12.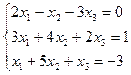
13.		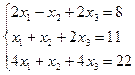14.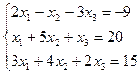
15.		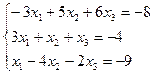16.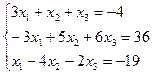