Сведения, необходимые для выполнения работы.

Министерство образования и науки Российской Федерации

Федеральное государственное автономное образовательное учреждение

высшего профессионального образования

«Национальный исследовательский ядерный университет «МИФИ»

Волгодонский инженерно-технический институт – филиал НИЯУ МИФИ

МЕТРОЛОГИЯ

Методические указания

к лабораторным работам

Волгодонск 2012

Методические указания к лабораторным работам предназначены для студентов дневной, вечерней и заочной форм обучения специальностей 14020465 «Электрические станции», 23020165 «Информационные и управляющие системы», 14140365 «Атомные станции: проектирование, эксплуатация и инжиниринг», 22030165 «Автоматизация технологических процессов и производств (по отраслям)», а также направлений подготовки бакалавров 14010062 «Теплоэнергетика и теплотехника», 23040062 «Информационные системы и технологии», 14040062 «Электроэнергетика и электротехника», 14070062 «Ядерная энергетика и теплофизика».

Содержание

Работа 1.1. Прямые и косвенные однократные измерения…………………………………………………4

Работа 1.2. Обработка и представление результатов однократных измерений при наличии систематической погрешности ………………………………………………………………………………………………8

Работа 1.3. Стандартная обработка результатов прямых измерений с многократными наблюдениями..13

Работа 2.1. Определение погрешности цифрового вольтметра методом прямых измерений ……………19

Работа 4.1. Терморезисторные измерительные преобразователи. Измерение температуры…………….23

Работа 1.1. Прямые и косвенные однократные измерения

Цель работы:

1. Приобретение навыков планирования и выполнения прямых и косвенных одно­кратных измерений.

2. Получение опыта по выбору средств измерений, обеспечи­вающих решение поставленной измерительной задачи.

3. Изучение способов обработ­ки и правильного представления результатов прямых и косвенных однократных измерений.

Сведения, необходимые для выполнения работы.

Подавляющее большинство измерений, выполняемых на практике, являются однократными. Прежде чем выполнить однократное измерение, необходимо вы­брать средство измерения. При выборе средства измерения, исходя из представ­ления об условиях проведения измерения, о свойствах измеряемой величины и ее примерном значении, а также о необходимой точности измерения, определяют с помощью какого измерительного прибора, какого типа, какого класса точности, на каком пределе шкалы будет лучше проводить измерение. Если об ожидаемом значении измеряемой величины можно судить только с большой неопределенно­стью, средство измерения выбирают предварительно, устанавливают для него наиболее подходящий предел шкалы и проводят пробные измерения, после чего средство измерения и предел шкалы выбирают окончательно и выполняют изме­рение для получения результата.

За результат однократного измерения принимают показания средства измере­ния. Результирующая погрешность однократного измерения в общем случае за­висит от целого ряда факторов, в частности от инструментальной и методической составляющих погрешности, от влияния внешних воздействий и т. д. На практике однократные измерения всегда стремятся организовать так, чтобы результирую­щая погрешность определялась в первую очередь инструментальной составляю­щей погрешности. В таком случае погрешность измерений оценивают, исходя из класса точности выбранного средства измерений (см. приложение 1).

При расчете погрешности на основе данных о классе точности средства изме­рений зачастую получают значения, содержащие большое число десятичных зна­ков. Отметим, что исходными данными для расчета всегда являются нормируе­мые значения погрешности средства измерений, которые указываются с одной или двумя значащими цифрами. Отсюда следует, что в окончательном значении рассчитанной погрешности должны быть оставлены только первые одна-две зна­чащие цифры. Действительно, если полученное значение погрешности начинает­ся с цифр 1 или 2, то, отбросив второй знак, можно получить большую ошибку (до 30-50%), если же значение погрешности начинается, например, с цифры 9, то ука­зание погрешности, например, 0,94 вместо 0,9 является дезинформацией, так как исходные данные не обеспечивают такой точности.

Поэтому при выполнении расчетов следует руководствоваться следующей ре­комендацией [9]:

· если полученное при расчете значение погрешности начинается с цифры, равной или большей, чем 3, то в нем сохраняется лишь один знак;

· если полученное значение начинается с цифр, меньших 3, то есть с цифр 1 или 2, то в нем сохраняют два знака.

В соответствии с этим правилом устанавливают­ся и нормируемые значения погрешностей средств измерений: в числах 1,5 и 2,5 % указывают два знака, но в числах 0,5; 4; 6 % указывается только один знак.

С учетом изложенного можно сформулировать следующие три правила округ­ления рассчитанного значения погрешности и полученного экспериментального результата измерения.

Погрешность результата измерения указывается двумя значащими цифра­ми, если первая из них равна 1 или 2, и одной - если первая цифра есть 3 и более.

Результат измерения округляется до того же десятичного разряда, которым заканчивается округленное значение абсолютной погрешности.

Округление производится лишь в окончательном ответе, а все промежуточ­ные вычисления проводят с одной-двумя лишними значащими цифрами.

Пример. Вольтметр класса 2,5 с пределом шкалы 300 В показал напряжение U_x=267,5 В. Оценить погрешность однократного измерения.

Решение. Класс точности задан приведенной погрешностью γ=2,5%. Абсолютная погрешность измерения равна 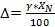= 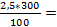7,5 В≈8 В. Относительная погрешность измерения равна 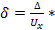100%= 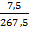*100%=2,81% ≈ 2,8%.

Таким образом, в окончательном ответе следует указать: «Абсолютная по­грешность измерения составляет 8 В, относительная погрешность измерения со­ставляет 2,8%, измеренное напряжение Ux = 268±8 В». Более наглядно результат измерений можно представить в виде 260 В < Ux < 276 В.

При проведении однократных измерений всегда стремятся поддерживать нор­мальные условия и выбрать такой способ измерений, чтобы методическая по­грешность и субъективные погрешности оказывали минимальное воздействие на результат. Если, тем не менее, условия измерений отличаются от нормальных, в результаты измерений вносят поправки, учитывающие погрешности, обуслов­ленные воздействием влияющих величин. При выполнении данной работы следу­ет предполагать, что условия измерений нормальные, а методические и субъек­тивные погрешности пренебрежимо малы.

При проведении косвенных измерений погрешность определяется по резуль­татам прямых измерений. В общем случае решение этой задачи оказывается весь­ма сложным. Однако есть несколько случаев, когда оценить пределы погрешно­сти результата косвенного измерения просто:

1. Измеряется величина Z, связанная зависимостью Z = X ± Y. Величины X и Y измерены с абсолютными погрешностями ΔX и ΔY, соответственно. В этом случае для оценки предела абсолютной погрешности результа­та составляющие погрешности суммируются без учета знака, а именно: ΔZ = ΔX + ΔY.

2. Измеряется величина Z, связанная зависимостями Z = X•Y или Z = X/Y. Величины X и Y измерены с абсолютными погрешностями ΔX и ΔY, соот­ветственно. В этом случае для оценки предела относительной погрешности результата составляющие относительные погрешности суммируются без учета знака, а именно: δZ = δX + δY.

3. Измеряется величина Z, связанная зависимостью Z = F(X, Y). Величины X и Y измерены с абсолютными погрешностями ΔX и ΔY соответственно. В этом случае для оценки предела абсолютной погрешности результат следует использовать выражение: ΔZ=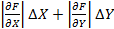

Легко видеть, что предыдущие формулы для погрешностей следуют из последнего, более об­щего соотношения. Использование этих правил позволяет получить удовлетворительную оценку предельной погрешности результата косвенного измерения, когда число аргумен­тов в функциональной зависимости не превышает четырех-пяти.

Отметим, что приведенные в пп. 1-3 способы оценки предельной погрешности косвенных измерений могут дать завышенную оценку значения результирующей погрешности. Однако с точки зрения достоверности результата измерения и с учетом простоты описанного способа такой подход оказывается, как правило, вполне приемлемым.