Связь глобальных и локальных номеров узлов

Координаты узловых точек, м

Номер узла	X	Y
		0.0275
		0.055
	0.02
	0.02	0.04
	0.04
	0.04	0.0125
	0.04	0.025
	0.07
	0.07	0.025
	0.1
	0.1	0.0125
	0.1	0.025

На рисунке 3 наглядно представлено это разбиение, выполненное в программе ProFEM.

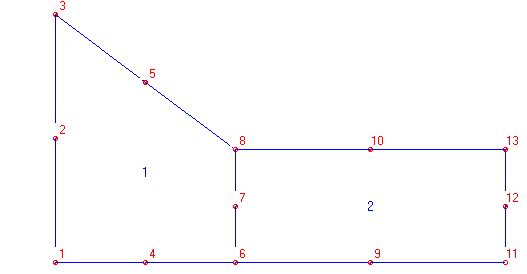
Рис.3 Вид фрагментов

Далее создаётся матрица связности фрагментов (таблица №2).

Таблица №2

Матрица связности элементов

Номер фрагмента	1-ая сторона	2-ая сторона	3-я сторона	4-ая сторона

Задаётся количество разбиений и локальные номера узлов в каждом фрагменте. Связь глобальных и локальных номеров узлов представлена в таблице №3:

Таблица №3

Связь глобальных и локальных номеров узлов

Номер фрагмента

На рис. 4 представлен результат работы программы для количества разбиений фрагмента равных 3 (x=h=3):

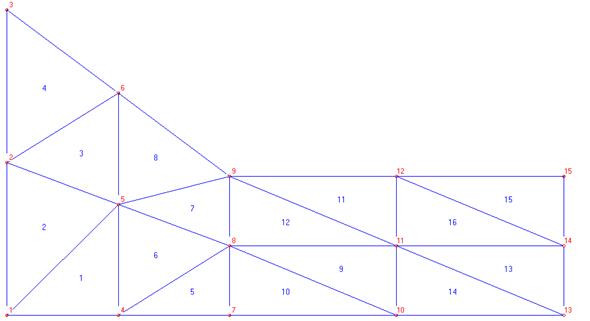
Рис. 4. Вид сетки для разбиения равного 3

при помощи программы выполняется расчёт напряжённо-деформированного состояния детали при заданных граничных условиях:

1. Вводится значение модуля упругости и коэффициент Пуассона (рис. 5):

Рис.5. Ввод значения модуля упругости и коэффициент Пуассона

2. Вводится информация о заданных силах и перемещениях (рис.6,7):

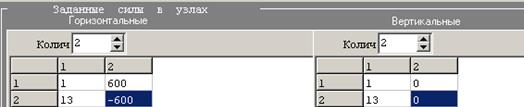
Рис.6. Задание горизонтальных и вертикальных сил в узлах

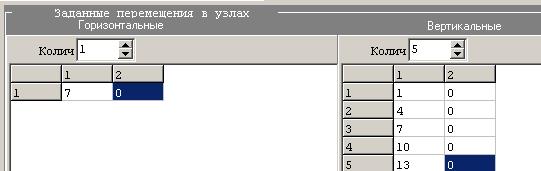
Рис.7 . Задание горизонтальных и вертикальных перемещений в узлах

3. Просмотр окна результатов решения поставленной задачи (рис. 8):

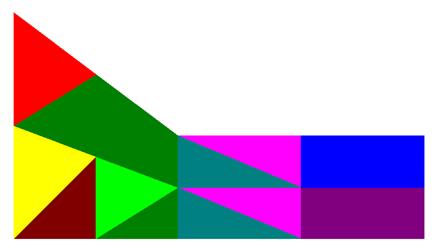
Рис.8. Распределение горизонтальных перемещений в детали для разбиения равного 3

По полученным результатам решения можно судить не только о перемещениях, но и о действующих напряжениях.

При необходимости полученные результаты можно посмотреть в получающейся таблице (рис. 9):

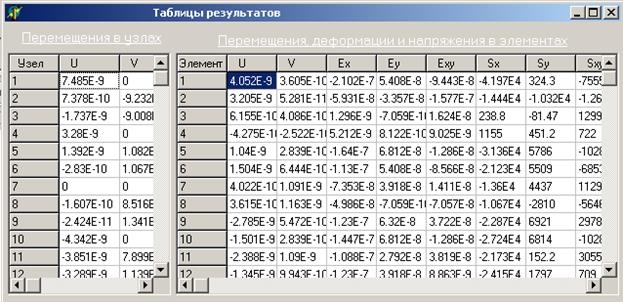
Рис.9.Численные значения горизонтальных и вертикальных перемещений в узлах; горизонтальных и вертикальных перемещений в элементах; горизонтальных, вертикальных и касательных перемещений в элементах; горизонтальных и вертикальных напряжений в элементах

Далее рассматривается решение задачи с большим количеством разбиений. Принимается разбиение равное 5, тогда сетка принимает следующий вид (рис. 10):

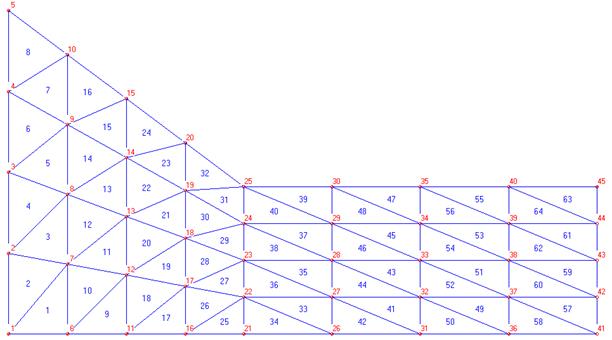
Рис.10. Вид сетки для разбиения равного 5

Решение в случае 5-ти разбиений (рис.11.):

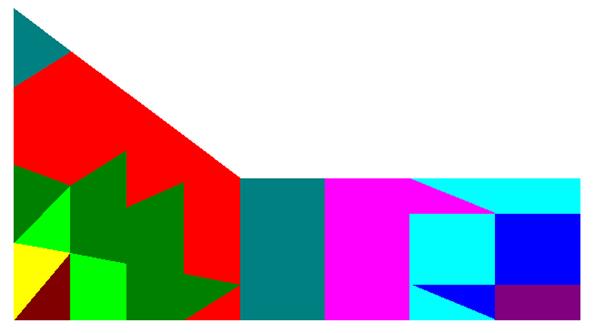
Рис.11. Распределение горизонтальных перемещений в детали для разбиения равного 5

Далее принимается разбиение равное 7, сетка принимает следующий вид (рис. 12):

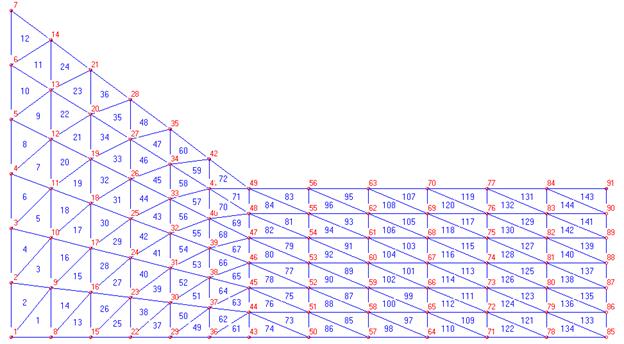
Рис.12. Вид сетки для разбиения равного 7

Решение в случае 7-ми разбиений (рис.13.):

Рис.13.Распределение горизонтальных перемещений в детали для разбиения равного 7

Если взять ещё большее разбиение, например 15, то картина распределения горизонтальных перемещений будет менее дискретной:

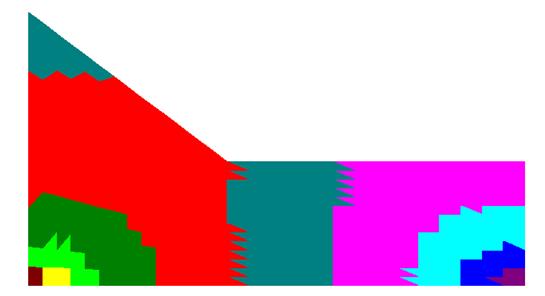
Рис.14. Распределение горизонтальных перемещений для разбиения равного 15

Построение графиков зависимости координат х узлов от величин горизонтальных перемещений u для всех трёх разбиений производится с помощью программы MathCad:

1. Задание матриц x₃, х₅, х_7, то есть координат х узлов в сечении ОХ на участке от 0 до 40 мм, расположенных на равных расстояниях:

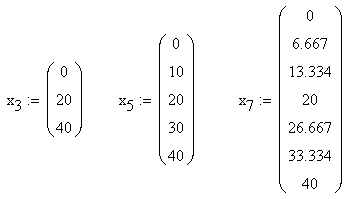
2. Задание матриц перемещений u₃, u₅, u₇ узлов:

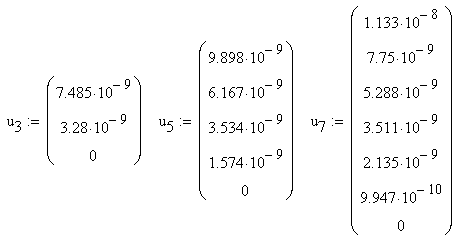
3. На рис. 15 представлен совмещённый график зависимостей координат х узлов в сечении ОХ на участке от 0 до 40 мм, расположенных на равных расстояниях, от величин горизонтальных перемещений u для трёх разбиений:

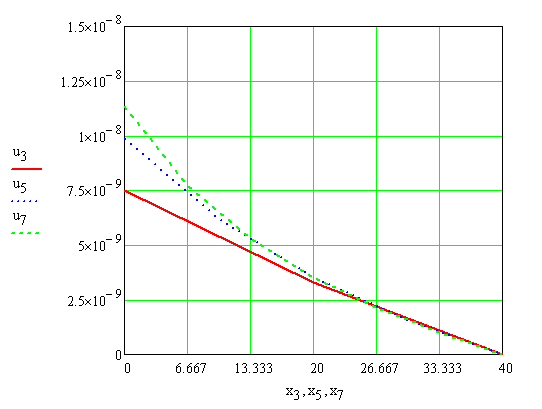
Рис.15. График зависимостей координат х узлов в сечении ОХ на участке от 0 до 40 мм, расположенных на равных расстояниях, от величин горизонтальных перемещений u для трёх разбиений

Вывод

Был изучен метод конечных элементов, также была решена плоская задача теории упругости с использованием с треугольных элементов с помощью программы ProFEM. Решение было выполнено с тремя разными количествами разбиений (3, 5 и 7 соответственно). В результате была получена зависимость координат х узлов от перемещений u в сечении ОХ на отрезке от 0 до 40мм для разбиений 3, 5 и 7; с увеличением величины разбиения решение приближается к точному.