Многие задачи на графах состоят в определении частей графа с заданными свойствами.

Часть графа называется подграфом графа

Если , а подмножество образовано только ребрами, инцидентными вершинам множества Е'.

Полным графом называется граф 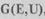, у которого каждая вер-

Рис. 1.9. Полный граф

шина 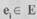соединена ребрами с остальными вершинами (рис. 1.9).

Маршрутом графа G называется последовательность ребер S = = (u₁, u₂, ... u_n), в которой каждые два соседних ребра имеют общую вершину, т.е. 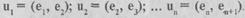Не исключено,

Что одно и то же ребро может встречаться несколько раз на одном маршруте.

Две вершины е₁ и е. называются связанными, если существует мар­шрут из е_i в е._j

Компонентой связности графа называется подмножество его вер­шин с инцидентными им ребрами, такое, что любая вершина свя­зана с любой другой вершиной маршрута, Например, из графа на рис. 1.10 можно выделить следующие две компоненты связанности, показанные сплошной линией.

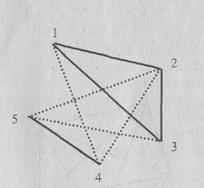
Рис. 1.10. Компоненты связанности графа

Простой цепью, или простым путем, называется маршрут, в ко­тором ни одно ребро не повторяется дважды. Элементарной цепью или элементарным путем называется маршрут, в котором ни одна верши­на не повторяется дважды. Циклом в графе называется маршрут, у которого начальная вершина совпадает с конечной. Например, следу­ющий граф имеет цикл S = (1, 2, 3, 5, 4, 1) (рис. 1.11).

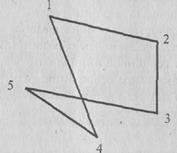
Рис. 1.11. Цикл в графе

Цикл, проходящий по всем ребрам графа только один раз, на­зывается эйлеровым циклом. В теории графов доказывается теорема, определяющая, содержит ли граф эйлеров цикл. Оказывается, конеч­ный граф содержит эйлеров цикл тогда и только тогда, когда он свя­зан, и все его локальные степени вершин четные. Важной приклад­ной задачей теории графов является задача поиска в графе цикла, проходящего через каждую вершину только один раз. Такие циклы называются гамильтоновыми циклами.

Весьма важным является связанный граф, не имеющий циклов, он называется деревом. В дереве любые две вершины связаны един­ственным путем. Вершина называется концевой, если ей инцидентно не более одного ребра; одна из концевых вершин может быть выбрана в качестве корня.

Задание графа

Граф может задаваться в виде рисунка, аналитически, в виде матрицы. Выше приводилось задание графа в виде рисунка. Анали­тическое задание состоит в задании элементов множества вершин 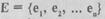и множества ребер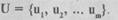

Для выполнения различного рода формальных преобразований над графами удобно использовать -их матричные задания. Матрица А размерностью n х n называется матрицей смежности графа ,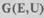

если ее элементы образованы по правилу: элемент матрицы если вершины е_i. и е_j. соединены m ребрами, и , если эти вершины не связаны ребрами. Матрица смежности имеет число строк и столбцов, равное количеству вершин графа.

Матрица А размерностью n х m называется матрицей инцидент­ности графа G(Е,U),если ее элементы образованы по правилу: элемент матрицы . если вершина е. инцидентна ребру 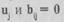в противном случае. Так как каждое ребро инцидентно двум вершинам, то в каждой строке этой матрицы ровно два ненулевых элемента.

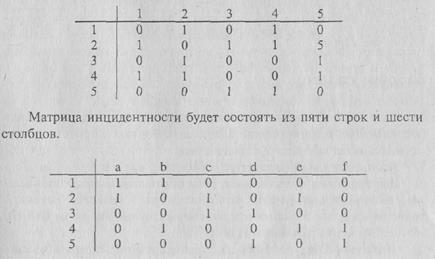
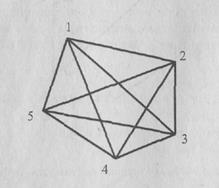
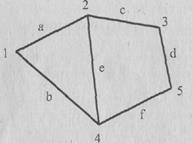Построим матрицы смежности и инцидентности для графа, изображенного на рис. 1.12.

Рис. 1.12. Пример графа Матрица смежности будет состоять из пяти строк и пяти столбцов.