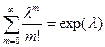По выполнению первого вопроса

ЗАДАНИЕ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ПРАКТИЧЕСКОМУ ЗАНЯТИЮ

По учебной дисциплине

Теория вероятностей и

математическая статистика»

Для студентов специальности

«Компьютерная безопасность»

Раздел1. Случайные события

Занятие 1.5.Числовые характеристики

Дискретных случайных величин.

Обсуждено и одобрено

на заседании кафедры

«Компьютерная безопасность»

Протокол №____от________2007 г.

Учебные и воспитательные цели:

В результате настоящего занятия и последующей самостоятельной работы Вам необходимо:

1. Изучить числовые характеристики дискретных случайных величин и их свойства.

2. Используя формулы числовые характеристики дискретных случайных величин уметь определять математическое ожидание и дисперсию.

3. Выработать навыки в использовании формул математического ожидания и дисперсии.

4. Приобрести навыки в проведении математических расчётов.

Время80 минут

Распределение времени занятия:

Вступительная часть - 5 мин

Проверка готовности студентов к занятию - 5 мин

Учебные вопросы занятия:

1. Математическое ожидание дискретной случайной величины - 40 мин

2. Дисперсия дискретной случайной величины - 30 мин

3. Заключение - 3 мин

4. Задание студентам для самостоятельной работы - 2мин

СОДЕРЖАНИЕ ЗАНЯТИЯ

Вступительная часть

На сегодняшнем практическом занятии Вам предлагается выполнить практические задания, связанные с нахождением числовых характеристик дискретных случайных величин.

Проверка готовности студентов к занятию

1. Дать определение случайной величины.

2. Какая случайная величина называется дискретной?

3. Что называется математическим ожиданием?

4. Дать определение дисперсии дискретной случайной величины?

5. дать определение среднего квадратического отклонения?

Методические пояснения и рекомендации

по выполнению первого вопроса.

1.Дискретная случайная величина Х задана законом распределения

А)

Х
р	0,2	0,1	0,4	0,3

Б)

Х
р	0,3	0,1	0,2	0,2

В)

Х
р	0,1	0,7	0,2

Вычислить математическое ожидание.

2.Найти математическое ожидание дискретной случайной величины Z, если известны математические ожидания X и Y: а) Z=X+2Y, M(X)=5, M(Y)=3; б) Z=3X+4Y, M(X)=2, M(Y)=6.

3.Дискретная случайная величина Х принимает три возможных значения x 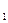=4 с вероятностью p 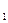=0.5; x 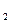=6 с вероятностью p 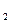= 0.3; x 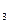с вероятностью p 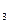. Найти x 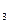и p , зная, что M(X)=8.

4.Контрольная работа состоит из трёх вопросов. На каждый вопрос приведено по 4 ответа. Составить и изобразить графически закон распределения числа правильных ответов при простом угадывании. Найти математическое ожидание этой случайной величины.

5.В билете 3 задачи. Вероятность правильного решения первой задачи равна 0,9, второй – 0,8, третьей – 0,7. Составить и изобразить графически закон распределения числа правильного решения задач в билете и вычислить математическое ожидание этой случайной величины.

6.Сделано два высокорисковых вклада: 10 тыс. рублей в компанию А и 15 тыс. рублей в компанию В. Компания А обещает 50% годовых, но может лопнуть с вероятностью 0,2. Компания В – 40% годовых, но может лопнуть с вероятностью 0,15. Составить закон распределения случайной величины – общей суммы прибыли (убытка), полученной от двух компаний через год. Найти её математическое ожидание.

7.Найти математическое ожидание лотерейных билетов, на которых выпадут выигрыши, если приобретено 20 билетов, при чём вероятность выигрыша по одному билету составляет 0,3.

8.Найти математическое ожидание дискретной случайной величины Х, распределённой по закону Пуассона:

X	0	1	2	k
p	exp(-λ)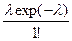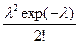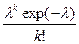

Учитывать, что