Перевод двоичных чисел в восьмеричную и шестнадцатеричную системы счисления
Перевод двоичного числа в восьмеричную и шестнадцатеричную системы осуществляется также просто: двоичное число разбивается вправо и влево от точки, отделяющей целую часть от дробной, на триады (для восьмеричной системы счисления) или тетрады (для шестнадцатеричной системы счисления). При необходимости крайнюю левую триаду (тетраду) целой части и крайнюю правую (дробной части) дополняют нулями, а затем каждую триаду (тетраду) заменяют восьмеричной (шестнадцатеричной) цифрой.
Разобрать пример преобразования числа 10101011111101.1101001(2) в указанные системы счисления. Помните, что двоичное число разбивается вправо и влево от точки, отделяющей целую часть от дробной, на триады (для восьмеричной системы счисления) или тетрады (для шестнадцатеричной системы счисления). При необходимости крайнюю левую триаду (тетраду) целой части и крайнюю правую (дробной части) дополняют нулями, а затем каждую триаду (тетраду) заменяют восьмеричной (шестнадцатеричной) цифрой.
| Направление разбиения целой части на триады | Направление разбиения дробной части на триады ® | |||||||||||
| Исходное число | (0)10 | 101. | 1(00) | |||||||||
| ¯ | ¯ | ¯ | ¯ | ¯ | ¯ | ¯ | ¯ | |||||
| Цифры 8 с.с. | ||||||||||||
| Результат: | 25375.644(8) | |||||||||||
| Направление разбиения целой части на тетрады | Направление разбиения дробной части на тетрады ® | |||||||||||
| Исходное число | (00)10 | 1101. | 001(0) | |||||||||
| ¯ | ¯ | ¯ | ¯ | ¯ | ¯ | |||||||
| Цифры 16 с.с. | A | F | D | D | ||||||||
| Результат: | 2AFD.D2(16) | |||||||||||
Задание 4 Самостоятельно переведите числа полученные в результате расчетов выполненных согласно задания 1 в восьмеричную и шестнадцатеричную системы счисления. Реультаты сравнить с исходными числами, представленными в восьмеричной и шестнадцатеричной системах счисления
Арифметические операции в в ЭВМ Операции с фиксированной точкой.
Представление целых чисел без знака.
В форме с фиксированной точкой все числа изображаются в виде последовательности цифр с постоянным для всех чисел положением точки, отделяющей целую часть от дробной.
Эта форма наиболее проста, естественна, но имеет небольшой диапазон представления чисел и поэтому используется как вспомогательная и только для целых чисел.
Целые числа могут представляться в компьютере со знаком или без знака.
Целые числа без знака обычно занимают в памяти один или два байта и принимают значения из диапазона, представленного в табл. 1.
Таблица 2. Диапазоны значений целых чисел без знака
| Формат числа в байтах | Диапазон | |||
| Запись с порядком | Обычная (десятичная) запись | Двоичная запись | Шестнадцатеричная запись | |
| 0 ... 28–1 | 0 ... 255 | 00000000 … 11111111 | 00 … FF | |
| 0 ... 216–1 | 0 ... 65535 | 0000000000000000 … 1111111111111111 | 0000 … FFFF |
Пример1. Представление числа 72(10) = 1001000(2) в однобайтовом и двухбайтовом форматах:
| Номера разрядов | Номера разрядов | ||||||||||||||||||||||||
| Биты числа | Биты числа |
Задание 5.
Запишите в виде таблицы, согласно примеру №1, ваш порядковый номер в журнале учета студентов в однобайтовом и двухбайтовом форматах, предварительно преобразов этот номер в двоичную систему счисления.
5.2. Представление целых чисел со знаком
Целые числа со знаком обычно занимают в памяти компьютера один, два или четыре байта, при этом самый левый (старший) разряд содержит информацию о знаке числа. Знак «плюс (+)» кодируется нулем, а «минус (-)» — единицей.
Таблица 2. Диапазоны значений целых чисел со знаком
| Формат числа в байтах | Диапазон | ||
| Запись с порядком | Обычная (десятичная) запись | Шестнадцатеричная запись | |
| –27 ... 27–1 | –128 ... 127 | 80 … 7F | |
| –215 ... 215–1 | –32768 ... 32767 | 8000 … 7FFF | |
| –231 ... 231–1 | –2147483648 ... 2147483647 | 80000000 … 7FFFFFFF |
Рассмотрим особенности записи целых чисел со знаком на примере однобайтового формата, при котором для знака отводится один разряд, а для цифр абсолютной величины – семь разрядов.
В ЭВМ применяются три формы записи (кодирования) целых чисел со знаком: прямой код, обратный код, дополнительный код. Последние две формы применяются особенно широко, так как позволяют упростить конструкцию арифметико-логического устройства компьютера путем замены разнообразных арифметических операций операцией сложения.
Положительные числа в прямом, обратном и дополнительном кодах изображаются одинаково — двоичными кодами с цифрой 0 в знаковом разряде. Например:

Отрицательные числа в прямом, обратном и дополнительном кодах имеют разное изображение.
Прямой код отрицательного числа: в знаковый разряд помещается цифра 1, а в разряды цифровой части числа — двоичный код его абсолютной величины. Например:
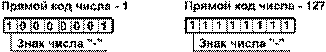
Обратный код отрицательного числа: получается инвертированием всех цифр двоичного кода абсолютной величины числа, включая разряд знака: нули заменяются единицами, а единицы — нулями. Например:

Дополнительный код отрицательного числа: получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду. Например:
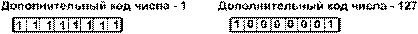
Обычно отрицательные десятичные числа при вводе в машину автоматически преобразуются в обратный или дополнительный двоичный код и в таком виде хранятся, перемещаются и участвуют в операциях. При выводе таких чисел из машины происходит обратное преобразование в отрицательные десятичные числа.
Задание 6.
Запишите в однобайтовом формате прямой, обратный и дополнительный коды четырех чисел, приведенных в таблице №3, выбрав их в строке согласно порядкового номера студента в журнале учета, предварительно преобразов эти числа в двоичную систему счисления.
Таблица №3
| Порядковый № | ||||||||
| -77 | -46 | |||||||
| -69 | -64 | |||||||
| -17 | -83 | |||||||
| -33 | -58 | |||||||
| -40 | -43 | |||||||
| -58 | -122 | |||||||
| -53 | -33 | |||||||
| -16 | -41 | |||||||
| -64 | -10 | |||||||
| -64 | -77 | |||||||
| -63 | -69 | |||||||
| -73 | -117 | |||||||
| -62 | -22 | |||||||
| -105 | -37 | |||||||
| -112 | -6 | |||||||
| -62 | -43 | |||||||
| -124 | -110 | |||||||
| -119 | -36 | |||||||
| -65 | -29 | |||||||
| -42 | -44 | |||||||
| -53 | -64 | |||||||
| -67 | -70 | |||||||
| -94 | -50 | |||||||
| -46 | -19 | |||||||
| -35 | -2 | |||||||
| -27 | -90 | |||||||
| -29 | -89 | |||||||
| -121 | -96 | |||||||
| -113 | -104 | |||||||
| -56 | -50 | |||||||
6. Арифметические действия над целыми числами.
6.1 Арифметические операции в двоичной системе счисления.
Разберите примеры сложения двух целых чисел без знаков. Помните, что при сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево.
Пример 2. Сложим числа 15 и 6 в различных системах счисления.
| Десятичная: 15(10)+6(10) | Двоичная: 1111(2)+110(2) 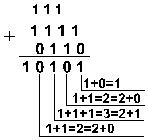 |
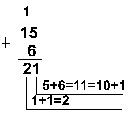 | |
| Ответ: 15+6 = 21(10) = 10101(2)) | |
| Проверка. Преобразуем полученные суммы к десятичному виду: 101012 = 24 + 22 + 20 = 16+4+1=21 |
Задание 7.
Самостоятельно сложите два целых положительных числа, выбранных из таблицы №3 (колонки 2 и 4), предварительно переведя их в двоичную систему счисления и осуществите проверку результата в десятичной системе.
