Эмпирическая модель расчета освещенности
При расчете освещенности граней применяют следующие типы освещения и отражения света от поверхностей.
§ Рассеянное
§ Диффузное
§ Зеркальное
Интенсивность освещения граней трехмерных объектов рассеянным светом считается постоянной в любой точке пространства. Она обусловлена множественными отражениями света от всех объектов в пространстве. При освещении трехмерного объекта рассеянным светом интенсивность отраженного света вычисляется как 
 , где
, где  - интенсивность падающего света,
- интенсивность падающего света,  - коэффициент рассеянного отражения, зависит от отражающих свойств материала грани.
- коэффициент рассеянного отражения, зависит от отражающих свойств материала грани.
Для расчета интенсивности диффузного отражения света может применяться закон косинусов Ламберта:  , где
, где 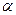 - угол падения, рассчитывается как угол между направлением на источник света и нормалью к поверхности. Пусть направление на источник света представлено единичным вектором
- угол падения, рассчитывается как угол между направлением на источник света и нормалью к поверхности. Пусть направление на источник света представлено единичным вектором  , а
, а  - единичный вектор нормали. Тогда
- единичный вектор нормали. Тогда  - скалярное произведение векторов. Тогда
- скалярное произведение векторов. Тогда  , где
, где  - коэффициент диффузного отражения.
- коэффициент диффузного отражения.
Вычисление зеркально отраженного света производится также с помощью различных эмпирических моделей, которые позволяют учитывать реальную шероховатость поверхностей. Например, в модели, предложенной Фонгом, интенсивность зеркально отраженного света рассчитывается в зависимости от степени отклонения от истинного значения вектора зеркально отраженного луча света. Пусть  - вектор зеркально отраженного луча света, а
- вектор зеркально отраженного луча света, а  - вектор, определяющий направление на наблюдателя. Тогда интенсивность зеркально отраженного света по модели Фонга рассчитывается так:
- вектор, определяющий направление на наблюдателя. Тогда интенсивность зеркально отраженного света по модели Фонга рассчитывается так:  , где
, где  - угол между векторами
- угол между векторами  и
и  . Константа n – может принимать значения от 1 до примерно 200, в зависимости от отражающей способности материала. Большим значениям n соответствует большая степень “гладкости” или “зеркальности” поверхности. Если векторы
. Константа n – может принимать значения от 1 до примерно 200, в зависимости от отражающей способности материала. Большим значениям n соответствует большая степень “гладкости” или “зеркальности” поверхности. Если векторы  и
и  - нормированы, то формула преобразуется к виду:
- нормированы, то формула преобразуется к виду:  .
.
Интенсивность отраженного света уменьшается обратно пропорционально квадрату расстояния от источника до наблюдателя. Поэтому можно записать формулу расчета интенсивности отраженного луча света для трех составляющих: рассеянного, диффузного и зеркального отражения с учетом расстояния:
 ,
,
где  - расстояние от точки отражения до наблюдателя, а
- расстояние от точки отражения до наблюдателя, а  - некоторая константа. Иногда, для ускорения вычислений, берут не вторую, а первую степень расстояния
- некоторая константа. Иногда, для ускорения вычислений, берут не вторую, а первую степень расстояния  .
.
В системах компьютерной визуализации также учитываются такие свойства материалов отражающих поверхностей как прозрачность, преломление и свечение. Степень прозрачности материала грани может описываться с помощью константы, принимающей значение от нуля до единицы, причем значение 1 соответствует полной непрозрачности материала грани. Пусть интенсивности отраженного света двух перекрывающихся поверхностей равны  и
и  . Пусть первая поверхность находится ближе к наблюдателю и является полупрозрачной с коэффициентом прозрачности
. Пусть первая поверхность находится ближе к наблюдателю и является полупрозрачной с коэффициентом прозрачности  . Тогда суммарная интенсивность отраженного света может быть вычислена как взвешенное среднее:
. Тогда суммарная интенсивность отраженного света может быть вычислена как взвешенное среднее:  .
.
Модели для вычисления эффектов преломления и свечения здесь не рассматриваются.
