По разработанным алгоритмам составить программы.

Лабораторная работа №1

Тема: Исследование временных характеристик алгоритмов.

Цель работы: Развитие умений и навыков теоретической и практической оценки временных характеристик алгоритмов.

Выполнение работы

Вариант 1.

Алгоритм линейного поиска. Вход: последовательность n чисел A=<a1,…,an> и число v. Выход: индекс i, для которого v=A[i] или NIL, если v не принадлежит А.

Использовать последовательный просмотр при поиске v. Оценить сколько сравнений потребуется алгоритму, если искомым может быть любой элемент массива А (с одинаковой вероятностью). Каково время работы в среднем и в худшем случае? Выразить это время Ө-обозначением. При поиске в отсортированном массиве можно сначала сравнивать искомый элемент со средним элементом массива и, узнав в какой из полученных частей массива находится искомый, продолжить поиск рекурсивно (двоичный поиск).

Написать программу двоичного поиска, учтя время на сортировку, с рекурсией. Определить её Ө.

Сравнить временные характеристики алгоритмов:

· линейного поиска,

· сортировки с двоичным поиском, представленными циклами,

· сортировки с двоичным поиском, представленными рекурсией.

Для заданных описаний задачи составить указанные алгоритмы ее решения.

Составим линейный алгоритм поиска

алг

нач

конст цел n:=4

цел i,v,j

целтаб A[1:n]

нц для i от 1 до n //вводим последовательность чисел

ввод A[i]

кц

ввод v // вводим с клавиатуры значение v

j:=0

нц для i от 1 до n // проверяем каждый элемент на совпадение с v

если A[i]=v то вывод i // если элемент равен v, то выводим его номер

иначе j:=j+1 // если нет, то увеличиваем счетчик элементом отличных от v

Все

кц

если j=n то вывод "NIL"

Все

кон

По разработанным алгоритмам составить программы.

Составим программу линейного поиска на языке С++

#include <iostream>

using namespace std;

int main()

{

int i,j=0,v;

const int n=100;

int A[n];

for (i=0; i<n; i++)

A[i]=rand()%10;

cin >> v;

for (i=0; i<n; i++)

if (A[i]==v) cout << i+1

else j++;

if (j==n) cout<<"NIL";

return 0;

}

Асимптотическая сложность алгоритма – O(n). Для списка из n элементов лучшим случаем будет тот, при котором искомое значение равно первому элементу списка и требуется только одно сравнение. Худший случай будет тогда, когда значения в списке нет (или оно находится в самом конце списка), в случае чего необходимо n сравнений.

Если искомое значение входит в список k раз и все вхождения равновероятны, то ожидаемое число сравнений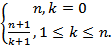

Например, если искомое значение встречается в списке один раз, и все вхождения равновероятны, то среднее число сравнений равно 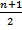. Однако, если известно, что оно встречается один раз, то достаточно n - 1 сравнений и среднее число сравнений будет равняться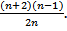

В любом случае, вычислительная сложность алгоритма O(n).