Поиск по заданному критерию

Программа поиска по заданному критерию может быть создана как усовершенст­вование программы поиска в ширину. Поиск по заданному критерию также начина­ется от начального узла, и в процессе его происходит сопровождение информации о множестве возможных путей. При поиске в ширину для продолжения всегда выби­рается кратчайший возможный путь (т.е. путь через наименее глубокие концевые узлы, достигнутые в ходе поиска), а в программе поиска по заданному критерию применяется усовершенствованный вариант этого принципа: определяется эвристи­ческая оценка для каждого возможного узла и для продолжения пути в соответствии с этой оценкой выбирается наилучший возможный узел.

В дальнейшем предполагается, что функция стоимости определена для дуг в про­странстве состояний, а с(п,п') — это стоимость перемещения от узла п к его пре­емнику п ' в пространстве состояний.

Допустим, что для эвристической оценки применяется функция £, такая, что для каждого узла п в пространстве состояний функция f {п} служит для оценки "сложности достижения" п. Б соответствии с этим наиболее перспективным из всех текущих возможных узлов является тот, для которого значение функции f становит-

ся минимальным. В настоящей главе применяется сформированная особым образом функция f, которая дает возможность использовать широко известный алгоритм А*. Функция f (n) будет сформирована таким образом, чтобы она оценивала стоимость наилучшего пути решения от начального узла з до целевого узла, при том условии, что этот путь пройдет через узел п. Предположим, что такой путь имеется, и целе­вым узлом, для которого стоимость этого пути становится минимальной, является узел t. Б таком случае оценку f (п) можно сформировать как сумму двух тернов (рис. 12.1) следующим образом: f<n)=g(n) + h(n)

где g (n) — оценка стоимости оптимального пути от s до n, a h [п.) — оценка стоимо­сти оптимального пути от п до t.

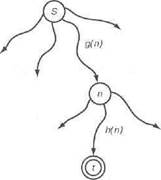Рис, 12,1. Формирование эври­стической оценка f(n) стои­мости пути с наименьшей

стоимостью от s до t через п: f(n} = g(n) + h (n)

После обнаружения узла п в процессе поиска возникает следующая ситуация: путь от з до п уже должен быть найден и его стоимость может быть вычислена как сумма стоимости дуг в этом пути. Такой путь от s до г не обязательно должен быть оптимальным (может существовать лучший путь от s до п, еще не обнаруженный в этом процессе поиска), но стоимость найденного пути, выраженная первым термом g (n), может служить в качестве оценки минимальной стоимости пути от s до п. За­дача определения второго терма, h(n! , сложнее, поскольку "мир" между узлами п и t к этому времени еще не был исследован в процессе поиска. Поэтому h \r\';. , как пра­вило, представляет собой в полном смысле слова эвристическую гипотезу, основан­ную на имеющейся в распоряжении алгоритма общей информации о данной кон­кретной задаче. Поскольку значение h зависит от проблемной области, универсально­го метода формирования функции h не существует. Конкретные примеры того, как могут выдвигаться подобные эвристические гипотезы, будут приведены ниже. Но на данный момент предположим, что функция h задана, и сосредоточимся на изучении программы поиска по заданному критерию.

Работу программы поиска по заданному критерию можно представить себе сле­дующим образом. Процесс поиска состоит и» множества конкурирующих подпроцес­сов, каждый из которых исследует свой собственный вариант; иными словами, ис­следует собственное поддерево. В поддеревьях имеются свои поддеревья; они иссле­дуются подпроцессами подпроцессов и т.д. Среди всех этих конкурирующих процессов в любой момент времени активным является только один — тот, который имеет дело с вариантом, являющимся в данный момент наиболее перспективным; таковым называется вариант с наименьшим значением функции f (или кратко

248 Часть I!.Применение языка Prolog в области искусственного интеллекта

{■значением), Остальные процессы должны находиться в состоянии ожидания до тех пор, пока текущие f-оценки не изменятся таким образом, что более перспективным станет какой-то иной вариант. После этого активность переключается на этот вари­ант. Можно представить себе, что такой механизм активизации и перехода в неак­тивное состояние действует следующим образом: процессу, работающему над вариан­том, имеющим в настоящее время наивысший приоритет, выделяются некоторые ре­сурсы и процесс остается активным до тех пор, пока эти ресурсы не будут исчерпаны. В этот период активности процесс продолжает развертывать свое подде­рево и сообщает решение, если был обнаружен целевой узел. Ресурсы для этого этапа выполнения выделяются на основании эвристической оценки ближайшего конкури­рующего варианта.

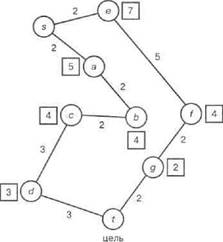
Пример такого поведения показан на рис. 12.2. Предположим, что дана некоторая дорожная карта и задача состоит в том, чтобы найти кратчайший маршрут между начальным городом з и целевым городом Z- В процессе оценки стоимости оставшего­ся расстояния в маршруте от города X до цели используется расстояние по прямой, обозначенное как disc ( X, t). Поэтому справедлива следующая формула: f(X) = g(X) + h(x) = g(X} + diat( X, t)

В данном примере можно представить себе, что поиск по заданному критерию со­стоит из двух процессов, в каждом из которых исследуется один из двух возможных путей: в процессе 1 — путь через узел а, в процессе 2 — путь через узел е. На на­чальных этапах процесс 1 является более активным, поскольку f-значения вдоль его пути меньше, чем вдоль другого пути. А в тот момент, когда процесс 1 находится в узле с, а процесс 2 — все еще в узле е, ситуация изменяется следующим образом:

f(c) - д(с) + h(e) = & + 4 = ",0 f(e) = g(e) + h(e) = 2 + 7 = Э

Поэтому f (e] < f <cj, и теперь процесс 2 переходит к узлу £, а процесс 1 ожида­ет. Но здесь возникает такая ситуация:

f(f) = 7 + 4 = 11 f(c) = 10 f(c) < f(f)

Поэтому процесс 2 останавливается, а процесс 1 получает разрешение продолжить свою работу, но только до пункта d, когда обнаруживается, что f (d) = 12 > ] 1. Те­перь процесс 2, активизированный в этот момент, беспрепятственно достигает цели t.

В процессе поиска, организованном таким образом, начиная с начального узла продолжается выработка новых узлов-преемников и путь всегда продлевается в наи­более перспективном направлении в соответствии с f-значения ми. В течение этого про­цесса формируется дерево поиска, корнем которого является начальный узел поиска. Поэтому рассматриваемая программа поиска по заданному критерию продолжает раз­вертывать дерево поиска до тех пор, пока не будет найдено решение. Такое дерево представлено в данной программе с помощью термов в двух описанных ниже формах.

1. Терм 1( N, »■/(.■;; представляет отдельный узел дерева (лист); где N - узел в пространстве состояний, G - значение функции g{W, (стоимость пути, прой­денного от начального узла до N), F — значение функции f(N) = G + h(N).

2. Терм t ( H, F/G, Subs) представляет дерево с непустыми поддеревьями; где N — корень дерева, Subs — список его поддеревьев, G — значение функции g (N), Е - "обновленное" f-значение И (под этим подразумевается f-значение наиболее перспективного преемника К); список Subs упорядочен в соответст­вии с возрастающими f-зпачения ми поддеревьев.

Например, снова рассмотрим процесс поиска, проиллюстрированный на рис. 12.2. В тот момент, когда был развернут узел а, дерево поиска состояло из трех узлов: корня s и двух его дочерних узлов, а и е. В рассматриваемой программе такое дере­во поиска представлено следующим термом: t( s, 7/0, [1 [а, 7/2), 1 (е,Э/2>:>

Глава 12. Эвристический поиск по заданному критерию

■V

<M = 2 + 5 = 7 la

4+4 = 8

6 + 4=1

9 + 3 =

<(в) = 2 + 7 = 9

7 + 4=11

9 + 2 = 11

11 +0 = 11

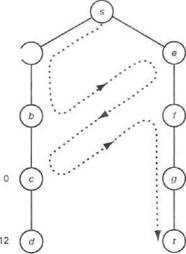
Рис.122 Поиск кратчайшего маршрута от s до t покарте: а) карта, на которой указаны расстояния меж­ду городами; чи-ела в квадратах указывают расстояние по прямой до I; б) порядок, в котором происходит изу­чение карты при поиске по заданному критерию. При определении эвристических оценок so основу взяты рас­стояния по прямой.Пунктирная линия показывает, как происходит переключение активности между аль­тернативными путями. Сплошная линия показывает упорядочение узлов о соответствии с их {значениями, иными словами, порядок, в котором узлы развертыва­лись (а не порядок, в котором они формировались)

Здесь f-значениекорня s равно 7, т.е. соответствует f-значениюнаиболее пер­спективного преемника корня — узла а. Теперь дерево поиска развертывается путем

Часть И. Применение языка Prolog в области искусственного интеллекта

развертывания наиболее перспективного поддерева а. Ближайшим конкурентом узла а является е, для которого f-значение равно 9. Таким образом, узлу а разрешено развернуться, при условии, что f-значение а не будеть превышать 9. Поэтому форми­руются узлы b и с. Значение f (с) = 10, поэтому предел развертывания превышен и варианту а больше не разрешено расти. В данный момент дерево поиска имеет сле­дующий вид: t( s, 9/0, [l(e,S/2), t[a, 10/2, [t<b,10/4, [He, 10/6)] > ] ) ] )

Следует отметить, что теперь f-значение узла а равно 10, а узла s — 9. Эти значе­ния обновлены в связи с тем, что были сформированы новые узлы, о и с. В настоя­щее время наиболее перспективным преемником узла s является е, для которого f-значение равно 9.

Обновление 1 -значенийнеобходимо для того, чтобы программа имела возможность распознавать на каждом уровне дерева поиска наиболее перспективное поддерево (т.е. дерево, которое содержит наиболее перспективный концевой узел). Такая моди­фикация £-оценок приводит фактически к обобщению определения функции f. В ре­зультате этого обобщения определение функции £ распространяется с узлов на дере­вья. Для дерева, состоящего из отдельного узла (листа), п, было принято такое пер­воначальное определение:

f(и) = g{n) + h(n]

А для дерева Т, корнем которого является узел г., а поддеревьями узла п — дере­вья S , s и т.д., имеет место следующее определение:

f (?) - min f (Si) i

Программа поиска по заданному критерию, разработанная в соответствии с этими соглашениями, приведена в листинге 12.1. Ниже даны некоторые дополнительные пояснения к этой программе.

Основной процедурой программы является процедура expand, которая имеет сле­дующие шесть параметров: expandt ?, Tree, Bound, Treel, Solved, Solution)

Она развертывает текущее дерево (поддерево), при условии, что f-значение этого дерева остается меньшим или равным значению Bound. Ниже приведены определе­ния параметров процедуры expand.

• Р. Путь между начальным узлом и деревом Tree.

• Tree, Текущее дерево (поддерево) поиска.

■ Bound. Текущий f-предел для развертывания дерева Tree.

• Treel. Дерево 3, развернутое л пределах Bound; следовательно, f-значение для Treel больше чем Bound (если только в процессе этого развертывания не най­ден целевой узел).

• Solved. Индикатор, который может принимать значение "yes", "по" или "never".

• Solution, Путь решения от начального узла "через Treel" до целевого узла в пределах Bound (если такой целевой узел существует).