Теоретические сведения. Наряду с понятием случайного события в теории вероятности используется и более удобное понятие случайной величины

Наряду с понятием случайного события в теории вероятности используется и более удобное понятие случайной величины.

Определение:Случайной величиной называется величина, принимающая в результате опыта одно из своих возможных значений, причем заранее неизвестно, какое именно.

Определение:Случайная величина называется дискретной, если она принимает отдельные, изолированные возможные значения с определенными вероятностями.

Определение:Случайная величина называется непрерывной, если множество ее возможных значений целиком заполняет некоторый конечный или бесконечный промежуток.

Определение: Математическим ожиданием (средним значением) дискретной случайной величины называется сумма произведений всех возможных значений этой величины на соответствующие им вероятности и обозначается:

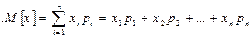
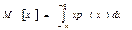- для непрерывной случайной величины

Определение: Дисперсией или рассеяньем дискретной случайной величины называется математическое ожидание квадрата отклонения случайной величины от своего математического ожидания.

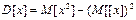
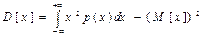- для Непрерывной случайной величины

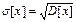- среднее квадратическое отклонение для Дискретной и Непрерывной случайных величин

Пример 1.ВычислитьM[x], D[x], σ[x] по данному закону распределения

х
р	21/252	105/252	105/252	21/252

Решение:

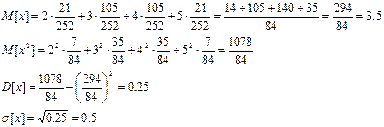
Ответ. M[X]=3.5; D[X]=0.25;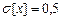

Пример 2. Плотность распределения случайной величины Х имеет вид:

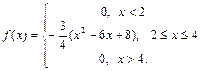
Найти M[x], D[x], σ[x]

Решение.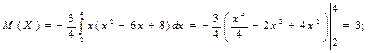

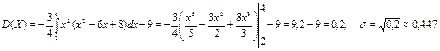
Вывод: Проделав вычисления числовых характеристик ДСВ и НСВ можно сказать, что проводить расчет независимо для какой величины одинаково по сложности. Формулы обладают индивидуальными особенностями относительно каждой случайной величины. Можно сказать, что очевидна их внешняя схожесть и алгоритм вычисления.

Задание для самостоятельной работы:

Подобрать две задачи на вычисление числовых характеристик для дискретной и непрерывной случайных величин. Вычислить математическое ожидание, дисперсию, среднее квадратическое отклонение для ДСВ и НСВ. Сравнить полученные результаты, методы нахождения характеристик и сделать выводы. Оформить согласно требований.

Рекомендуемая литература: 1;2.