Модель одномерного объекта

Объект

Пусть в результате проведения эксперимента получена табличная зависимость значений выходного параметра процесса y от значений входного параметра x:

xy

Рис. 25.1 − Одномерный объект

Требуется получить эмпирическую формулу, описывающую зависимость yотx . Решение такой задачи состоит из двух этапов.

На первом этапе выбирается общий вид формулы, исходя из теоретических представлений о характере изучаемого процесса. Это может быть, например, полином m-степени:

y=a0+a1×x+a2×x²+…+am×x^m.

Формула может содержать тригонометрические, экспоненциальные, логарифмические функции и т.п.

На втором этапе определяются значения параметров a0,a1,a2,…,am эмпирической формулы f(x,a0,a1,a2,…am), которые обеспечивали бы соответствие этой формулы экспериментальным данным.

В соответствии с методом наименьших квадратов параметры a0,a1,a2,…,am выбираются так, чтобы была минимальной сумма квадратов:

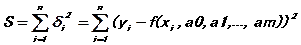(25.1)

Чтобы найти нужные параметры, следует взять частные производные от правой части (25.1) по a0,a1,a2,…,am и приравнять их нулю. Полученную систему уравнений можно решить одним из известных методов.

Пример. Пусть требуется определить параметры a0,a1,a2 формулы

y=a0+a1×x+a2×x²(25.2)

Выражение (25.1) будет тогда иметь вид:

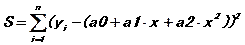
Далее берутся частные производные и приравниваются нулю:

Отсюда

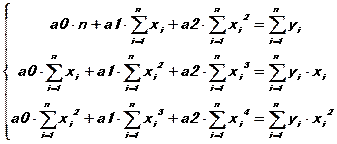(25.3)

Решив систему (25.3) можно определить искомые величины a0, a1, a2.

Алгоритм метода наименьших квадратов для эмпирической формулы (25.2)

1. Ввод количества опытов n, значений x₁, x₂,…x_n, y_1, y₂,…y_n.

2. Определение коэффициентов системы уравнений (21.3):

a_1,2= 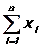, a_1,3= 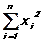, a_2,3= 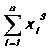, a_3,3= ,

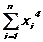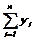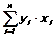b₁= , b₂= , b₃= ;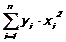

a_1,1=n, a_2,1= a_1,2, a_2,2= a_1,3, a_3,1= a_1,3, a_3,2= a_2,3.

3. Решение системы (25.3) A×Z=B, где A – матрица коэффициентов, B – вектор свободных членов системы, Z – вектор, в котором определяются корни z₁=a0, z₂=a1, z₃=a2.

4. Вывод искомых коэффициентов a0, a1 , a2.

5. Определение и вывод разностей d₁, d₂,…d_n.