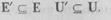Алгебра высказываний (булева алгебра)

Основные понятия

Основное понятие булевой алгебры — выказывание. Под простым высказыванием понимается предложение, о котором можно сказать, истинно оно или ложно (третьего не дано). Высказывания обознача­ются латинскими буквами и могут принимать одно из двух значений: ЛОЖЬ (обозначим 0 ) или ИСТИНА (обозначим 3). Например, со­держание высказывания А: «дважды два равно четырем» истинно А = 1, а высказывание В: «три больше пяти» всегда есть ЛОЖЬ. В дальнейшем нас не будет интересовать содержательная часть выска­зываний, а только их истинность. Два высказывания А и В называ­ются равносильными, если они имеют одинаковые значения истин­ности, записывается А = В.

Логические операции

Сложное высказывание можно построить из простых с помощью логических операций: отрицания, конъюнкции, дизъюнкции, импликации и логических выражений, представляющих собой комбинации логи­ческих операций. Рассмотрим их подробней.

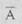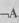Операцией отрицания А называют высказывание (или , го­ворят не А), которое истинно тогда, когда А ложно, и ложно тогда, когда А истинно. Например, если событие А состоит в том, что «зав­тра будет снег», то 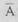«завтра НЕ будет снега», истинность одного утверждения автоматически означает ложность второго. Отрица­ние — унарная (т.е. для одного операнда) логическая операция. Ей соответствует языковая конструкция, использующая частицу НЕ,

Это правило можно записать в виде следующей таблицы:

Такая таблица называется таблицей истинности.

Конъюнкцией (логическим умножением) двух высказываний А и В является новое высказывание С, которое истинно только тогда, ког­да истинны оба высказывания, записывается 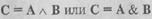(при этом говорят С равно А и В). Примером такой операции может быть следующая: пусть высказывание А состоит в том, что «высота шкафа меньше высоты двери», событие В «ширина шкафа меньше ширины двери», событие С «шкаф можно внести в дверь, если ши­рина шкафа меньше ширины двери И высота шкафа меньше высо­ты двери», т.е. данная операция применяется, если два высказыва­ния связываются союзом И.

Таблица истинности этой операции, как следует из определения, имеет вид

Дизъюнкцией (логическим сложением) двух высказываний А и В является новое высказывание С, которое истинно, если истинно хотя бы одно высказывание. Записывается 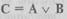(при этом говорят:

С равно А ИЛИ В). Пример такой операции следующий: пусть выс­казывание А состоит в том, что «студент может добираться домой на автобусе», событие В «студент может добираться домой на троллей­бусе», событие С «студент добрался домой на автобусе ИЛИ троллей­бусе», т.е. данная операция применяется, если два высказывания свя­зываются союзом ИЛИ.

Таблица истинности такой операции следующая:

Импликацией двух высказываний А (А называется посылкой) и В (В называется заключением) является новое высказывание С, кото­рое ложно только тогда, когда посылка истинна, а заключение лож­но, записывается 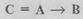(при этом говорят, из А следует В). Примером такой операции может быть любое рассуждение типа: если произошло событие А, то произойдет событие В, «если идет дождь, то на небе тучи». Очевидно, операция не симметрична, т.е. из 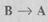не всегда истинно, в нашем примере «если на небе тучи, то идет дождь» не всегда истинно.

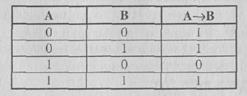
Таблица истинности импликации следующая:

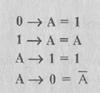
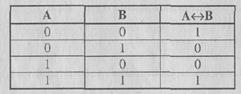
Эквиваленцией двух высказываний А и В является новое выска­зывание С, которое .истинно только тогда, когда оба высказывания имеют одинаковые значения истинности, записывается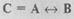

Примером такой операции может быть любое выска­зывание типа: событие А равносильно событию В.

Таблица истинности:

Логические Выражения. Порядок логических операций

С помощью логических операций из простых высказываний (ло­гических переменных и констант) можно построить логические вы­ражения, которые также называются булевскими функциями. Напри­мер.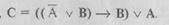

Чтобы избежать большого количества скобок в булевских функ­циях, принято следующее соглашение о старшинстве операций.

Первыми выполняются операции в скобках, затем операции в следующем порядке: отрицание, конъюнкция и дизъюнкция слева направо, импликация, эквиваленция.

Зависимости между логическими операциями

Операции не являются независимыми; одни из них могут быть выражены через другие. Можно доказать с помощью таблиц истин­ности следующие равносильности:

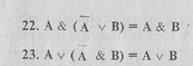
Одну и ту же зависимость между логическими переменными можно выразить различными формулами. Поэтому важно иметь воз­можность приводить формулы с помощью эквивалентных преобра­зований к некоторому стандартному виду. Существует несколько стандартных форм, к которым приводятся логические выражения с помощью эквивалентных преобразований (формул 1—23).

Первая из них - дизъюнктивная нормальная форма (ДНФ), имеет вид 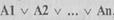, где каждое из составляющих есть конъюнкция простых высказываний и их отрицаний, например:

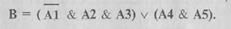
Вторая- конъюнктивная нормальная форма (КНФ), имеет вид

где каждое из составляющих есть дизъюнк­ция простых высказываний и их отрицаний, например:

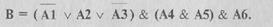
Табличное и алгебраическое задание булевских функций

Задать булевскую функцию можно, определяя ее значения для всех наборов значений аргументов. Каждый аргумент может иметь два значения: 0 и 1, следовательно, n аргументов могут принимать 2ⁿ раз­личных наборов. Пусть, например, булевская функция имеет три ар­гумента: X,, Х₂, Х₃ Общее число наборов 2³ = 8; зададим таблицу ис­тинности функции, указав для каждого набора значение функции.

№	Х1	Х2	Х3	Р
			I

Для составления алгебраической формы по результатам табли­цы сделаем следующее. В комбинациях, где функция принимает зна­чение 1, единицу заменим именем функции, а нуль — именем с от­рицанием (т.е. комбинации 0 0 1 поставим в соответствие выражение 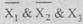), все элементы соединим знаками дизъюнкции, для рассматриваемого примера получим

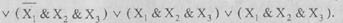
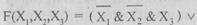
Как нетрудно заметить, построенная функция удовлетворяет за­данной таблице истинности. Функция представляет дизъюнктивную нормальную форму. Кроме того, заметим, что в каждую группу дизъ­юнкций входят все аргументы функции. Такая ДНФ называется со­вершенной, а каждая группа дизъюнкций называется коституентой единицы.

Аналогично, для комбинаций, где функция принимает значение нуля, можно построить алгебраическую форму

,

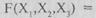
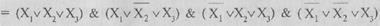кото­рая также удовлетворяет заданной таблице истинности и представ­ляет собой конъюнктивную нормальную форму, в данном случае со­вершенную. Каждая конъюнкция называется конституентой нуля.

В главе 2 будет показано, как, основываясь на булевой алгебре, создаются цифровые устройства.

1.6.2. Элементы теории множеств

Множеством называется любое объединение определенных впол­не различимых объектов; их может и не быть вообще. Можно гово­рить о множестве точек на отрезке [0,1], множестве студентов в груп­пе, множестве снежных дней в июле на экваторе, т.е. множество образуют любые объекты, объединенные по любому признаку. Объек­ты, составляющие множество, называются элементами множества. Множество, не имеющее ни одного элемента, называется пустым, оно обозначается 0. Множество, состоящее из конечного числа эле­ментов, называется конечным, в противном случае — бесконечным.

Задать множество можно перечислением его элементов. Напри­мер, множество образованное из п элементов а_р а₂, ..., а_п, обознача­ется А = {а,, а₂, ..., а_п}; пишется а е А (говорится «элемент а при надлежит множеству А»), если а является элементом множества А, в противном случае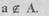

Задать множество можно также, указав общее свойство для всех его и только его элементов. Например, множество точек равноуда­ленных от концов отрезка.

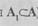Два множества считаются равными, если состоят из одних и тех же элементов; записывается этот факт А = В.

Множество А₁ называется подмножеством А (записываете ),

если все элементы множества А, являются элементами А,

Для множеств определены следующие операции: объединение, пересечение, дополнение.

Объединением множеств А и В (записывается 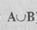) называется

множество, состоящее из элементов как одного, так и второго мно­жества. Например, А и В — множества точек, принадлежащих неко­торым двум кругам, имеющим общие точки, тогда объединением 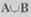будет фигура, состоящая из общих точек.

Пересечением множеств А и В (записывается 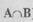) называется

множество, состоящее из элементов, принадлежащих как одному, так и второму множеству одновременно.

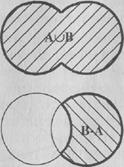Дополнением множества А до В называется множество, состоящее из элементов множества В, не принадлежащих А. Дополнение обо­значается 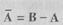(рис. 1.7).

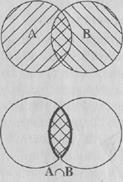
Рис. 1.7. Операции надмножествами

16.3, Элементы теории графов

Основные понятия

Граф задается парой множеств: множества Е, называемого мно­жеством вершин, и множества II, называемого множеством ребер. Ребро 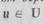есть пара, где ,

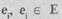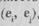
указывающая, между какими двумя вершинами проведено ребро. Говорят, что ребро инцидентно вершинам е., е. Если порядок ребер не имеет значения, т.е. 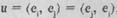, то ребро называется неориентированным или просто ребром, если же порядок имеет значение, то ребро 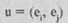называется ориентированным ребром или дугой. Вершина е_i. — назы­вается началом дуги, е_j. - конец дуги. Граф, содержащий хотя бы одну дугу, называется ориентированным графом или орграфом

Граф 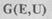называется конечным, если множество Е вершин

конечно.

Граф 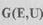•, у которого любые две вершины соединены ребром,

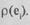называется полным. Если хотя бы две вершины соединены несколь­кими ребрами, то такой граф называется мультиграфом. Две верши­ны 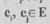называются смежными, если они соединены ребром. Чис­ло ребер, инцидентных данной вершине е., называется локальной степенью этой вершины p(e_i) Число ребер r графа G(Е,U) определя­ется выражением

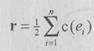, где n — количество вершин в графе. Рассмотрим граф,

изображенный на рис. 1.8.

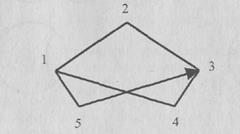
Рис. 1.8. Ориентированный граф

Множество вершин графа состоит из пяти элементов: Е = {1, 2, 3, 4, 5}, а множество ребер U = {(1, 2), (1, 4), (1, 5), (2, 3), (3, 4), {5, 3)}. Ребро (5, 3) - является ориентированным ребром или дугой. Число ребер в графе определяется по значению локальных сте­пеней для каждой вершины:

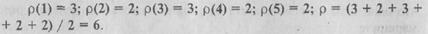
Важным в теории графов является понятие части графа G(Е,U), который обозначается

Множества вершин и ребер части графа являются подмножества­ми вершин и ребер исходного графа