Программирование событий в MATLAB

Изучение основ визуального программирования начнем на простейшем примере программы решения квадратного уравнения .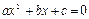

Очевидно, что исходными данными для такой задачи являются вещественные числа 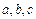. Результатом ее решения станет пара корней уравне-

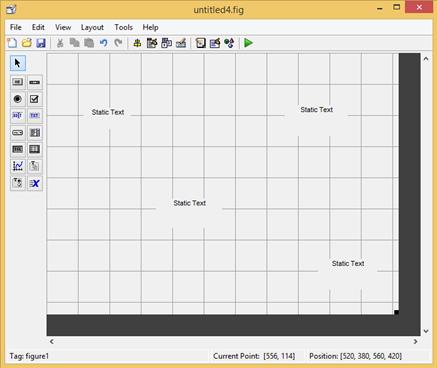
Рис. 2.40.7. Окно с четырьмя компонентами.

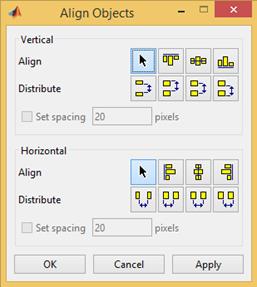
Рис. 2.40.8. Диалоговое окно выравнивания Align Objects.

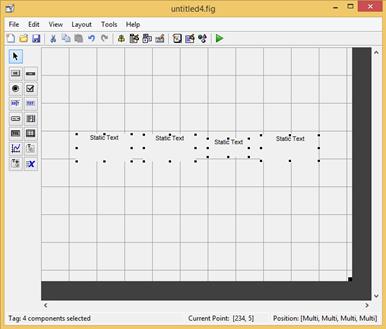
Рис. 2.40.9. Окно с четырьмя компонентами, выравненное по вертикали.

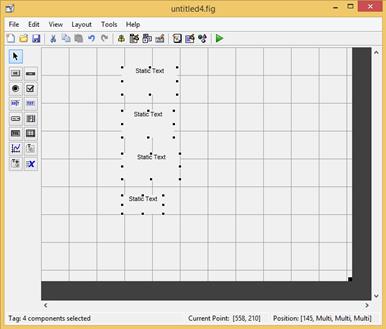
Рис. 2.40.10. Окно с четырьмя компонентами, выравненное по горизонтали.

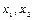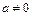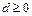ния ( – при , , где 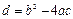– дискриминант), один корень ( 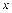– при условии 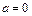) или отсутствие корней (при , ).

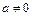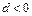Разместим в форме следующие компоненты:

1) Три окна редактирования ( ), которые служат для ввода значений коэффициентов квадратного уравнения ( );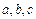

2) Четыре метки ( ), первые три из которых служат для вывода подсказок a=, b=, c= для окон ввода значений переменных 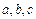соответственно, а четвертая метка будет использоваться для вывода результатов;

3) кнопка, которая будет запускать процесс решения задачи, после того, как пользователь введет значения 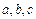в окна редактирования.

В результате окно приложения примет вид, показанный на рис. 2.41.1.

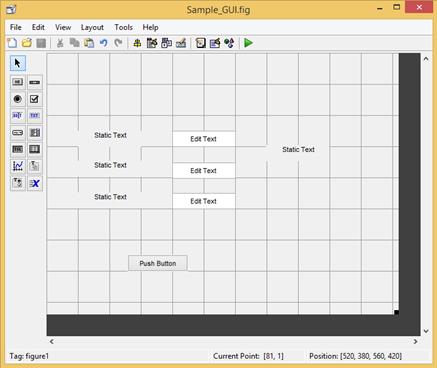
Рис. 2.41.1. Окно приложения после размещения на нем компонентов.

Компоненты являются объектами MATLAB с определенными свойствами. Для изменения этих свойств можно воспользоваться функцией set. Кроме того, с помощью инспектора свойств (Inspector) можно изменить свойства компонентов (объектов), размещенных в форме. После выделения необходимого объекта инспектор свойств можно вызвать либо открыв контекстное меню и выбрав команду Property Inspector, либо на щелкнув на панели инструментов на кнопку . В результате на экране монитора пользователя появится окно инспектора свойств, показанное на рис. 2.41.2.

Рассмотрим основные свойства окна редактирования, метки и кнопки.

Прежде всего отметим, что у всех компонентов одним из основных свойств является Tag – имя компоненты (объекта) в программе (причем сначала компоненты получают имена text1, text2, … (метки); edit1, edit2, … (текстовые поля); pushbutton1, pushbutton2, … (кнопки).

У большинства компонент есть свойство String, определяющее текст для кнопок и меток, а также текст, находящийся в соответствующем текстовом поле. Почти у всех объектов есть свойство Visible, определяющее является ли элемент видимым (значение on) или нет (значение off).

Расположение элемента в форме определяется свойством Position. У графического окна свойства Position – это массив из четырех элементов [xleft,ybottom,width,height], где xleft и ybottom определяют ко-

ординаты левого нижнего угла экрана; width – ширина; height – высота окна (все в пикселях). Для осей параметр Position определяется как массив из четырех элементов [xleft,ybottom,width,height], где величины xleft, ybottom, width и height задаются в относительных координатах графического окна (т.е. ширина и высота окна принимаются равными 1, а левый нижний угол имеет координаты (0,0)).

Расположение элемента в форме определяется свойством Position. У графического окна свойства Position – это массив из четырех элементов [xleft,ybottom,width,height], где xleft и ybottom определяют координаты левого нижнего угла экрана; width – ширина; height – высота окна (все в пикселях). Для осей параметр Position определяется как массив из четырех элементов [xleft,ybottom,width,height], где величины xleft, ybottom, width и height задаются в относительных координатах графического окна (т.е. ширина и высота окна принимаются равными 1, а левый нижний угол имеет координаты (0,0)).

Установим у элементов создаваемого приложения свойства, представленные в таблицах 2.41.1, 2.41.2, после чего форма примет вид, показанный на рис. 2.41.3 (заметим, что цвет фона для первых трех меток был принят желтым (для четвертой – кремовый), размер шрифта установлен 16.0; цвет фона для кнопки принят голубым, размер шрифта установлен 14.0)).

Таблица 2.41.1. Основные свойства объектов задачи (метки).

Свойство	Первая метка	Вторая метка	Третья метка	Четвертая метка
Tag	text_a	text_b	text_c	text_solve
String	a=	b=	c=
Visible	on	On	on	on

Таблица 2.41.2. Основные свойства объектов задачи (текстовые поля, кнопка).

Свойство	Первое текстовое поле	Второе текстовое поле	Третье текстовое поле	Кнопка
Tag	edit_a	edit_b	edit_c	pushbutton_solve
String				Решить уравнение
Visible	on	On	on	on

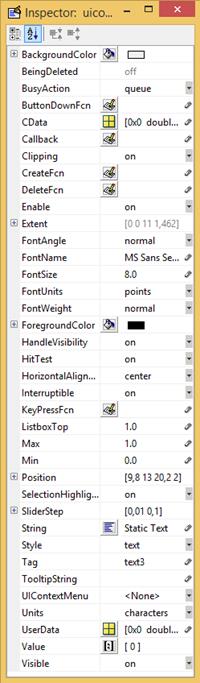
Рис. 2.41.2. Окно инспектора свойств.

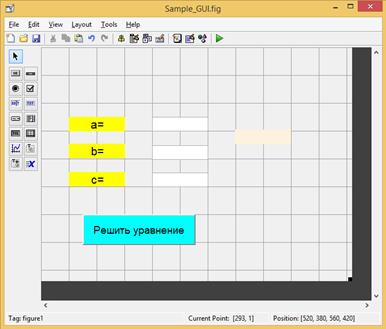
Рис. 2.41.3. Окно приложения после установки свойств компонентов.

Рис. 2.41.4. Общий вид запущенного приложения.

Теперь можно попробовать запустить создаваемое приложение с помощью кнопки или выбрав в главном меню пункт Run и далее в ниспадающем окне указать Run: Sample_GUI (в данном случае Sample_GUI.fig – это имя файла, в котором размещен текст программы – перед запуском, разумеется, следует сохранить приложение (заметим, что после указания имени сохраняемого файла ему автоматически присвоится расширение .fig – в этом файле будет храниться окно приложения; кроме того, будет создан еще один файл с тем же именем, но с расширением .m т.е. Sample_GUI.m – в этом файле будет храниться основная файл-функция для работы с приложением (которая служит для инициализации приложения) и несколько подфункций. После запуска на экран будет выведено окно приложения (рис. 2.41.4), но кнопка Решить уравнение, как и следовало ожидать, не выполнить никаких действий. Для того, чтобы приложение начало работать, требуется написать специальную функцию, реагирующую на щелчок мыши по указанной кнопке, т.е. созданная кнопка должны быть связана с программой обработки событий. Для каждого объекта или совокупности объектов в окне приложения с GUI такая программа, именуемая Callback, создается приложением GUIDE автоматически.

В частности, в файле Sample_GUI.m уже есть пустая подфункция, отвечающая за работу события Callback (так в MATLAB называется «щелчок мыши по компоненту»). Эта функция Pushbutton_Solve_Callback:

% --- Executes on button press in pushbutton_solve.

function pushbutton_solve_Callback(hObject, eventdata, handles)

% hObject handle to pushbutton_solve (see GCBO)

% eventdata reserved - to be defined in a future version of MATLAB

% handles structure with handles and user data (see GUIDATA)

Отметим, что имя функции состоит из имени компонента, символа подчеркивания и имени события (здесь уместно пояснить, что в общем случае функция-обработчик любого события в MATLAB имеет имя вида name_event, где name – имя компонента, а event – имя события, т.е. для того, чтобы построить обработчик любого события, необходимо создать функцию с именем name_event). При написании подфункции следует принять во внимание, что в переменной hObject хранится указатель на объект, событие которого обрабатывается в данный момент (в рассматриваемом случае указанный объект – это кнопка, а переменная handles является структурой с указателями на все объекты (компоненты) приложения. В этой связи для того, чтобы обратиться к любому компоненту следует написать handles.name, где name совпадает со значением свойства Tag соответствующего компонента.

Для доступа ко всем обработчикам кнопки (или какого-либо другого компонента) ее следует выделить, вызвать контекстное меню, в котором выбрать команду ViewCallbacks, и нужный обработчик (Callback).

Таким образом, осталось лишь написать текст функции Pushbutton_Solve_Callback, которая будет выполнять следующие действия:

1) Преобразование считанных строк из текстовых полей text_a, text_b и text_c в вещественные переменные a, b и c.

2) Решение уравнения и формирование по результатам решения строки с корнями (корнем) или сообщения, что корней нет.

3) Отображение результата (строки) в компоненту textSolve.

Текст функции с необходимыми пояснениями в виде комментариев приведен ниже.

% --- Executes on button press in pushbutton_solve.

function pushbutton_solve_Callback(hObject, eventdata, handles)

% hObject handle to pushbutton_solve (see GCBO)

% eventdata reserved - to be defined in a future version of MATLAB

% handles structure with handles and user data (see GUIDATA)

% Считываем из компоненты edit_a строку,

% которую преобразовываем в вещественное число a

% (для получения строки считывается свойство String

% из компонента с именем edit_a с помощью функции get,

% обращение к нетекущему компоненту осуществляется

% с помощью функции handles.edit_a

a=str2double(get(handles.edit_a,'String'));

% Считываем из компонента с именем edit_b строку,

% которую преобразовываем в вещественное число b

b=str2double(get(handles.edit_b,'String'));

% Считываем из компонента с именем edit_c строку,

% которую преобразовываем в вещественное число c

c=str2double(get(handles.edit_c,'String'));

if a==0

% Квадраное уравнение сводится к линейному

x=-c/b;

% Формирование строки с результатом

S=sprintf('X=%g\t',x);

else

d=b*b-4*a*c

if d<0

% Случай отрицательного дискриминанта

% Формирование строки с результатом

S='Действительных корней нет';

else

% Случай неотрицательного дискриминанта

x1=(-b+sqrt(d))/(2*a);

x2=(-b-sqrt(d))/(2*a);

% Формирование строки с результатом

S=sprintf('X1=%g\t X2=%g',x1,x2);

end

end

% Свойство компонента handles.textSolve String

% равно S, что приводит к выводу текста S

% на метку handles.textSolve

set(handles.textSolve,'String',S);

Запустив теперь рассматриваемое приложение на выполнение, введя значения коэффициентов a, b и c, после щелчка по кнопке Решить уравнение, получим ожидаемо верные результате, представленные на рис. 2.41.5.

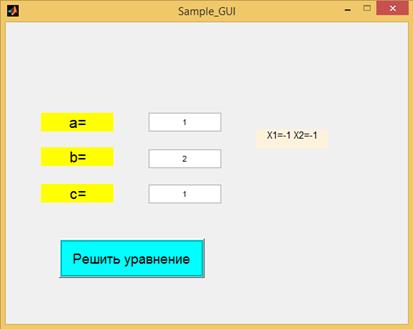
Рис. 2.41.5. Окно приложения решения квадратного уравнения.

Итак, было создано законченное графическое приложение, решающее проблему отыскания корней квадратного уравнения, при этом можно выделить следующие основные этапы разработки: размещение компонентов в окне приложения, установка основных свойств компонентов, написание функций-обработчиков событий.