Организационные проблемы криптозащиты
Рассмотренные значения стойкости шифров являются потенциальными величинами. Они могут быть реализованы при строгом соблюдении правил использования криптографических средств защиты.
Основные правила криптозащиты:
1. Сохранение в тайне ключей.
2. Исключение дублирования.
3. Достаточно частая смена ключей.
Под дублированием здесь понимается повторное шифрование одного и того же отрывка текста с использованием тех же ключей (например, если при первом шифровании произошел сбой). Нарушение этого правила резко снижает надежность шифрования, так как исходный текст может быть восстановлен с помощью статистического анализа двух вариантов зашифрованного текста.
Важнейшим правилом криптозащиты является достаточно частая смена ключей. Причем частота может определяться исходя из длительности использования ключа или исходя из объема зашифрованного текста. При этом смена ключей по временному графику является защитной мерой против возможного их хищения, смена после шифрования определенного объема текста - от раскрытия шифра статистическими методами.
Нельзя допускать злоумышленнику возможности направить в систему ряд специально подобранных сообщений и получать их в зашифрованном виде. Такого взлома не может выдержать ни одна криптосистема!
Важными аспектами организации криптозащиты являются выбор способа закрытия, распределение ключей и доставка их в места пользования (механизм распределения ключей).
Выбор способа защиты тесно связан с трудоемкостью метода шифрования, степенью секретности закрываемых данных, стойкостью метода и объемом шифруемой информации.
Один из принципов криптографии является предположение о несекретности метода закрытия информации. Предполагается, что необходимая надежность закрытия обеспечивается только за счет сохранения в тайне ключей. Отсюда вытекает принципиальная важность формирования ключей, распределения их и доставка в пункты назначения. Основными правилами механизма распределения ключей являются:
1. Ключи должны выбираться случайно.
2. Выбранные ключи должны распределяться таким образом, чтобы не было закономерностей в изменении ключей от пользователя к пользователю.
3. Должна быть обеспечена тайна ключей на всех этапах функционирования системы. Ключи должны передаваться по линиям связи, почте или курьерами в зашифрованном виде с помощью другого ключа. На практике часто образуется иерархия ключей шифрования, в которой ключи нижнего уровня при пересылке шифруются с помощью ключей верхнего уровня. Ключ в вершине иерархии не шифруется, а задается и хранится у доверенного лица, рассылается пользователям курьерами. Чем ниже уровень ключа, тем чаще он меняется и рассылается по линиям связи. Подобная схема шифрования ключей часто используется в сетях.
Литература
1. Герасименко В.А., Размахнин М.К. "Криптографические методы в автоматизированных системах" Зарубежная радиоэлектроника,1982,N8
2. Сяо Д., Керр Д., С.Мэдник "Защита ЭВМ",М.,Мир,1982 - рассмотрены практически все аспекты защиты информации в вычислительных и автоматизированных системах.
3. Хоффман Л.Дж. Современные методы защиты информации. М.,Сов.радио, 1980 - наиболее полная и серьезная монография по теории и практике защиты информации
4. Джефф П.Р. Электроника,1973,т.46,N1 - шифрование данных методом гаммирования.
5. Уолкер Б.Дж., Блейк Я.Ф. Безопасность ЭВМ и организация их защиты.-М.:Связь,1980 - рассматриваются криптографические методы защиты информации, защита данных в файлах или базах данных.
6. Мануильямс Ф.Ж.,Слоан Н.Дж. ТИИЭР,1976,т.64,N12 - детально описаны способы формирования и свойства псевдослучайных последовательностей, которые используются при шифровании данных методом гаммирования.
Стандарт шифрования данных
Data Encryption Standard
В 1977 году Национальное бюро Стандартов США (NBS) опубликовало стандарт шифрования данных Data Encryption Standard (DES), предназначенный для использования в государственных и правительственных учреждениях США для защиты от несанкционированного доступа важной, но несекретной информации. Алгоритм, положенный в основу стандарта, распространялся достаточно быстро, и уже в 1980 году был одобрен ANSI. С этого момента DES превращается в стандарт не только по названию (Data Encryption Standard), но и фактически. Появляются программное обеспечение и специализированные микроЭВМ, предназначенные для шифрования/расшифрования информации в сетях передачи данных и на магнитных носителях. К настоящему времени DES является наиболее распространенным алгоритмом, используемым в системах защиты коммерческой информации. Более того реализация алгоритма DES в таких системах является просто признаком хорошего тона! За примерами далеко ходить не надо. Программа DISKREET из пакета Norton Utilities, предназначенная для создания зашифрованных разделов на диске, использует именно алгоритм DES. "Собственный алгоритм шифрования" отличается от DES только числом итераций при шифровании. Почему же DES добился такой популярности?
Основные достоинства алгоритма DES:
- используется только один ключ длиной 56 битов;
- зашифровав сообщение с помощью одного пакета, для расшифровки вы можете использовать любой другой;
- относительная простота алгоритма обеспечивает высокую скорость обработки информации;
- достаточно высокая стойкость алгоритма.
DES осуществляет шифрование 64-битовых блоков данных с помощью 56-битового ключа. Расшифрование в DES является операцией обратной шифрованию и выполняется путем повторения операций шифрования в обратной последовательности (несмотря на кажущуюся очевидность, так делается далеко не всегда. Позже мы рассмотрим шифры, в которых шифрование и расшифрование осуществляются по разным алгоритмам).
Процесс шифрования заключается в начальной перестановке битов 64-битового блока, шестнадцати циклах шифрования и, наконец, обратной перестановки битов (рис.1).
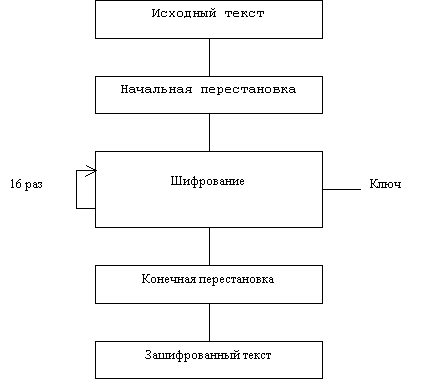
Рис.1. Обобщенная схема шифрования в алгоритме DES
Необходимо сразу же отметить, что ВСЕ таблицы, приведенные в данной статье, являются СТАНДАРТНЫМИ, а следовательно должны включаться в вашу реализацию алгоритма в неизменном виде. Все перестановки и коды в таблицах подобраны разработчиками таким образом, чтобы максимально затруднить процесс расшифровки путем подбора ключа. Структура алгоритма DES приведена на рис.2.
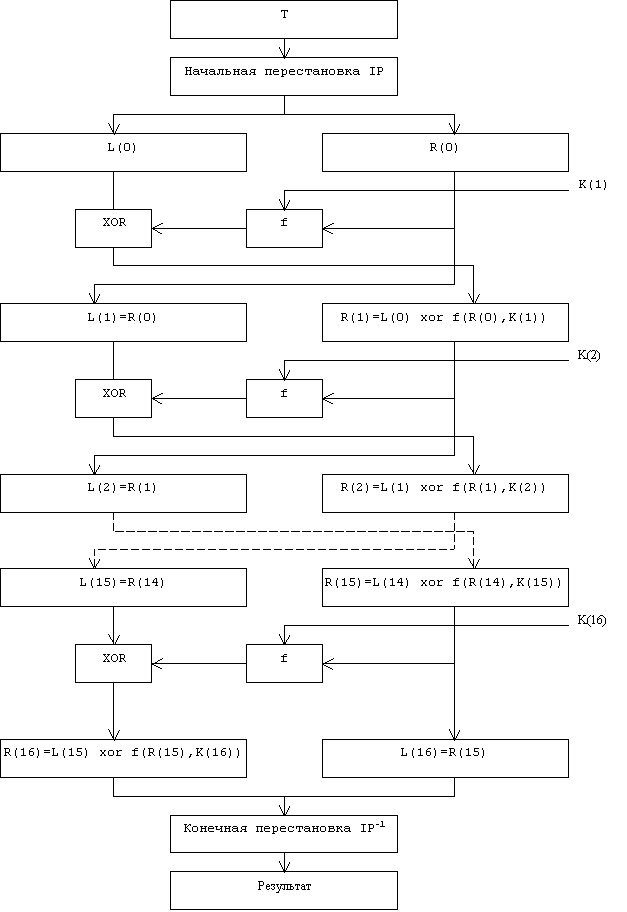
Рис.2. Структура алгоритма шифрования DES
Пусть из файла считан очередной 8-байтовый блок T, который преобразуется с помощью матрицы начальной перестановки IP (табл.1) следующим образом: бит 58 блока T становится битом 1, бит 50 - битом 2 и т.д., что даст в результате: T(0) = IP(T).
Полученная последовательность битов T(0) разделяется на две последовательности по 32 бита каждая: L(0) - левые или старшие биты, R(0) - правые или младшие биты.
Таблица 1: Матрица начальной перестановки IP
58 50 42 34 26 18 10 0260 52 44 36 28 20 12 0462 54 46 38 30 22 14 0664 56 48 40 32 24 16 0857 49 41 33 25 17 09 0159 51 43 35 27 19 11 0361 53 45 37 29 21 13 0563 55 47 39 31 23 15 07Затем выполняется шифрование, состоящее из 16 итераций. Результат i-й итерации описывается следующими формулами:
| L(i) = R(i-1) R(i) = L(i-1) xor f(R(i-1), K(i)) , |
где xor - операция ИСКЛЮЧАЮЩЕЕ ИЛИ.
Функция f называется функцией шифрования. Ее аргументы - это 32-битовая последовательность R(i-1), полученная на (i-1)-ой итерации, и 48-битовый ключ K(i), который является результатом преобразования 64-битового ключа K. Подробно функция шифрования и алгоритм получения ключей К(i) описаны ниже.
На 16-й итерации получают последовательности R(16) и L(16) (без перестановки), которые конкатенируют в 64-битовую последовательность R(16)L(16).
Затем позиции битов этой последовательности переставляют в соответствии с матрицей IP-1 (табл.2).
Таблица 2: Матрица обратной перестановки IP-1
40 08 48 16 56 24 64 3239 07 47 15 55 23 63 3138 06 46 14 54 22 62 3037 05 45 13 53 21 61 2936 04 44 12 52 20 60 2835 03 43 11 51 19 59 2734 02 42 10 50 18 58 2633 01 41 09 49 17 57 25Матрицы IP-1 и IP соотносятся следующим образом: значение 1-го элемента матрицы IP-1 равно 40, а значение 40-го элемента матрицы IP равно 1, значение 2-го элемента матрицы IP-1 равно 8, а значение 8-го элемента матрицы IP равно 2 и т.д.
Процесс расшифрования данных является инверсным по отношению к процессу шифрования. Все действия должны быть выполнены в обратном порядке. Это означает, что расшифровываемые данные сначала переставляются в соответствии с матрицей IP-1, а затем над последовательностью бит R(16)L(16) выполняются те же действия, что и в процессе шифрования, но в обратном порядке.
Итеративный процесс расшифрования может быть описан следующими формулами:
| R(i-1) = L(i), i = 1, 2, ..., 16; L(i-1) = R(i) xor f(L(i), K(i)), i = 1, 2, ..., 16 . |
На 16-й итерации получают последовательности L(0) и R(0), которые конкатенируют в 64-битовую последовательность L(0)R(0).
Затем позиции битов этой последовательности переставляют в соответствии с матрицей IP. Результат такой перестановки - исходная 64-битовая последовательность.
Теперь рассмотрим функцию шифрования f(R(i-1),K(i)). Схематически она показана на рис. 3.
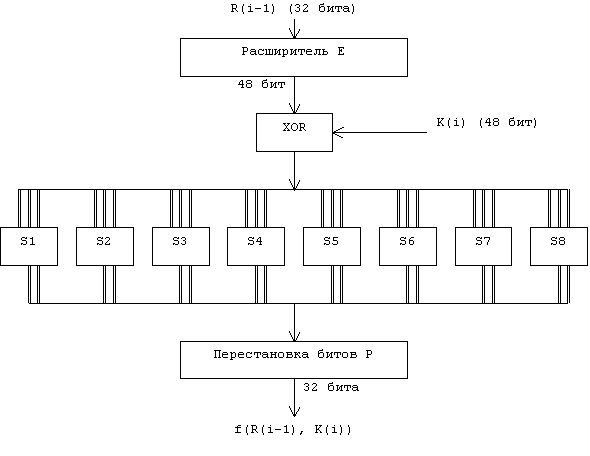
Рис.3. Вычисление функции f(R(i-1), K(i))
Для вычисления значения функции f используются следующие функции-матрицы:
- Е - расширение 32-битовой последовательности до 48-битовой,
- S1, S2, ... , S8 - преобразование 6-битового блока в 4-битовый,
- Р - перестановка бит в 32-битовой последовательности.
Функция расширения Е определяется табл.3. В соответствии с этой таблицей первые 3 бита Е(R(i-1)) - это биты 32, 1 и 2, а последние - 31, 32 и 1.
Таблица 3:Функция расширения E
32 01 02 03 04 0504 05 06 07 08 0908 09 10 11 12 1312 13 14 15 16 1716 17 18 19 20 2120 21 22 23 24 2524 25 26 27 28 2928 29 30 31 32 01Результат функции Е(R(i-1)) есть 48-битовая последовательность, которая складывается по модулю 2 (операция xor) с 48-битовым ключом К(i). Получается 48-битовая последовательность, которая разбивается на восемь 6-битовых блоков B(1)B(2)B(3)B(4)B(5)B(6)B(7)B(8). То есть:
E(R(i-1)) xor K(i) = B(1)B(2)...B(8) .
Функции S1, S2, ... , S8 определяются табл.4.
| Таблица 4 Функции преобразования S1, S2, ..., S8 | ||||||||||||||||||||||||||||
|
К табл.4. требуются дополнительные пояснения. Пусть на вход функции-матрицы Sj поступает 6-битовый блок B(j) = b1b2b3b4b5b6, тогда двухбитовое число b1b6 указывает номер строки матрицы, а b2b3b4b5 - номер столбца. Результатом Sj(B(j)) будет 4-битовый элемент, расположенный на пересечении указанных строки и столбца.
Например, В(1)=011011. Тогда S1(В(1)) расположен на пересечении строки 1 и столбца 13. В столбце 13 строки 1 задано значение 5. Значит, S1(011011)=0101.
Применив операцию выбора к каждому из 6-битовых блоков B(1), B(2), ..., B(8), получаем 32-битовую последовательность S1(B(1))S2(B(2))S3(B(3))...S8(B(8)).
Наконец, для получения результата функции шифрования надо переставить биты этой последовательности. Для этого применяется функция перестановки P (табл.5). Во входной последовательности биты перестанавливаются так, чтобы бит 16 стал битом 1, а бит 7 - битом 2 и т.д.
Таблица 5:Функция перестановки P
16 07 20 2129 12 28 1701 15 23 2605 18 31 1002 08 24 1432 27 03 0919 13 30 0622 11 04 25Таким образом,
f(R(i-1), K(i)) = P(S1(B(1)),...S8(B(8)))
Чтобы завершить описание алгоритма шифрования данных, осталось привести алгоритм получения 48-битовых ключей К(i), i=1...16. На каждой итерации используется новое значение ключа K(i), которое вычисляется из начального ключа K. K представляет собой 64-битовый блок с восемью битами контроля по четности, расположенными в позициях 8,16,24,32,40,48,56,64.
Для удаления контрольных битов и перестановки остальных используется функция G первоначальной подготовки ключа (табл.6).
Таблица 6
Матрица G первоначальной подготовки ключа
Результат преобразования G(K) разбивается на два 28-битовых блока C(0) и D(0), причем C(0) будет состоять из битов 57, 49, ..., 44, 36 ключа K, а D(0) будет состоять из битов 63, 55, ..., 12, 4 ключа K. После определения C(0) и D(0) рекурсивно определяются C(i) и D(i), i=1...16. Для этого применяют циклический сдвиг влево на один или два бита в зависимости от номера итерации, как показано в табл.7.
| Таблица 7 Таблица сдвигов для вычисления ключа | ||||
|
Полученное значение вновь "перемешивается" в соответствии с матрицей H (табл.8).
Таблица 8:Матрица H завершающей обработки ключа
14 17 11 24 01 0503 28 15 06 21 1023 19 12 04 26 0816 07 27 20 13 0241 52 31 37 47 5530 40 51 45 33 4844 49 39 56 34 5346 42 50 36 29 32Ключ K(i) будет состоять из битов 14, 17, ..., 29, 32 последовательности C(i)D(i). Таким образом:
K(i) = H(C(i)D(i))
Блок-схема алгоритма вычисления ключа приведена на рис.4.
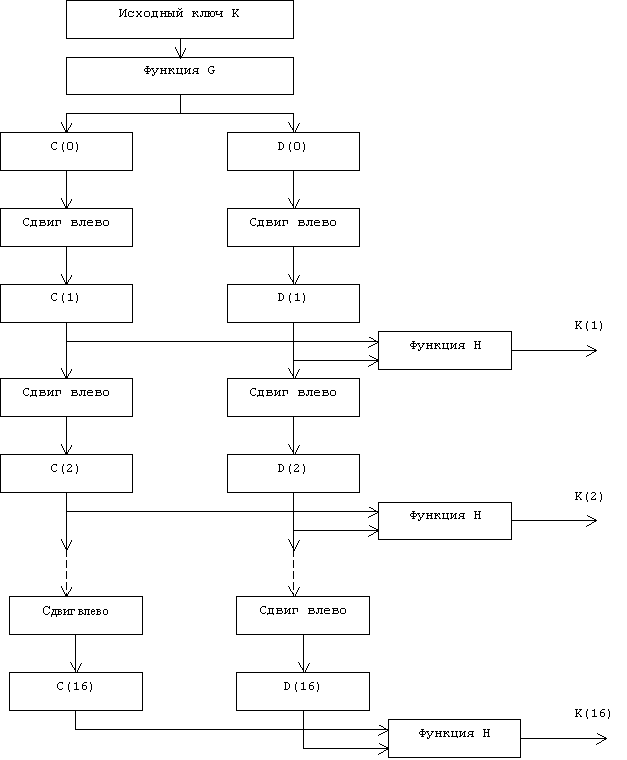
Рис.4. Блок-схема алгоритма вычисления ключа K(i)
Восстановление исходного текста осуществляется по этому алгоритму, но вначале вы используете ключ
K(15), затем - K(14) и так далее. Теперь вам должно быть понятно, почему автор настойчиво рекомендует использовать приведенные матрицы. Если вы начнете самовольничать, вы, должно быть, получите очень секретный шифр, но вы сами не сможете его потом раскрыть!
