Распространение числовой волны

ЛАБОРАТОРНАЯ РАБОТА № 7

ИССЛЕДОВАНИЕ ЭФФЕКТИВНОСТИ АЛГОРИТМОВ

ТРАССИРОВКИ ПЕЧАТНЫХ И ПЛЕНОЧНЫХ СОЕДИНЕНИЙ

Цель работы – исследовать эффективность алгоритмов трассировки печатных и пленочных соединений; освоить особенности алгоритмизации и программирования задач трассировки печатных соединений на современных ЭВМ волновыми и лучевым алгоритмами; приобрести навык построения математических моделей объектов конструирования, реализации и иссле-дования их при решении задачи трассировки в САПР.

СВЕДЕНИЯ ИЗ ТЕОРИИ

Многие методы трассировки печатных соединений основаны на идеях волнового алгоритма, предложенного С. Ли [1 – 4]. Он представляет собой развитие алгоритмов построения кратчайших путей в сети и позволяет на-ходить маршруты соединений, оптимальные по ряду параметров. Данный алгоритм является классическим примером использования методов динами-ческого программирования.

Волновой алгоритм C. Ли

Монтажное поле разбивается на элементарные ячейки. Размеры ячеек и их количество определяются площадью поля, допустимой плотностью располо-жения выводов элементов и проводников. В простейшем случае ячейка пред-ставляет собой квадрат со стороной h, равной расстоянию между средними линиями двух соседних печатных проводников (рис.7.1).

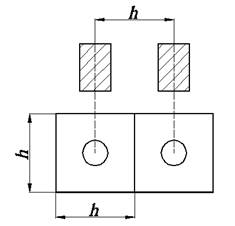
Рис. 7.1.

Если размеры поля по горизонтали и вертикали соответственно A_x и B_y, то получим дискретное рабочее поле (ДРП) с N_x ´ N_y ячейками:

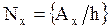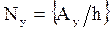, , (7.1)

где 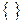– символ ближайшего большего целого.

В данном ДРП (рис.7.2) определяется множество занятых ячеек, соответ-ствующее зонам, запрещенным для проведения соединений: выводы элементов, технологические области, ранее проведенные соединения и т. д. По мере прове-дения соединений множества занятых и свободных ячеек изменяются.

Основу всех модификаций волнового алгоритма С. Ли составляет процеду-ра построения оптимального в заданном смысле пути между двумя известными ячейками ДРП. Процедура состоит из двух этапов: поиска пути и проведения пути.

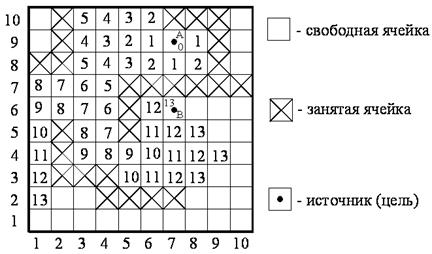
Рис.7.2.

На первом этапе из одной из заданных ячеек ДРП – источника моделиру-ется распространение числовой волны до тех пор, пока ее фронт не достиг второй отмеченной ячейки ДРП – цели, либо наступает момент, когда в оче-редной фронт нельзя включить ни одну новую не занятую ячейку ДРП.

В первом случае искомый путь существует, во втором – нет.

Все условия, которые необходимо выполнить при проведении соединения, в том числе и условия оптимальности, должны быть заложены в правила движе-ния волны, т. е. в правила построения очередного фронта волны. В процессе распространения волны ячейкам ДРП присваиваются весовые оценки, связанные с принятым критерием оптимальности.

На втором этапе алгоритма осуществляется проведение пути. Для этого следует, начиная от ячейки-цели, двигаться в направлении, противоположном направлению волны, переходя последовательно от ячейки с большим весом к соседней ячейке с меньшим весом до тех пор, пока не будет достигнута ячейка-источник. Ячейки ДРП, выделенные в ходе указанного процесса, и определяют искомое оптимальное соединение.

Распространение числовой волны

Образование очередного фронта волны 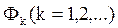начинается с присво-ения всем свободным, ранее не помеченным ячейкам, соседним с ячейками предыдущего фронта 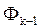, веса .

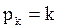Соседними с данной ячейкой 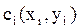могут быть ячейки двух видов:

1) Ячейки ДРП, которые имеют с ней общее ребро (рис.7.3):

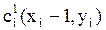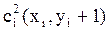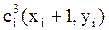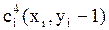; ; ; . Очередной фронт волны распространяется по четырем направлениям.

	xi(yi+1)
(xi-1)yi	xiyi	(xi+1)yi
	xi(yi-1)

Рис.7.3.

2) Ячейки ДРП, которые имеют с ней хотя бы одну общую точку (рис.7.4) 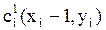; ; 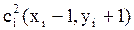; ; 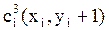; ; 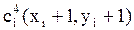; 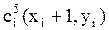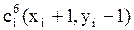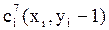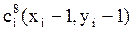. Очередной фронт волны распространяется в свободные ячейки по восьми направлениям.

(xi-1) (yi+1)	xi(yi+1)	(xi+1) (yi+1)
(xi-1)yi	xiyi	(xi+1)yi
(xi-1) (yi-1)	xi(yi-1)	(xi+1) (yi-1)

Рис. 7.4

Рассмотрим вначале 1-й случай.

Результат распространения волны от источника A представлен на рис.7.2. Между ячейками A и B существует путь длиной 13. Трасса пути показана на рис.7.5. В этом случае трассы прокладываются только под углами в 90^о.

Для сокращения числа поворотов пути на этапе проведения может быть принято следующее правило приоритета. При переходе от ячейки фронта 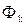к ячейке фронта 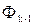следует, по возможности, сохранять направление, опреде-ляемое переходом от ячейки 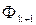к ячейке .

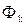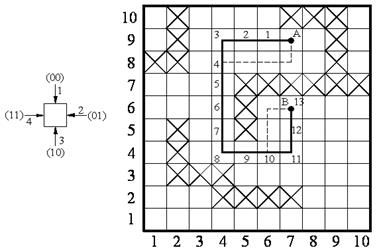
Рис.7.5.

В данном случае вес, присваиваемый ячейке фронта 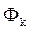, равен расстоянию этой ячейки от источника в ортогональной метрике.

Во втором случае результат распространения волны от того же источника A представлен на рис.7.6. Но здесь длина пути между ячейками AиB равна 8. Трасса пути показана на рис.7.7. Видим, что во втором случае трассы могут проводиться под любыми углами.

Чтобы исключить неопределенность при проведении пути для случая, когда несколько ячеек имеют одинаковый минимальный вес, вводят понятие путевых координат, задающих предпочтительность проведения трассы. Каждое направление кодируют двоичным числом по 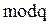, где q – число просматриваемых соседних ячеек. При этом чем более предпочтительно то или иное направление, тем меньший числовой код оно имеет. Например, если задаться приоритетным порядком проведения пути сверху, справа, снизу и слева, то коды соответствующих путевых координат будут 00, 01, 10 и 11. Присвоение путевых координат производят на этапе распространения волны. При проведении пути движение от ячейки к ячейке осуществляют по путевым координатам.

В первом случае (рис.7.5) приоритетный порядок проведения пути задан: сверху, справа, снизу и слева. Во втором случае (рис.7.7) – сверху, с правого верхнего угла, справа, с правого нижнего угла, снизу, с левого нижнего угла, слева и с левого верхнего угла.

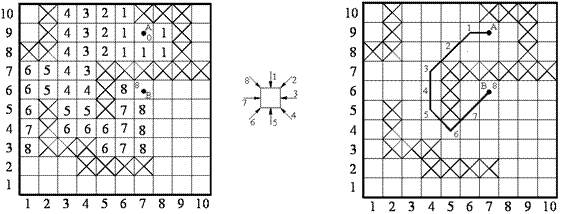
Рис.7.6. Рис.7.7.