Грамматики с ограничениями на правила

ЛЕКЦИЯ № 3 ТЕОРИЯ ЯЗЫКОВ И ФОРМАЛЬНЫХ ГРАММАТИК

Способы определения языков

Описание языков программирования во многом опирается на теорию формальных языков. Эта теория является фундаментом для организации синтаксического анализа и перевода.

Существует два основных способа определения языков:

– механизм порождения или генератор;

– механизм распознавания или распознаватель.

Они тесно связаны. Первый обычно используется для описания языков, а второй для их реализации. Оба способа позволяют описать языки конечным образом, несмотря на бесконечное число порождаемых ими цепочек.

Неформально язык L - это множество цепочек конечной длины в алфавите T. Механизм порождения позволяет описать языки с помощью системы правил, называемой грамматикой. Цепочки (предложения) языка строятся в соответствии с этими правилами. Достоинство определения языка с помощью грамматик в том, что операции, производимые в ходе синтаксического анализа и перевода, можно делать проще, если воспользоваться структурой, предписываемой цепочкам с помощью этих грамматик.

Механизм распознавания использует алгоритм, который для произвольной входной цепочки остановится и ответит «да» после конечного числа шагов, если эта цепочка принадлежит языку. Если цепочка не принадлежит языку, алгоритм ответит «нет». Распознаватели используются непосредственно при построении синтаксических анализаторов и являются как бы их формальной моделью. Распознаватели строятся на основе теорий конечных автоматов и автоматов с магазинной памятью.

Формальные грамматики

Грамматикой называется четверка

G = (N, T, P, S), (3.1)

где N - конечное множество нетерминальных символов

(нетерминалов),

T - множество терминалов (не пересекающихся с N),

S - символ из N, называемый начальным,

Р - конечное подмножество множества, называемого множеством правил: .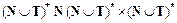

Множество правил Р описывает процесс порождения цепочек языка. Элемент p_i = (a, b) множества Р называется правилом (продукцией) и записывается в виде a Þ b. Здесь aи b - цепочки, состоящие из терминалов и нетерминалов. Данная запись может читаться одним из следующих способов:

– цепочка a порождает цепочку b;

– из цепочки a выводится цепочка b.

Таким образом, правило P имеет две части: левую, определяемую, и правую, подставляемую. То есть правило p_i - это двойка (p_i1, p_i2), где p _i1 = 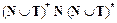- цепочка, содержащая хотя бы один нетерминал, p_i2 = 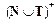произвольная, возможно пустая цепочка (e - цепочка).

Если цепочка a содержит p_i1, то, в соответствии с правилом p_i, можно образовать новую цепочку b, заменив одно вхождение p_i1 на p_i2. Говорят также, что цепочка b выводится из a в данной грамматике.

Для описания абстрактных языков в определениях и примерах используются следующие обозначения:

– терминалы обозначаются буквами a,b,c,d или цифрами 0,1, ...,9;

– нетерминалы обозначаются буквами A, B, C, D, S (причем нетерминал S - начальный символ грамматики);

– буквы U, V, ..., Z используются для обозначения отдельных терминалов или нетерминалов;

– через a, b, g ... обозначаются цепочки терминалов и нетерминалов;

– u, v, w, x, y, z - цепочки терминалов;

– для обозначения пустой цепочки (не содержащей ни одного символа) используется знак e;

– знак «®» отделяет левую часть правила от правой и читается как «порождает» или «есть по определению». Например, A ®cd, читается как «A порождает cd».

Эти обозначения определяют некоторый язык, предназначенный для описания правил построения цепочек, а значит, для описания других языков. Язык, предназначенный для описания другого языка, называется метаязыком.

Пример грамматики G1:

G1 = ({A, S}, {0, 1}, P, S), (3.2)

где P:

1. S ® 0A1;

2. 0A ® 00A1;

3. A ® e.

Выводимая цепочка грамматики G, не содержащая нетерминалов, называется терминальной цепочкой, порождаемой грамматикой G.

Язык L(G), порождаемый грамматикой G, - это множество терминальных цепочек, порождаемых грамматикой G.

Введем отношение Þ_G непосредственного вывода на множестве 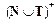, которое записывается следующим образом:

j Þ_G y(3.3)

Данная запись читается: y непосредственно выводима из j для грамматики G = (N, T, P, S) и означает: если abg – цепочка из множества 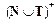и b ® d – правило из Р, то abg Þ_G adg.

Через Þ_G⁺ обозначим транзитивное замыкание (нетривиальный вывод за один и более шагов). Тогда j Þ_G⁺ y читается как: y выводима из j нетривиальным образом.

Через Þ_G^* обозначим рефлексивное и транзитивное замыкание (вывод за ноль и более шагов). Тогда j Þ_G^* y означает: y выводима из j.

Пусть Þ^K – k-я степень отношения Þ. То есть, если a Þ^K b, то существует последовательность a₀ a₁ a₂ a₃ ... a_k из к+1 цепочек

a = a₀, a₁, ... a_{i - 1} Þ a_i, 1 ≤ i ≤ k и a_k = b (3.4)

Пример выводов для грамматики G1:

S Þ 0A1 Þ 00A11 Þ 0011; (3.5)

S Þ¹ 0A1; S Þ² 00A11; S Þ³ 0011; (3.6)

S Þ⁺ 0A1; S Þ⁺ 00A11; S Þ⁺ 0011; (3.7)

S Þ* S; S Þ* 0A1; S Þ* 00A11; S Þ* 0011, (3.8)

где 0011 Ì L(G1).

Грамматики с ограничениями на правила

Несмотря на большое разнообразие грамматик, при построении трансляторов нашли широкое применение только ряд из них, имеющих некоторые ограничения. Это связано с практической целесообразностью использования определенных типов правил, так как сложность их построения непосредственно влияет на сложность построения трансляторов. По виду правил выделяют несколько классов грамматик. В соответствии с классификацией Хомского грамматика G называется:

– праволинейной, если каждое правило из Р имеет вид:

A ® xB или A ® x, (3.9)

где A, B - нетерминалы,

x - цепочка, состоящая из терминалов;

– контекстно-свободной(КС) или бесконтекстной, если каждое правило из Р имеет вид: A® a, где A Î N, а a Î 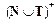, то есть является цепочкой, состоящей из множества терминалов и нетерминалов, возможно пустой;

– контекстно-зависимой (КЗ) или неукорачивающей, если каждое правило из P имеет вид: a ® b, где |a| £ |b|. То есть, вновь порождаемые цепочки не могут быть короче, чем исходные, а, значит, и пустыми (другие ограничения отсутствуют);

– грамматикой свободного вида, если в ней отсутствуют выше упомянутые ограничения.

Пример праволинейной грамматики:

G2 = ({S,}, {0,1}, P, S), (3.10)

где P:

1. S ® 0S;

2. S ® 1S;

3. S ® e,

определяет язык {0, 1}*.

Пример КС-грамматики:

G3 = ({E, T, F}, {a, +, *, (,)}, P, E), (3.11)

где P:

1. E ®T;

2. E ® E + T;

3. T ® F;

4. T ® T * F;

5. F ® (E);

6. F ® a.

Данная грамматика порождает простейшие арифметические выражения.

Пример КЗ-грамматики:

G4 = ({B, C, S}, {a, b, c}, P, S), (3.12)

где P:

1. S ® aSBC;

2. S ® abc;

3. CB ® BC;

4. bB ® bb;

5. bC ® bc;

6. cC ® сc,

порождает язык { aⁿ bⁿ cⁿ }, n ≥ 1.

Примечание 1. Согласно определению каждая праволинейная грамматика является контекстно-свободной.

Примечание 2. По определению КЗ-грамматика не допускает правил: А ® e, где e - пустая цепочка. Т.е. КС-грамматика с пустыми цепочками в правой части правил не является контекстно-зависимой. Наличие пустых цепочек ведет к грамматике без ограничений.

Соглашение. Если язык L порождается грамматикой типа G, то L называется языком типа G.

Пример: L(G3) - КС язык типа G3.

Наиболее широкое применение при разработке трансляторов нашли КС-грамматики и порождаемые ими КС-языки. В дальнейшем при изучении КС-языков будут рассматриваться только полезные для нас с практической точки зрения (теория языков весьма обширна и для детального ее изучения необходимо много времени). Для получения углубленных знаний рекомендуется обратиться к фундаментальной монографии Ахо и Ульмана [14].