В19. Модели, описываемые обыкновенными дифференциальными уравнениями. Классификация, методы решения. Методы Рунге-Кутта и прогноза и коррекции.

Любое дифференциальное уравнение или система дифференциальных уравнений описывает с определенной степенью точности реальный физический процесс. Приборы, фиксирующие то или иное физическое явление, не совершенны. Может оказаться, что малая погрешность измерения начальных данных вызывает ”ощутимые” изменения решений уравнений. В этой ситуации нельзя гарантировать, что выбранная математическая модель реально отражает описываемое ею физическое явление. И, наоборот, если малые возмущения начальных условий мало изменяют решения на всем промежутке их существования, то соответствующую математnческую модель следует признать удачной.

Обыкновенным дифференциальным уравнениемn–го порядканазывается уравнение вида

F (x, y(x), y '(x), y ''(x), … , y⁽ⁿ⁾(x)) = 0, где F — известная функция (n + 2)-х переменных, x — независимая переменная из интервала (a,b), y(x) — неизвестная функция. Число n называется порядком уравнения.

ОДУ 1порядка

Уравнением с разделенными переменными называется дифференциальное уравнение вида f(x)dx + g(y)dy = 0 с непрерывными функциями f(х) и g(y).

Однородным уравнением первого порядка называется уравнение вида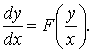

Линейным дифференциальным уравнением первого порядка называется уравнение вида 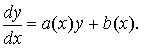Здесь a(x) и b(x) — известные, непрерывные на [a;b] функции.

Уравнением Бернулли называется уравнение первого порядка вида 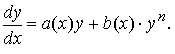Здесь a(x) и b(x) — известные, непрерывные на [a;b] функции, n > 1.

Уравнение M(x, y)dx + N(x, y)dy = 0 называется уравнением в полных дифференциалах, если выражение в левой части уравнения является дифференциалом некоторой функции двух переменных F(x, y), т.е. если dF(x, y) = M(x, y)dx + N(x, y)dy. Тогда F(x, y) = C — общий интеграл уравнения. Здесь C — произвольная постоянная.

ОДУ n-ого порядкаЕсли дифференциальное уравнение F(x, y, y ',..., y⁽ⁿ⁾ ) = 0 содержит производную неизвестной функции y = y(x) порядка n выше первого, то его называют уравнением n-го порядка и относят к уравнениям высших порядков.

Ме́тоды Ру́нге — Ку́тты— важное семейство численных алгоритмов решения обыкновенных дифференциальных уравнений и их систем. Данные итеративные методы явного и неявного приближённого вычисления были разработаны около 1900 года немецкими математиками К. Рунге и М. В. Куттой.

Метод Рунге — Кутты четвёртого порядка столь широко распространён, что его часто называют просто методом Рунге — Кутты.

Рассмотрим задачу Коши 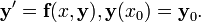Тогда приближенное значение в последующих точках вычисляется по итерационной формуле: 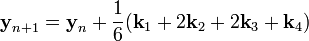Вычисление нового значения проходит в четыре стадии:

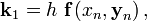
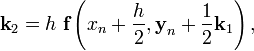
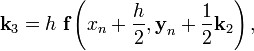
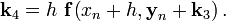где 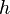— величина шага сетки по .

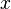Этот метод имеет четвёртый порядок точности, то есть суммарная ошибка на конечном интервале интегрирования имеет порядок 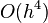(ошибка на каждом шаге порядка ).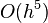