И координат точек опорной сети
КУРСОВАЯ РАБОТА
ИНЖЕНЕРНАЯ ГЕОДЕЗИЯ И ГЕОИНФОРМАТИКА
СОЗДАНИЕ ГЕОДЕЗИЧЕСКОГО ОБОСНОВАНИЯ
И РАЗБИВКА ОПОР МОСТОВОГО ПЕРЕХОДА
Вариант № 43
Выполнил студент Мартынова О.В. Группа сСМТ 21
Фамилия И.О.
Проверил преподаватель Глухов А.Т.
Фамилия И.О.
Задание выдано
“16” февраля 2013 года
Срок сдачи “25” мая 2013 года
Студент _____________ ___________
Подпись Фамилия И.О.
Преподаватель __________ __________
Подпись Фамилия И.О.
Саратов 2013
Задание 1
Выполнить уравнивание углов, вычисление сторон
и координат точек опорной сети
1. Исходные данные. Плановое обоснование для разбивки на местности опор мостового перехода выполнено методом мостовой триангуляции. Схема сети триангуляции в виде геодезического четырехугольника представлена на рис. 1. Опорные точки 5, 6, 11 и 12 закреплены на местности по типу временных геодезических знаков в виде столиков для установки теодолита. На каждой точке измерены углы теодолитом 3Та 5 р. Их значения и номера (№ 1, 2, 3, 4, 5, 6, 7, 8), а также обозначения сторон (A, B, C, D, E, F) указаны на рис. 1. Средняя квадратическая погрешность измерения одного угла составляет m = ± 5".
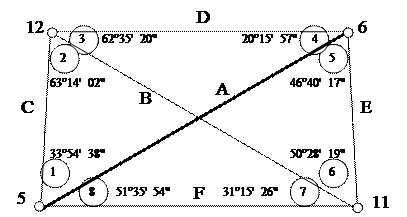 |
Рис. 1. Схема опорной геодезической сети
В соответствии с вариантом решения задачи заполнить соответствующие графы табл. 1: дирекционный угол линии 5-6 (α56), длину линии A (d56), координаты опорной точки 6 (X6, Y6) и отметку репера № 2914 (H2914).
Таблица 1
Исходные данные, вариант №43
| № опор-ной точки | Дирекцион-ный угол, α56 ° ' " | Длина стороны, d56, м | Координаты, м | Отметка, H, м | № опор-ной точки | |
| X | Y | |||||
| 101 55 15,0 | 498,483 | |||||
| 5354,982 | 6563,746 | |||||
| Рп | 126,349 | Рп |
Примечание. Заполнение табл. 1 выполнить в клетках помеченных знаком”*”
2. Выполнить уравнивание и оценку точности измерения горизонтальных углов (табл. 2), вычислить длину сторон геодезического четырехугольника (табл. 3) и координат точек опорной сети (табл. 4). Для вычисления координат точек опорной сети (см. табл. 4) принять левые углы по ходу в соответствии с нумерацией точек (5→6→12→11→5→6, см. рис.1).
Таблица 2
Уравнивание углов опорной геодезической сети
| № угла | Углы измеренные, β ° ' " | Суммы (1+2) (5+6) (3+4) (7+8) | Невязки f1= β(1+2) - β(5+6) f2= β(3+4) - β(7+8) | Поправки | Углы исправленные, (уравновешенные), β ° ' " | № угла | ||
| По условиям β(1+2) = β(5+6) β(3+4) = β(7+8). ± f1/4 ± f2/4 | По условию ∑β(1-8) = ∑βт -δ/8 | Суммар-ные поправки, v" | ||||||
| 33°54' 38" | 97 08 40 | f1 =+ 4 | -1 | 0.875 | -0.125 | 33 54 37.9 | ||
| 63°14' 02" | -1 | 0.875 | -0.125 | 63 14 01.9 | ||||
| 46°40' 17" | 97 08 36 | +1 | 0.875 | +1.875 | 46 40 18.9 | |||
| 50°28' 19" | +1 | 0.875 | +1.875 | 50 28 20.9 | ||||
f1(доп)=±mt 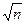 = = ± 5*2 = = ± 5*2 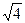 = ±20 = ±20 | ||||||||
| 62°35' 20" | 82 51 17 | f2 =-3 | +0.75 | 0.875 | +1.625 | 62 35 21.6 | ||
| 20°15' 57" | +0.75 | 0.875 | +1.625 | 20 15 58.6 | ||||
| 31°15' 26" | 82 51 20 | -0.75 | 0.875 | 0.125 | 31 15 26.1 | |||
| 51°35' 54" | -0.75 | 0.875 | 0.125 | 51 35 54.1 | ||||
f2(доп)=±mt 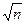 = = ±5*2 = = ±5*2 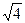 = ±20 = ±20 | ||||||||
| ∑β(1-8) | 359 59 53 | ∑β(1-8)=360 | ||||||
δф = ∑β(1-8) - ∑βт δф = -0 00 07 δдоп = ± m t 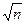 = ±5*2 = ±5*2 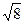 = ± 28 = ± 28 |
Таблица 3
Решение треугольников (вычисление длин линий опорной геодезической сети)
| № точки | № угла | Уравновешенные углы ° ' " | Sin углов | Вычисленная длина сторон, d, м | Поправки в длины сторон, δd, м | Исправленная длина сторон, d, м | Обозначение сторон |
| 6+7 | 81 43 45.0 | 0.991368757 | А | ||||
| 51 35 54 | 0.793176225 | E | |||||
| 46 40 17 | F | ||||||
| ∑β | |||||||
| 2+3 | 125 49 22.0 | A | |||||
| 20 15 57 | C | ||||||
| 97 08 40 | D | ||||||
| ∑β | |||||||
| 50 28 19 | D | ||||||
| 4+5 | 66 56 14.0 | B | |||||
| 62 35 20 | E | ||||||
| ∑β |
 | |||||
 | |||||
| |||||
|

|
Вычисление координат точек опорной геодезической сети
| № то-чек | Углы исправ-ленные ° ' " | Дирек-ционные углы ° ' " | Исправ-ленные стороны d, м | Вычисленные прирашения координат, м | Поправки, м | Исправленные приращения координат, м | Координаты, м | № то-чек | |||||
| ∆X | ∆Y | δX | δY | ∆X | ∆Y | X | Y | ||||||
| ∑β | ∑d = | ∑∆X= | ∑∆Y= | ∑ δX= | ∑δY= | ∑∆X = | ∑∆Y= | ||||||
| ∑βт | fx = | fy = | |||||||||||
| f(абс) = ± | |||||||||||||
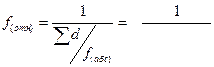 | f(отн, доп) = 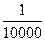 | ||||||||||||
Задание 2
