ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 13
1. Опишите, какие числа в ЭВМ представляют в естественной форме? Обоснуйте особенности выполнения арифметических действий над числами в естественной форме. Приведите примеры выполнения операций сложения и вычитания над целыми числами, представленными: а) одним байтом; б) двумя байтами.
Машинным изображением числа называют его представление в разрядной сетке ЭВМ. В вычислительных машинах применяются две формы представления чисел:
естественная форма или форма с фиксированной запятой (точкой);
нормальная форма или форма с плавающей запятой (точкой);
Пример:
(естественная форма) 452,34 = 452340*10-3 = 0,0045234*105 = 0,45234*103(нормальная форма)
Всякое десятичное число, прежде чем оно попадает в память компьютера, преобразуется по схеме:
X10 → X2 = M1 × [102]r
После этого осуществляется ещё одна важная процедура:
мантисса с её знаком заменяется кодом мантиссы с её знаком;
порядок числа с его знаком заменяется кодом порядка с его знаком.
Указанные коды двоичных чисел - это образы чисел, которые и воспринимают вычислительные устройства. Каждому двоичному числу можно поставить в соответствие несколько видов кодов.
Существуют следующие коды двоичных чисел:
Прямой код;
Обратный код;
Дополнительный код.
Последние две формы применяются особенно широко, так как позволяют упростить конструкцию арифметико-логического устройства компьютера путем замены разнообразных арифметических операций операцией сложения.
Естественная форма
В форме с фиксированной запятой в разрядной сетке выделяется строго определенное число разрядов для целой и для дробной частей числа. Левый (старший) разряд хранит признак знака (0 – "+", 1 – "-") и для записи числа не используется.
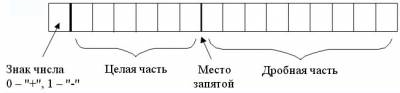
Сама запятая никак не изображается, но ее место строго фиксировано и учитывается при выполнении всех операций с числами. Независимо от положения запятой в машину можно вводить любые числа, т.к.
A = [A] · KА,
где А – произвольное число, [A] – машинное изображение числа в разрядной сетке, KА - масштабный коэффициент.
Естественная форма числа в неявном, условном виде реализуется формулой:
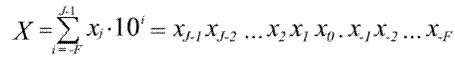
т.е. число записывается только с помощью набора значащих цифр xj без явного указания их весов и знаков сложения между ними. Отсчет ведется от точки, которая обычно фиксируется между целой и дробной частями числа.
С фиксированной запятой числа изображаются в виде последовательности цифр с постоянным для всех чисел положением запятой, отделяющей целую часть от дробной(например, 32,54; 0,0036; –108,2). Форма представления чисел с фиксированной запятой упрощает аппаратную реализацию ЭВМ, уменьшает время выполнения машинных операций, однако при решении задач на машине необходимо постоянно следить за тем, чтобы все исходные данные, промежуточные и окончательные результаты находились в допустимом диапазоне представления. Если этого не соблюдать, то возможно переполнение разрядной сетки, и результат вычислений будет неверным. От этих недостатков в значительной степени свободны ЭВМ, использующие форму представления чисел с плавающей точкой, или нормальную форму. В современных компьютерах форма представления чисел с фиксированной запятой используется только для целых чисел.
Прямой код
Представление числа в привычной форме "знак"-"величина", при которой старший разряд ячейки отводится под знак, а остальные - под запись числа в двоичной системе, называется прямым кодом двоичного числа. Например, прямой код двоичных чисел 1001 и -1001 для 8-разрядной ячейки равен 00001001 и 10001001 соответственно.
Положительные числа в ЭВМ всегда представляются с помощью прямого кода. Прямой код числа полностью совпадает с записью самого числа в ячейке машины. Вообще, положительные числа в прямом, обратном и дополнительном кодах изображаются одинаково — двоичными кодами с цифрой 0 в знаковом разряде.
Например,

Прямой код отрицательного числа отличается от прямого кода соответствующего положительного числа лишь содержимым знакового разряда. Но отрицательные целые числа не представляются в ЭВМ с помощью прямого кода, для их представления используется так называемый дополнительный код.
Прямой код двоичного числа(а это либо мантисса, либо порядок) образуется по такому алгоритму:
Определить данное двоичное число - оно либо целое (порядок), либо правильная дробь (мантисса).
Если это дробь, то цифры после запятой можно рассматривать как целое число.
Если это целое и положительное двоичное число, то вместе с добавлением 0 в старший разряд число превращается в код. Для отрицательного двоичного числа перед ним ставится единица.
Например,
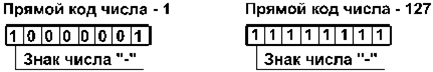
Обратный код
Обратный код положительного двоичного числа совпадает с прямым кодом.Для отрицательного числа все цифры числа заменяются на противоположные (1 на 0, 0 на 1), а в знаковый разряд заносится единица.
Например,

Дополнительный код
Дополнительный код положительного числа равен прямому коду этого числа. Дополнительный код отрицательного числа m равен 2k - |m|, где k - количество разрядов в ячейке.Также дополнительный код отрицательного числа образуется путём прибавления 1 к обратному коду.
При представлении целых чисел со знаком старший (левый) разряд отводится под знак числа, и под собственно число остаётся на один разряд меньше.
Алгоритм получения дополнительного кода отрицательного числа:
модуль отрицательного числа представить прямым кодом в k двоичных разрядах;
значение всех бит инвертировать:все нули заменить на единицы, а единицы на нули(таким образом, #получается k-разрядный обратный код исходного числа);
к полученному обратному коду прибавить единицу.
Дополнительный код используется для упрощения выполнения арифметических операций. Если бы вычислительная машина работала с прямыми кодами положительных и отрицательных чисел, то при выполнении арифметических операций следовало бы выполнять ряд дополнительных действий. Например, при сложении нужно было бы проверять знаки обоих операндов и определять знак результата. Если знаки одинаковые, то вычисляется сумма операндов и ей присваивается тот же знак. Если знаки разные, то из большего по абсолютной величине числа вычитается меньшее и результату присваивается знак большего числа. То есть при таком представлении чисел (в виде только прямого кода) операция сложения реализуется через достаточно сложный алгоритм. Если же отрицательные числа представлять в виде дополнительного кода, то операция сложения, в том числе и разного знака, сводится к из поразрядному сложению.
Для компьютерного представления целых чисел обычно используется один, два или четыре байта, то есть ячейка памяти будет состоять из восьми, шестнадцати или тридцати двух разрядов соответственно.
Например,
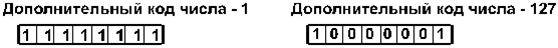
А) (+95)-(+127)=-32 01011111+10000000 + 1 = 11011111=-32
+95 обратный код инкремент
(+95)+(+127)=222; 256-222=34 дополнительный код отрицательного числа (-34) 01011111+01111111=-34
+95 +127
Б) Аналогично для 2ух байтовых
2. Порядок назначения IP-адресов. Назначение адресов автономной сети. Централизованное распределение адресов. Адресация и технология CIDR.
