Центральная предельная теорема теории вероятностей.

Моделирование непрерывных случайных величин на ЭВМ.

Цель работы. Моделирование различных типов непрерывных случайных величин в среде SciLab на основе равномерно распределённой на отрезке [0,1] случайной величины.

1. Моделирование непрерывно распределённой случайной величины методом обратной функции

Задание III

Моделирование потока Пуассона

1) Задать экспоненциальное распределение с плотностью вероятности 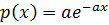– степенная функция (значения параметра «a» студент выбирает самостоятельно).

2) Построить моделирующий алгоритм в виде отдельной подпрограммы на основе метода обратной функции.

3) Вычислить оценку математическое ожидание и дисперсию распределения.

4) Построить гистограмму распределения для различных значений параметра «a».

Решение:

function v=Puass() a=0.04; y=rand(); v=-log(1-y)/a;endfunctions=Puass()M=100000;data=zeros(M);for i=1:1:M data(i)= Puass();endhistplot(50,data)Mv=0;for i=1:1:M Mv=Mv+data(i);endMv2=0;for i=1:1:M Mv2=Mv2+(data(i))^2;endDv=0;Dv=Mv2-(Mv*Mv);endMv=Mv/M

Для M =100000:

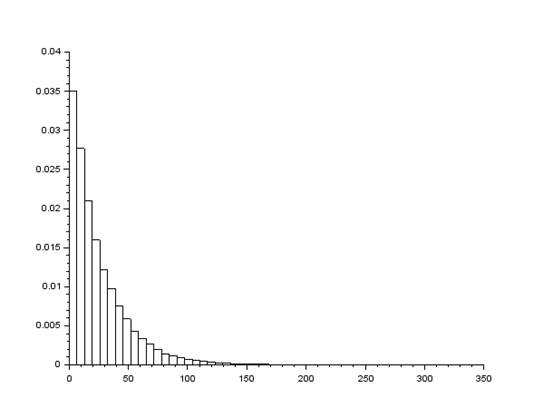
Для M =1000:

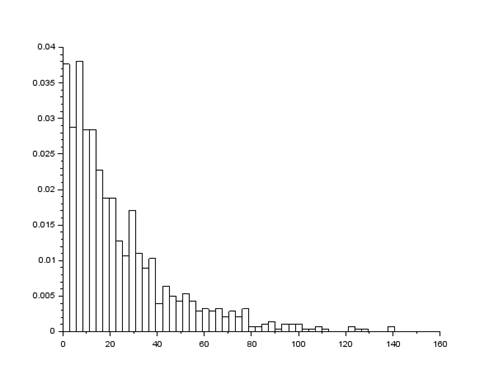
Моделирование нормально распределённой величины на основе центрально предельной теоремы.

Нормальным называют закон распределения вероятностей непрерывной случайной величины, который описывается функцией распределения

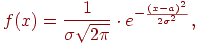Где a - математическое ожидание случайной величины;

σ-среднее квадратичное отклонение нормального распределения.

График функции распределения называют нормальной кривой (кривой Гаусса).

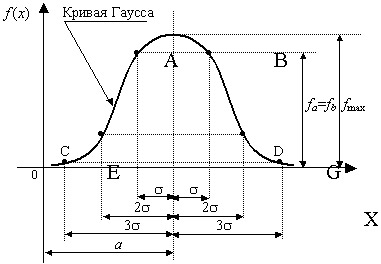
ожидания не превысит утроенного среднего квадратичного отклонения, равна 0,9973. Это свойство кривой Гаусса называется "правило трех сигм".

Площадь ограниченная нормальной кривой и осью X, равна единице.

Нормальное распределение с произвольными параметрами а и , т. е. описываемое функцией

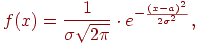
называется общим нормальным распределением.

Нормальное распределение с параметрами и , т. е. описываемое функцией

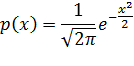
называется нормированным распределением. Чтобы получить нормированное распределение из произвольного необходимо выполнить преобразование

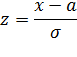
Центральная предельная теорема теории вероятностей.

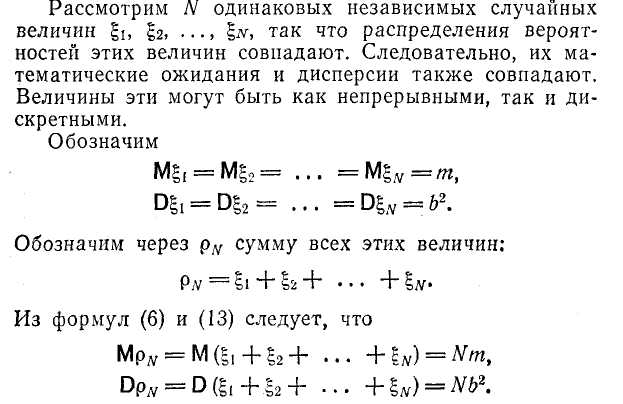
Полученная случайная величина близка к нормальному с параметрами

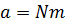
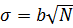
Согласно центральной предельной теореме, при сложении достаточно большого независимых случайных величин с произвольным законом распределения получается случайная величина, распределенная по нормальному закону. Опыт показывает, что при сложении всего шести (k=6) случайных величин равномерно распределенных на интервале [0,1], получается случайная величина, которая с точностью, достаточной для большинства прикладных задач, может считаться нормальной.

Рассмотрим метод аппроксимации нормально распределенной случайной величины Х, основанный на использовании двенадцати (k=12) равномерно распределенных случайных величин.

Алгоритм метода:

1. Сложить N равномерно распределенных псевдослучайных чисел y_i.

2. Пронормировать полученную сумму, т.е. получить случайную величину T с М(Т)=0 и , где Т – нормально распределенная случайная величина.

3. Результат привести в соответствие с заданным математическим ожиданием и среднеквадратичным отклонением .

Задание IV

1) Задать нормальное распределение с параметрами a и σ (значения параметров студент выбирает самостоятельно).

2) Построить моделирующий алгоритм на основе центральной предельной теоремы в виде отдельной функции.

3) Вычислить математическое ожидание и дисперсию распределения.

4) Построить гистограмму распределения для различных значений параметров распределения.

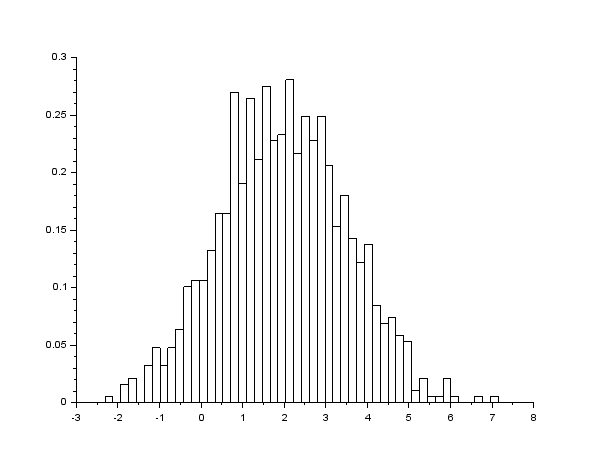
a=4; sigma = 0.63;function v=Rand_n(a, sigma) N=24 ro=0 for i=1:1:N ro=ro+rand() end Mro=N*0.5; Dro=N*1/12; tau=(ro-Mro)/sqrt(Dro); v=tau*sigma+a;endfunctionM=100000;data=zeros(M);for i=1:1:M data(i)= Rand_n(2,1.5);endhistplot(50,data)Mv=0;for i=1:1:M Mv=Mv+data(i);endMv=Mv/M;Mv2=0;for i=1:1:M Mv2=Mv2+(data(i))^2;endDv=0;Dv=Mv2/M-(Mv*Mv);

Для M = 100000:

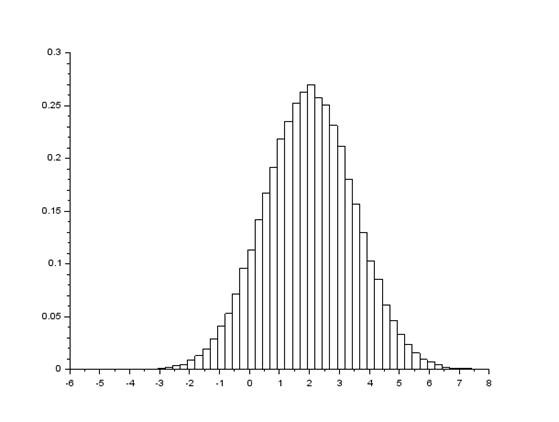
Для M = 1000: