Решение дифференциальных уравнений в приложении MathCAD

В приложении Mathcad решить дифференциальное уравнение можно, записав формулы выбранного метода. Например, пусть имеется дифференциальное уравнение: 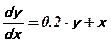, x₀=0 , y₀=1, h=0,1

Для решения уравнения методом Эйлера надо на рабочем поле Mathcad записать:

h:=0.1 n:=3 i:=0..n

x₀:=0 y₀:=1

x_i+1=x_i+h

y_i+1=y_i+h×(0.2×y_i+x_i)

Для получения численных значений записываются выражения:

x= y=

Имеются и встроенные функции для решения дифференциальных уравнений, например, встроенная функция rkfixed.

Чтобы решить систему дифференциальных уравнений, приведенную выше, можно записать:

x1:=1 x2:=1.3 Np:=20

y₀:=1 y₁:=0

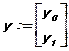
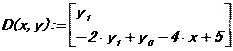
R:=rkfixed(y, x1, x2, Np, D)

Здесь x1, x2 – левая и правая границы интервала, на котором ищется решение; Np – число точек, в которых определяется решение; y_0, y₁ – начальные условия; D(x,y) – вектор правых частей системы. Для определения матрицы с решениями надо набрать R=

Можно также построить графики решения для различных значений i, характеризующие зависимость R(1,i)отR(0,i) и зависимость R(2,i)отR(0,i), то есть зависимость yотxи зависимостьzотx.