Подання дерев з використанням списків синів

Суть подання у тому, що створюється масив, розмірністю рівною кількістю вузлів дерева. Цей масив містить покажчики на списки, що містять синів для даного сайту.

Графічне подання:

Подання дерев з використанням покажчиків.

Суть подання у тому, що кожен вузол подається у вигляді окремої структури в динамічній пам'яті. У кожному вузлі є масив покажчиків на синів даного вузла.

Графічне подання.

Варіанти обходу дерев.

1. Прямий.

2. Зворотний.

3. Симетричний.

При проходженні в прямому порядку (тобто при прямому впорядкуванні) вузлів дерева 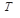спочатку відвідується корінь 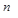, потім вузли піддерева 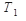, далі всі вузли піддерева , і таке інше. Останніми відвідуються вузли піддерева .

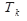При симетричному обході вузлів дерева 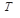спочатку відвідуються в симетричному порядку всі вузли піддерева 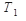, далі корінь 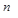, потім послідовно в симетричному порядку всі вузли піддерев .

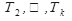Під час обходу в зворотному порядку спочатку відвідуються в зворотному порядку всі вузли піддерева 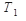, потім послідовно відвідуються всі вузли піддерев 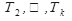, також у зворотному порядку, останнім відвідується корінь .

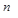Завдання для виконання лабораторної роботи №5.

1. Реалізувати дерево математичного виразу, реалізоване за допомогою списку синів. Зробити його обхід прямим методом. Підрахувати кількість вузлів дерева.

2. Реалізувати дерево математичного виразу, реалізоване за допомогою покажчиків. Зробити його обхід прямим методом. Підрахувати кількість вузлів дерева.

3. Реалізувати дерево математичного виразу, реалізоване за допомогою списку синів. Зробити його обхід зворотним методом. Підрахувати кількість вузлів дерева.

4. Реалізувати дерево математичного виразу, реалізоване за допомогою покажчиків. Зробити його обхід зворотним методом. Підрахувати кількість вузлів дерева.

5. Реалізувати дерево математичного виразу, реалізоване за допомогою списку синів. Зробити його обхід симетричним методом. Підрахувати кількість вузлів дерева.

6. Реалізувати дерево математичного виразу, реалізоване за допомогою покажчиків. Зробити його обхід симетричним методом. Підрахувати кількість вузлів дерева.

7. Реалізувати дерево математичного виразу, реалізоване за допомогою списку синів. Зробити його обхід прямим методом. Визначити глибину дерева.

8. Реалізувати дерево математичного виразу, реалізоване за допомогою покажчиків. Зробити його обхід прямим методом. Визначити глибину дерева.

9. Реалізувати дерево математичного виразу, реалізоване за допомогою списку синів. Зробити його обхід зворотним методом. Визначити глибину дерева.

10. Реалізувати дерево математичного виразу, реалізоване за допомогою покажчиків. Зробити його обхід зворотним методом. Визначити глибину дерева.

11. Реалізувати дерево математичного виразу, реалізоване за допомогою списку синів. Зробити його обхід симетричним методом. Визначити глибину дерева.

12. Реалізувати дерево математичного виразу, реалізоване за допомогою покажчиків. Зробити його обхід симетричним методом. Визначити глибину дерева.

Вимоги до звіту:

Звіт з лабораторної роботи повинен відповідати наступній структурі:

1. Словесна постановка задачі. У цьому підрозділі проводиться повний опис завдання. Описується суть завдання, аналіз вхідних в неї фізичних величин, район їх допустимих значень, одиниці їх вимірювання, можливі обмеження, аналіз умов при яких завдання має рішення (не має рішення), аналіз очікуваних результатів.

2. Математична модель. У цьому підрозділі вводяться математичні описи фізичних величин і математичний опис їх взаємодій. Мета підрозділу - представити вирішувану задачу в математичній формулюванні.

3. Алгоритм рішення задачі. У підрозділі описується розробка структури алгоритму, обгрунтовується абстракція даних, завдання розбивається на підзадачі. Приводится схема алгоритму або псевдокод. Вказується оцінка алгоритму.

4. Лістинг програми.

5. Контрольний тест. Підрозділ містить набори вихідних даних і отримані в ході виконання програми результати.

6. Висновки з лабораторної роботи.

Лабораторна робота №6

Тема: Знаходження найкоротшої відстані між двома вершинами графа методом Дейкстри.

Мета лабораторної роботи – закріплення теоретичного матеріалу, отримання практичних навичків реалізації алгоритма Дейкстри.

Орієнтований граф.

Орієнтований граф (або скорочено орграф) 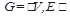складається з множени вершин 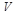і множени дуг 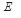. Вершини також називають вузлами, а дуги - орієнтованими ребрами. Дуга може бути подана у вигляді впорядкованої пари вершин , де вершина 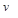- початок, а 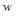- кінець дуги.

Графічне представлення.

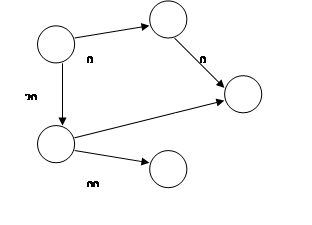Якщо ребрам графа відповідає певне число - вага ребра, то цей граф називається зваженим.

Варіанти представлення графів:

1. матріца суміжності;

2. список суміжності.