Теорема Котельникова В. А

Основы теории информации

1. Понятие информации, ее свойства, формы и виды.

Понятие информации является основополагающим понятием информатики. Любая деятельность человека представляет собой процесс сбора и переработки информации, принятия на ее основе решений и их выполнения. С появлением современных средств вычислительной техники информация стала выступать в качестве одного из важнейших ресурсов научно-технического прогресса.

Информация содержится в человеческой речи, текстах книг, журналов и газет, сообщениях радио и телевидения, показаниях приборов и т.д. Человек воспринимает информацию с помощью органов чувств, хранит и перерабатывает ее с помощью мозга и центральной нервной системы. Передаваемая информация обычно касается каких-то предметов или на самих и связана с событиями, происходящими в окружающем нас мире.

Термин информация происходит от латинского слова informatio, что означает разъяснение, осведомленность, изложение. Информация-сведения об объектах и явлениях окружающей среды, их параметрах, свойствах и состоянии, которые уменьшают имеющуюся о них степень неопределенности, неполноты знаний.

С понятием информации связаны такие понятия, как сигнал, сообщение и данные.

Сигнал представляет собой любой процесс, несущий информацию.

Сообщение – это информация, представленная в определенной форме и предназначенная для передачи.

Данные – это информация, представленная в формализованном виде и предназначенная для обработки ее техническими средствами, например, ЭВМ.

Любое информационное сообщение можно представить функцией X(t), характеризующей изменение во времени материально – энергетических параметров физической среды, в которой осуществляются информационные процессы.

Функция X(t) принимает любые вещественные значения в диапазоне изменения аргумента t. Если функция X(t) непрерывная, то имеет место «непрерывная» или аналоговая информация. Источником аналоговой информации являются различные природные объекты (например, температура и влажность воздуха), объекты технологических производственных процессов (давление и температура теплоносителя в контурах ядерного реактора) и т.д.

Если функция X(t) дискретна, то информационное сообщение имеет характер дискретных сообщений. Например, сигналы тревоги, передаваемые посредством световых и звуковых сообщений, языковые сообщения, передаваемые в письменном или звуковом виде, сообщения, передаваемые с помощью жестов.

Информация может быть входной, выходной и внутренней. Если система или объект воспринимает любую совокупность сигналов извне, то такая информация называется входной. Если же система или объект выдает в окружающую среду любую совокупность сигналов, то такая информация называется выходной. А, если система или объект хранит в себе любую совокупность сигналов, то такая информация называется внутренней.

2. Способы кодирования символьной, числовой, графической, звуковой, видео информации в ЭВМ.

Современный компьютер может обрабатывать числовую, текстовую, графическую, звуковую и видео информацию. Все эти виды информации в компьютере представлены в двоичном коде, т. е. используется алфавит мощностью два (всего два символа 0 и 1). Связано это с тем, что удобно представлять информацию в виде последовательности электрических импульсов: импульс отсутствует (0), импульс есть (1). Такое кодирование принято называть двоичным, а сами логические последовательности нулей и единиц - машинным языком.

Вид информации	Двоичный код
Числовая
Текстовая
Графическая
Звуковая
Видео

Каждая цифра машинного двоичного кода несет количество информации равное одному биту. Данный вывод можно сделать, рассматривая цифры машинного алфавита, как равновероятные события. При записи двоичной цифры можно реализовать выбор только одного из двух возможных состояний, а, значит, она несет количество информации равное 1 бит. Следовательно, две цифры несут информацию 2 бита, четыре разряда --4 бита и т. д. Чтобы определить количество информации в битах, достаточно определить количество цифр в двоичном машинном коде. Кодирование текстовой информации В настоящее время большая часть пользователей при помощи компьютера обрабатывает текстовую информацию, которая состоит из символов: букв, цифр, знаков препинания и др. Традиционно для того чтобы закодировать один символ используют количество информации равное 1 байту, т. е. I = 1 байт = 8 бит. При помощи формулы, которая связывает между собой количество возможных событий К и количество информации I, можно вычислить сколько различных символов можно закодировать (считая, что символы - это возможные события): К = 2I = 28 = 256, т. е. для представления текстовой информации можно использовать алфавит мощностью 256 символов. Суть кодирования заключается в том, что каждому символу ставят в соответствие двоичный код от 00000000 до 11111111 или соответствующий ему десятичный код от 0 до 255. Необходимо помнить, что в настоящее время для кодировки русских букв используют пять различных кодовых таблиц (КОИ - 8, СР1251, СР866, Мас, ISO), причем тексты, закодированные при помощи одной таблицы не будут правильно отображаться в другой кодировке. Наглядно это можно представить в виде фрагмента объединенной таблицы кодировки символов. Одному и тому же двоичному коду ставится в соответствие различные символы.

3. Системы счисления. Представление чисел в позиционных системах счисления.

Система счисления — символический метод записи чисел, представление чисел с помощью письменных знаков.

· Число — некоторая абстрактная сущность, мера для описания количества.

· Цифры — знаки, используемые для записи чисел.

Цифры бывают разные: самыми распространёнными являются арабские цифры, представляемые знаками от нуля (0) до девяти (9); менее распространены римские цифры, их можно встретить на циферблате часов или в обозначении века (XIX век).

Поскольку чисел гораздо больше чем цифр, то для записи числа обычно используется набор (комбинация) цифр. Только для небольшого количества чисел — для самых малых по величине — бывает достаточно одной цифры. Существует много способов записи чисел с помощью цифр, называемых системой счисления. Величина числа может зависеть от порядка цифр в записи, а может и не зависеть. Это свойство определяется системой счисления и служит основанием для простейшей классификации таких систем, что позволяет все системы счисления разделить на три класса (группы):

· позиционные;

· непозиционные;

· смешанные.

Позиционные системы счисления подробно рассмотрены ниже, после краткого обзора смешанных и непозиционных систем.

Денежные знаки — это пример смешанной системы счисления.

Сейчас в России используются монеты и купюры следующих номиналов: по 1, 5, 10, 50 копеек и по 1, 2, 5, 10, 50, 100, 500, 1000, 5000 рублей. Чтобы получить некоторую сумму в рублях, нужно использовать некоторое количество денежных знаков различного достоинства.

Предположим, что пылесос стоит 6379 рублей. Для покупки можно использовать шесть купюр по тысяче рублей, три купюры по сто рублей, одну пятидесятирублёвую купюру, две десятки, одну пятирублёвую монету и две монеты по два рубля. Если записать количество купюр или монет начиная с 1000 руб. и заканчивая одной копейкой, заменяя нулями неиспользуемые номиналы, то получится число 603121200000.

Если перемешать цифры в числе 603121200000, оно представит ложную цену пылесоса. Следовательно, такая запись относится к позиционным системам.

В непозиционных системах счисления величина числа не зависит от положения цифр в записи. Если к каждой цифре приписать знак номинала, то такие составные знаки (цифра + номинал) уже можно перемешивать, то есть такая запись являетсянепозиционной.

4. Преобразование аналоговой информации в дискретную. Теорема Котельникова.

Теорема Котельникова В. А.

В качестве достаточно универсальной модели сигнала принимается случайный процесс.

Пусть каждая из реализаций этого случайного процесса представляет функцию с ограниченным спектром ω ≤ ω_max = 2πƒ_max.

В этом случае для преобразования непрерывного сигнала в дискретно-непрерывный можно использовать теорему Котельникова.

В 1933 году Котельникова В.А. доказал, что сигнал, описываемый функцией с ограниченным спектром, полностью определяется дискретным рядом значений, отсчитанных через максимально допустимые интервалы времени

,

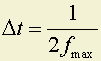где ƒ_max – максимальная частота в спектре сигнала.

Следовательно, если требуется передать сигнал, описываемый дискретной функцией ƒ(t) с ограниченным спектром, то достаточно передавать отдельные мгновенные значения, отсчитанные через конечный промежуток времени . По этим значениям непрерывный сигнал может быть полностью восстановлен на выходе системы: .

Это положение объясняется тем, что отсутствие высших гармоник в составе ƒ(t) накладывает ограничения на способы, которыми могут быть соединены каждые две соседние точки.

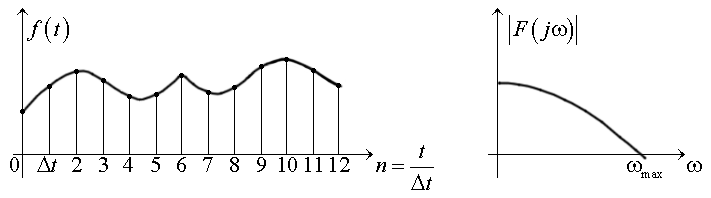
Рис. 9.3

Доказательство состоит в разложении функции ƒ(t) в особого рода ряд.

В общем случае

,

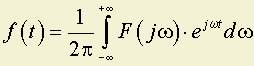где

.

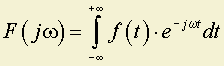В данном, частном случае имеем

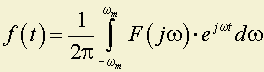
В момент времени

;

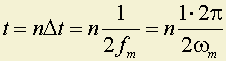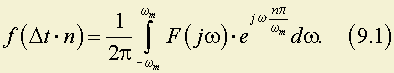
Функция же F(jω) на конечном промежутке (–ω_m; ω_m) может быть разложена в ряд Фурье по частотам следующим образом (путём её периодического продолжения с периодом 2ω_m на весь интервал частот ω от –∞ до ∞)

;
;

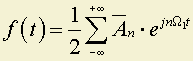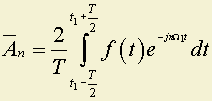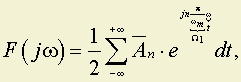
где

;


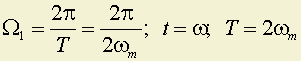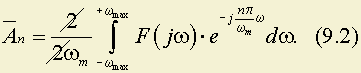
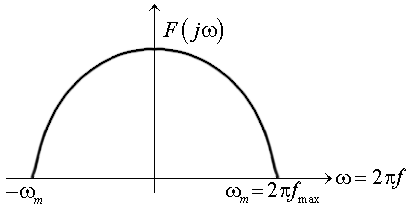
Рис. 9.4

Из сравнения (9.1) и (9.2) следует

.

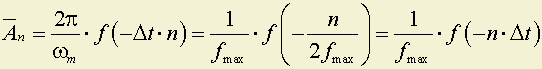Таким образом коэффициенты A_n пропорциональны значениям функции ƒ(t) в дискретные момента времени

.

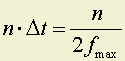Коэффициенты A_n полностью определяют F(jω), а последняя полностью определяет функцию ƒ(t). Следовательно, знание значений функции ƒ(t) в моменты временидостаточно для полного определения функции ƒ(t).

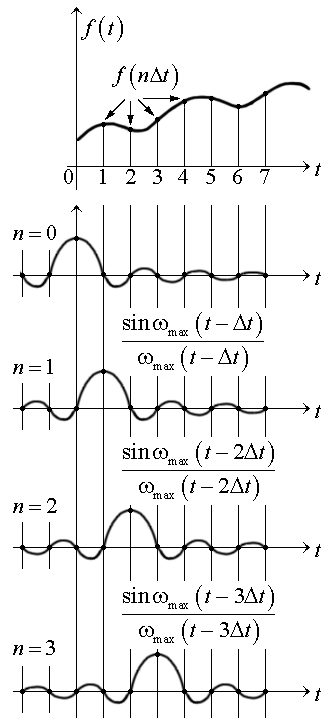
Рассмотрим теперь восстановление функции ƒ(t) по её значениям в моменты времени t_n.

F(jω) – периодическая;

ƒ(t) – в пределах 1-го периода.

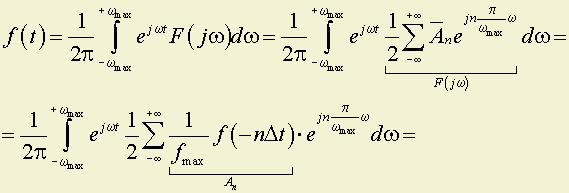
если заменить на f(nΔt), то изменится знак в e^–jnΔtω

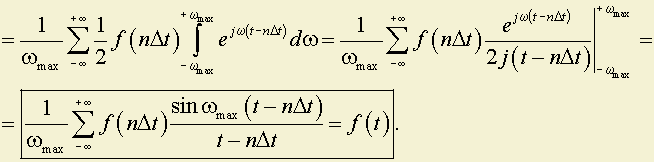
Восстановление идет по функции.

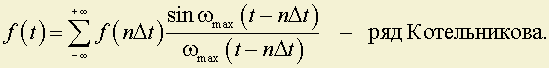
1. f(nΔt) – значения f(t) в моменты времени nΔt.

2. – функция, принимающая max = 1 в точке t = nΔt, а в остальных точках kΔt, где k ≠ n равна нулю, так как t = kΔt, то

.

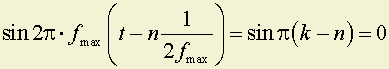Рассмотрим смысл этого выражения.

5. Основы передачи данных, каналы передачи информации, методы повышения помехозащищенности и помехоустойчивости передачи и приема данных.