Представление чисел в двоичной и десятичной системе счисления
Перевод из десятичной системы.
Пример: 999,3510=1111100111,010112
для целой части:
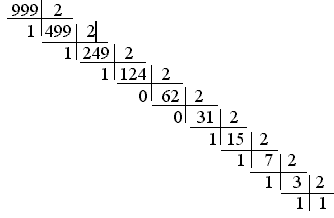
для дробной части:
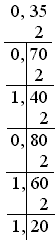
Действительно 21,75(10) = 2*101+1*100+7*10-1+5*10-2
10101,11(2)=1*24+ 0*23 + 1*22 + 0*21 + 1*20 + 1*2-1 + 1*2-2 = 16+4+1+0,5+0,25 = 21,75(10)
Из двоичной в десятичную.
В этом случае рассчитывается полное значение числа по формуле, причем коэффициенты ai принимают десятичное значение в соответствии с таблицей.
Пример. Выполнить перевод из двоичной системы счисления в десятичную числа 0,11012. Имеем:
0,11012 = 1*2-1 + 1*2-2 + 0*2-3 +1*2-4 = 0,5 + 0,25 + 0 + 0,0625 = 0,8125.
Расхождение полученного результата с исходным для получения двоичной дроби числом вызвано тем, что процедура перевода в двоичную дробь была прервана.
Таким образом, 0,11012 = 0,8125.
- Арифметические операции в различных системах исчисления.
Основной операцией, которая используется в цифровых устройствах при различных вычислениях, является операция алгебраического сложения чисел (сложения, в котором могут участвовать как положительные, так и отрицательные числа). Вычитание легко сводится к сложению путём изменения на обратный знака вычитаемого. Операции умножения и деления также выполняются с помощью операции сложения и некоторых логических действий. Поэтому именно с операции сложения начнём рассмотрения способов выполнения арифметических операций.
При записи кода числа знак числа будем представлять полужирными цифрами 0 (для положительных чисел) и 1 (для отрицательных чисел). Положение точки в числе показывать не будем.
Сложение положительных двоичных чисел. Выполнение этой операциипокажем на примере:
Переносы
Первое слагаемое N1 0 0 1 0 0 1
Второе слагаемое N2 +0 0 1 0 0 1
Сумма N = N1+N2 0 1 0 1 1 0
Цифры разрядов суммы N = N1+N2 формируются последовательно, начиная с младшего разряда. Цифра младшего разряда суммы образуется суммированием цифр младших разрядов слагаемых. При этом, кроме цифры разряда суммы, формируется цифра переноса в следующий, более старший разряд. Таким образом, в разрядах, начиная со второго, суммируются три цифры6 цифры соответствующего разряда слагаемых и перенос, поступающий в данный разряд из предыдущего.
Перенос равен 1 во всех случаях, когда результат суммирования цифр в разряде равен или больше р = 2 (р – основание системы счисления). При этом в разряд суммы записывается цифра, на р единиц (т.е. на две единицы) меньшая результата суммирования.
Умножение двоичных чисел. Операция умножения чисел, представленных в форме с фиксированной точкой, включает в себя определение знака и абсолютного значения произведения.
Определение знака произведения. Знаковый разряд произведения может быть получен суммированием знаковых разрядов сомножителей без формирования переноса (так называемым суммированием по модулю 2). Действительно, при совпадении цифр знаковых разрядов сомножителей (0 … и 0…, либо 1 … и 1…) их сумма по модулю 2 равна 0, т.е. соответствует знаковому разряду произведения двух сомножителей, имеющих одинаковые знаки; при несовпадении цифр знаковых разрядов эта сумма будет равна 1, что также соответствует знаковому разряду произведения двух сомножителей с разными знаками.
Определение абсолютного значения произведения. Абсолютное значение произведения получается путём перемножения чисел без учёта их знаков.
Произведём умножение чисел 11012 и 10112 .
1 1 0 1 множимое
х
1 0 1 1 множитель
1 1 0 1 1-е частичное произведение
1 1 0 1 2-е частичное произведение
0 0 0 0 3-е частичное произведение
1 1 0 1_______ 4-е частичное произведение
1 0 0 0 1 1 1 1 произведение
Деление двоичных чисел. Будем рассматривать операцию алгебраического сложения чисел, представленных в форме с фиксированной точкой. При этом выполнение операций содержит действия, связанные с определением частного, и действия, связанные с определением модуля частного. Знак частного может быть найден тем же приёмом, что и знак произведения в рассмотренной выше операции умножения с отделением знаковых разрядов. Поэтому ниже рассматривается только нахождение модуля частного. На примере эта операция выглядит так. Пусть после отделения знаковых разрядов модули делимого и делителя представляются соответственно числами а = 0,10010 и в = 0,10110.
Встречающуюся операцию вычитания числа заменим прибавлением числа -в, представленного в дополнительном коде (-в)доп = 1,01010.
а 0 , 1 0 0 1 0 0, 1 0 1 1 0
+ ____________
(-в)доп 1 , 0 1 0 1 0 с < 0 0, 1 1 0 1 0 частное





 с 1 , 1 1 1 0 0
с 1 , 1 1 1 0 0
Сдвиг влево 1 , 1 1 0 0 0
+
в 0 , 1 0 1 1 0 с > 0
 с 0 , 0 1 1 1 0
с 0 , 0 1 1 1 0
Сдвиг влево 0 , 1 1 1 0 1
+
(-в)доп 1 , 0 1 0 1 0 с > 0
 с 0 , 0 0 1 1 0
с 0 , 0 0 1 1 0
Сдвиг влево 0 , 0 1 1 0 0
+
(-в)доп 1 , 0 1 0 1 0 с < 0
 с 1 , 1 0 1 1 0
с 1 , 1 0 1 1 0
Сдвиг влево 1 , 0 1 1 0 0
+
в 0 , 1 0 1 1 0 с > 0

 с 0 , 0 0 0 1 0
с 0 , 0 0 0 1 0
сдвиг влево 0 , 0 0 1 0 0
+
(-в)доп 1 , 0 1 0 1 0 с < 0
 с 1 , 0 1 1 1 0
с 1 , 0 1 1 1 0
