Еория вероятностей и математическая статистика 5В070300, 5В060200

Раздел
1. Комбинаторика
2. Случайные события
3. Случайные величины
4. Математическая статистика
Итого

@@@ 1. Комбинаторика

$$$ 1 Е

Сколько двухзначных чисел можно составить из цифр 1,0,3. (без повторений)

А) 6

В) 12

С) 8

Д) 72

Е) 4

$$$ 3 E

Сколько трехзначных чисел можно составить из цифр 1,2,3. (без повторений)

А) 7

В) 12

С) 36

Д) 72

Е) 6

$$$ 5 Е

Сколько трехзначных чисел можно составить из цифр 1, 0, 2 (цифры не повторяются)

А) 7

В) 8

С) 6

Д) 7

Е) 4

$$$ 7 С

Сколько четырехзначных чисел можно составить из цифр 1, 2

А) 4

В) 8

С) 16

Д) 24

Е) 4

$$$ 9 Е

Сколько четырехзначных чисел можно составить из цифр 0, 2

А) 4

В) 6

С) 1

Д) 3

Е) 8

$$$ 11 В

Сколько трехзначных чисел можно составить из четных цифр (цифры могут повторяться )

А) 150

В) 100

С) 200

Д) 300

Е) 125

$$$ 12 В

Сколько двузначных чисел (цифры не повторяются) можно составить из цифр 1,2,3,4,5

А) 60

В) 20

С) 40

Д) 25

Е) 30

$$$ 15 А

Сколько трехзначных чисел можно составить из цифр 2,3,4,5 ( цифры не повторяются )

А) 24

В) 26

С) 28

Д) 32

Е) 36

$$$ 17 В

Сколькими способами можно выбрать 3 детали из ящика, содержашего 10 стандартных и 10 нестандартных, чтобы среди отобранных оказалась 1 стандартная.

А) 390

В) 450

С) 350

Д) 320

Е) 422

$$$ 19 D

Сколькими способами можно выбрать 5 шаров из урны , содержащей 6 красных и 4 белых шара, так чтобы среди отобранных было 2 красных

А) 70

В) 80

С) 90-

Д) 60

Е) 100

$$$ 21 С

В ящике 15 деталей, из которых 10 бракованных. Сколькими способами можно выбрать 7 деталей, чтобы среди них оказалось 3 бракованных.

А) 340

В) 320

С) 600

Д) 700

Е) 640

$$$ 23 Е

В ящике 20 деталей, из которых 15 бракованных. Сколькими способами можно выбрать 4 деталей, чтобы среди них оказалось 2 бракованных.

А) 2800

В) 3200

С) 1060

Д) 1040

Е) 1050

$$$ 25 Е

В ящике 20 деталей, из которых 15 бракованных. Сколькими способами можно выбрать 2 детали, чтобы среди них оказалось хотя бы одна бракованная.

А) 170

В) 132

С) 175

Д) 185

Е) 180

$$$ 27 D

Сколько различных перестановок можно сделать из букв слова ТОПОР?

А)120

В) 80

С) 720

Д) 60

Е) 100

$$$ 29 С

Сколько различных перестановок можно сделать из букв слова РОТОР?

А)120

В) 80

С) 30

Д) 60

Е) 100

$$$ 31 С

Сколько различных перестановок можно сделать из букв слова ПЕРЕПЕЛ?

А)120

В) 80

С) 420

Д) 60

Е) 200

$$$ 33 С

Сколько различных перестановок можно сделать из букв слова ЗОЛОТО?

А) 360

В) 80

С) 120

Д) 60

Е) 100

$$$ 35 С

Сколько различных перестановок можно сделать из букв слова САХАРА?

А) 160

В) 180

С) 120

Д) 140

Е) 100

$$$ 37 А

Сколькими способами могут разместиться в один ряд 5 человек?

А) 120

В) 25

С) 24

Д) 16

Е) 64

$$$ 35 А

Сколькими способами могут встать в очередь в кассу 3 человека?

А) 6

В) 8

С) 9

Д) 6

Е) 4

$$$ 39 А

Сколькими способами могут встать в очередь в кассу 4 человека?

А) 24

В) 80

С) 16

Д) 8

Е) 4

$$$ 41 В

Сколькими способами можно взять из урны, содержащей 20 шаров, 2 шара?

А) 240

В) 190

С) 120

Д) 164

Е) 140

$$$ 43 С

В ящике 12 деталей. Сколькими способами можно взять из ящика 4 детали для проверки?

А) 240

В) 380

С) 495

Д) 364

Е) 440

$$$ 45 Е

Сколькими способами можно взять из колоды 3 карты?

А) 6224

В) 3538

С) 5449

Д) 6236

Е) 7140

$$$ 45 В

Сколькими способами можно взять из колоды 3 карты, чтобы среди них оказалось 2 туза?

А) 122

В) 192

С) 144

Д) 236

Е) 140

$$$ 47 Д

Сколькими способами можно взять из колоды 5 карт, чтобы среди них оказалось 3 дамы?

А) 1822

В) 1092

С) 1644

Д) 1984

Е) 1740

$$$ 49 С

Сколькими способами можно взять из колоды 4 карты, чтобы среди них оказалось 2 дамы, 2 туза?

А) 52

В) 64

С) 36

Д) 16

Е) 24

$$$ 51 Е

Сколькими способами можно взять из колоды 6 карт, чтобы среди них оказалось 2 дамы, 2 валета, 1 король?

А) 2022

В) 2304

С) 3044

Д) 3004

Е) 3456

$$$ 53 Д

Сколькими способами можно взять из колоды 6 карт, чтобы среди них оказалось 2 дамы, 2 валета, 2 туза?

А) 100

В) 240

С) 160

Д) 216

Е) 256

$$$ 55 Е

Сколькими способами можно взять из колоды 4 карты, чтобы среди них оказалось 2 дамы, 1 валет?

А) 610

В) 524

С) 520

Д) 616

Е) 672

$$$ 57 В

Сколькими способами можно взять из колоды 6 карт, чтобы среди них оказалось 2 дамы, 4 валета?

А) 10

В) 6

С) 4

Д) 16

Е) 8

$$$ 59 Е

В урне 8 белых, 12 синих и 4 красных шаров. Сколькими способами можно взять из урны 3 шара, чтобы среди них оказалось 1 белый, 1синий и 1 красный шары?

А) 710

В) 824

С) 420

Д) 360

Е) 384

$$$ 61 В

Вычислить ?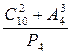

А)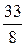

В)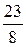

С)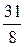

Д)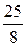

Е) 10

$$$ 63 С

Вычислить ?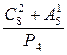

А)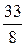

В)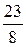

С)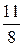

Д)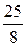

Е) 10

$$$ 64 В

Вычислить ?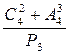

А) 12

В) 5

С) 10

Д)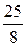

Е) 10

$$$ 65 А

Вычислить ?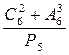

А)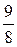

В)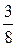

С)

Д)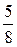

Е) 10

$$$ 67 Е

Вычислить ?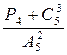

А) 2,8

В) 2,5

С) 2,5

Д) 10

Е) 1,7

$$$ 69 А

Вычислить ?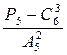

А) 5

В) 10

С) 2

Д) 4

Е) 10

$$$ 70 Е

Вычислить ?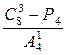

А) 5

В) 10

С) 2

Д) 4

Е) 8

@@@ 2. Случайные события

$$$ 1 Е

Найти вероятность того, что при бросании игральной кости один раз появится 5 очков

А) 1\5

В)2\15

С) 1\36

Д) 7\36

Е) 1\6

$$$ 3 Е

Найти вероятность того, что при бросании двух игральных костей шестерка появится хотя бы один раз

А) 1\36

В) 7\36

С) 1

Д) 0

Е) 11\36

$$$ 5 А

Найти вероятность того, что при бросании двух игральных костей на обеих выпадет нечетное число очков

А) 1\4

В) 1\2

С) 1

Д) 0

Е) 3\4

$$$ 7 А

Найти вероятность того, что при бросании двух игральных костей сумма очков будет равна 5

А) 1\9

В) 1\18

С) 1\12

Д) 1\10

Е) 1\5

$$$ 9 А

Найти вероятность того, что при бросании двух игральных костей сумма очков будет равна 9.

А) 1\9

В) 1\18

С) 1\12

Д) 1\10

Е) 1\5

$$$ 11 В

Найти вероятность того, что при бросании двух игральных костей сумма очков будет равна 10, а разность двум.

А) 1\9

В) 1\18

С) 1\12

Д) 1\10

Е) 1\5

$$$ 13 С

Найти вероятность того, что при бросании двух игральных костей сумма очков будет не превышает 7.

А) 1\9

В) 5\18

С) 7\12

Д) 1\10

Е) 1\5

$$$ 15 С

Найти вероятность того, что при бросании двух игральных костей хотя бы на одной выпадет 4 очка.

А) 1\9

В) 5\36

С) 11\36

Д) 1\10

Е) 10\36

$$$ 17 B

В урне 15 шаров, из них 5 белых. Найти вероятность того, что наудачу взятый шар не белый

А) 1\3

В) 2\3

С) 1

Д) 0

Е) 7\8

$$$ 19 C

В группе 18 девушек и 6 юношей

Разыгрывается один билет в театр. Какова вероятность того, что его получит юноша.

А) 1\2

В) 1\3

С) 1\4

Д) 1\5

Е) 1

$$$ 21 С

Найти вероятность того, что при бросании двух игральных костей сумма очков будет не превышает 4.

А) 1\9

В) 1\18

С) 1\6

Д) 1\10

Е) 1\5

$$$ 23 С

В урне 7 шаров, из них 4 белых. Найти вероятность того, что все три отобранные шара белые.

А)1\35

В) 0

С) 4\35

Д) 1

Е) 7\35

$$$ 25 E

В ящике 10 деталей, из них 6 бракованных. Найти вероятность того, что из двух отобранных хотя бы одна бракованная.

А) 2\15

В) 0

С) 1

Д) 7\15

Е) 13\15

$$$ 27 С

В группе 8 девушек и 6 юношей

Разыгрывается два билета в театр. Какова вероятность того, что его получат юноши.

А)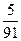

В)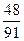

С)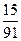

Д)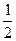

Е) 0

$$$ 29 А

Студент знает 12 вопросов из 20 вопросов программы. Найти вероятность, что он знает оба вопроса, из двух заданных.

А)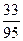

В)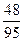

С)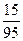

Д)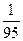

Е) 0

$$$ 31 С

Студент знает 12 вопросов из 20 вопросов программы. Найти вероятность, что он не знает оба вопроса, из двух заданных.

А)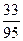

В)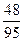

С)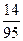

Д)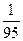

Е) 0

$$$ 33 А

Студент знает 10 вопросов из 20 вопросов программы. Найти вероятность, что он знает три вопроса, из трех заданных.

А)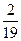

В)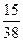

С)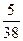

Д)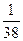

Е)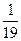

$$$ 35 С

Студент знает 10 вопросов из 20 вопросов программы. Найти вероятность, что он знает только1 вопрос, из трех заданных.

А)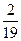

В)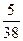

С)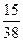

Д)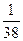

Е)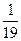

$$$ 37 Д

Студент знает 10 вопросов из 20 вопросов программы. Найти вероятность, что он знает хотя бы один вопрос, из трех заданных.

А)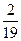

В)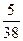

С)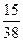

Д)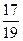

Е)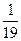

$$$ 39 Д

Найти вероятность того, что из двух отобранных карт из колоды (36 карт) только один будет туз.

А)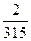

В)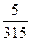

С)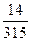

Д)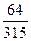

Е)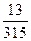

$$$ 41 А

В группе 15 студентов, из них 7 девушек. Найти вероятность того, что из трех отобранных студентов все девушки.

А)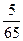

В)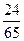

С)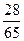

Д)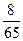

Е)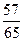

$$$ 43 С

В группе 15 студентов, из них 7 девушек. Найти вероятность того, что из трех отобранных студентов только 1 девушка.

А)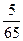

В)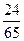

С)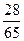

Д)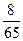

Е)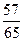

$$$ 45 Е

В группе 15 студентов, из них 7 девушек. Найти вероятность того, что из трех отобранных студентов хотя бы одна девушка.

А)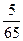

В)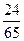

С)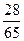

Д)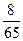

Е)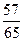

$$$ 47 C

Два стрелка стреляют по мишени. Вероятность попадания первым 0.5, вторым 0.4. Найти вероятность того, что при одном залпе в мишень попадет только один стрелок.

А) 0.2

В) 0.3

С) 0.5

Д) 0.4

Е) 0.7

$$$ 49 D

Два стрелка стреляют по мишени. Вероятность попадания первым 0.5, вторым 0.4.Найти вероятность того, что при одном залпе в мишень попадет хотя бы один стрелок

А) 0.1

В) 0.5

С) 0.2

Д) 0.7

Е) 1

$$$ 51 D

Три стрелка независимо друг от друга стреляют по целям вероятность попадания в цель для первого стрелка равна 0,7 для второго равна 0,8 для третьего 0,9. Какова вероятность, что все стрелки промахнулись.

A) 0,504

B) 0,398

C) 0,092

D) 0,006

Е) 0,005

$$$ 53 В

Три стрелка независимо друг от друга стреляют по целям вероятность попадания в цель для первого стрелка равна 0,7 для второго равна 0,8 для третьего 0,9. Какова вероятность, что в мишень попадет два стрелка.

A) 0,504

B) 0,398

C) 0,092

D) 0,006

Е) 0,005

$$$ 55 В

Три стрелка независимо друг от друга стреляют по целям вероятность попадания в цель для первого стрелка равна 0,7 для второго равна 0,8 для третьего 0,9. Какова вероятность, что в мишень попадет хотя бы один стрелок.

A) 0,504

B) 0,994

C) 0,096

D) 0,006

Е) 0,005

$$$ 57 D

Три стрелка независимо друг от друга стреляют по целям вероятность попадания в цель для первого стрелка равна 0,6 для второго равна 0,5 для третьего 0,4. Какова вероятность, что все стрелки попадут.

A) 0,52

B) 0,38

C) 0,92

D) 0,12

Е) 0,05

$$$ 59 С

Три стрелка независимо друг от друга стреляют по целям вероятность попадания в цель для первого стрелка равна 0,6 для второго равна 0,5 для третьего 0,4. Какова вероятность, что попадет один стрелок.

A) 0,52

B) 0,92

C) 0,42

D) 0,12

Е) 0,05

$$$ 61 A

В одной урне 3 – белых и 5 – чёрных шаров, в другой 5 – белых и 2 – чёрных. С каждой урны взяли по шару. Какова вероятность того, что шары будут одного цвета?

A)25/56

В)15/56

C) 5/28

D) 8/15

E) 7/15

$$$ 63 С

В одной урне 3 – белых и 5 – чёрных шаров, в другой 5 – белых и 2 – чёрных. С каждой урны взяли по шару. Какова вероятность того, что шары будут черного цвета?

A)25/56

В)15/56

C) 5/28

D) 8/15

E) 7/15

$$$ 65 С

В одной урне 3 – белых и 5 – чёрных шаров, в другой 5 – белых и 2 – чёрных. С каждой урны взяли по шару. Какова вероятность того, среди них хотя бы один белый?

A)25/56

В)15/56

C) 23/28

D) 8/15

E) 7/15

$$$ 67 А

В одном ящике 10 деталей, из них 3 бракованных, во втором ящике 15 деталей, из них 5 бракованных. Из каждого ящика взяли по одной детали. Какова вероятность того, что обе бракованные?

A)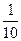

B)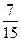

C)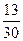

D)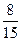

E)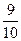

$$$ 69 С

В одном ящике 10 деталей, из них 3 бракованных, во втором ящике 15 деталей, из них 5 бракованных. Из каждого ящика взяли по одной детали. Какова вероятность того, что только одна бракованная?

A)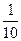

B)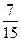

C)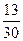

D)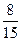

E)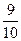

$$$ 71 Е

В одном ящике 10 деталей, из них 3 бракованных, во втором ящике 15 деталей, из них 5 бракованных. Из каждого ящика взяли по одной детали. Какова вероятность того, что хотя бы одна годная?

A)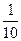

B)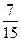

C)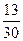

D)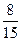

E)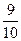

$$$ 73 A

В первой урне пять белых и три чёрных шаров, во второй три белых и два чёрных шаров. Из первой урны во вторую переложили один шар, а затем из второй урны вынули наугад один шар. Определить вероятность того, что вынутый шар белый?

A)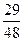

B)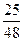

C)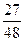

D)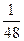

E) 2/5 .

$$$ 75 A

В первой урне 6 белых и 4 чёрных шаров, во второй 6 белых и 4 чёрных шаров. Из первой урны во вторую переложили один шар, а затем из второй урны вынули наугад один шар. Определить вероятность того, что вынутый шар белый?

A) 0,6

B) 0,5

C) 0,3

D) 0,4

E) 0,7

$$$ 77 D

Из урны, содержащей 3 белых и 2 черных шара переложен один шар в урну с 2 белыми и с 3 чёрными шарами, после чего из второй урны был вынут 1 шар какова вероятность того, что вынутый шар оказался белым?

A)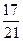

B)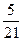

C)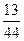

D)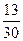

E)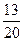

$$$ 79 В

Имеются три одинаковых по виду ящика. В первом ящике 20 белых шаров, во втором 10 белых и 10 чёрных шаров, в третьем 20 чёрных шаров. Из выбранного наугад ящика вынули шар. Найти вероятность того, что шар оказался белым.

A) 1

B) 1/2

C) 0,75

D) 1/3

E) 2/3.

$$$ 81 А

Имеются три одинаковых по виду ящика. В первом ящике 5 белых и 5 черных шаров, во втором 7 белых и 3 чёрных шаров, в третьем 2 белых и 8 чёрных шаров. Из выбранного наугад ящика вынули шар. Найти вероятность того, что шар оказался белым.

A)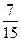

B )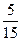

C)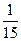

D)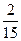

E)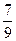

$$$ 83 В

Имеются три одинаковых по виду ящика. В первом ящике 5 белых шаров, во втором 5 белых и 5 чёрных шаров, в третьем 10 чёрных шаров. Из выбранного наугад ящика вынули шар. Найти вероятность того, что шар оказался белым.

A)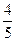

B )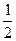

C)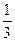

D)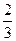

E)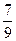

$$$ 85 D

В урну содержащую 2 шара положили 1 белый шар. Затем наудачу взяли 1 шар Найти вероятность что шар окажется белым, если равновозможны все предположения о первоначальном составе шаров.

A)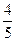

B )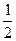

C)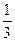

D)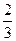

E)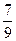

$$$ 87 В

В урну содержащую 2 шара положили 2 белых шара. Затем наудачу взяли 1 шар Найти вероятность что шар окажется белым, если равновозможны все предположения о первоначальном составе шаров.

A)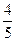

B )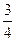

C)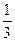

D)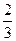

E)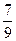

$$$ 89 А

В урну содержащую 2 шара положили 3 белых шара. Затем наудачу взяли 1 шар Найти вероятность что шар окажется белым, если равновозможны все предположения о первоначальном составе шаров.

A)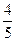

B )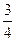

C)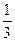

D)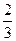

E)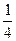

$$$ 91 А

В цехе первый автомат выпускает 20% всех деталей, второй 30%. Первый автомат допускает 3 % брака, второй 5% брака. Найти вероятность того, что наудачу взятая деталь бракованная?

A) 0,021

B ) 0,039

C) 0,041

D) 0,052

E) 0,014

$$$ 93 С

В цехе первый автомат выпускает 60% всех деталей, второй 40%. Первый автомат допускает 4 % брака, второй 5% брака. Найти вероятность того, что наудачу взятая деталь бракованная?

A) 0,021

B ) 0,039

C) 0,044

D) 0,052

E) 0,014

$$$ 95 А

Первый завод выпускает 1000 всех деталей, второй 2000, третий завод 3000. Первый завод выпускает 60 % первого сорта, второй 70% первого сорта, третий – 80 % первого сорта деталей. Найти вероятность того, что наудачу взятая деталь окажется первого сорта ?

A)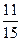

B )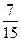

C)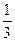

D)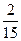

E)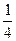

$$$ 97 А

В цехе первый автомат выпускает 20% всех деталей, второй 30%. Первый автомат допускает 3 % брака, второй 5% брака. Наудачу взятая деталь оказалась бракованной. Найти вероятность того, что она была изготовлена первым автоматом?

A)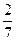

B )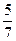

C)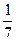

D)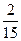

E)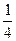

$$$ 99 Е

В цехе первый автомат выпускает 40% всех деталей, второй 60%. Первый автомат допускает 1 % брака, второй 2% брака. Наудачу взятая деталь оказалась бракованной. Найти вероятность того, что она была изготовлена первым автоматом?

A)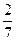

B )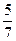

C)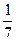

D)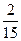

E)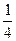

$$$ 101 С

В цехе первый автомат выпускает 60% всех деталей, второй 40%. Первый автомат допускает 4 % брака, второй 5% брака. Наудачу взятая деталь оказалась бракованной. Найти вероятность того, что она была изготовлена первым автоматом?

A)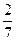

B )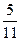

C)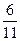

D)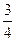

E)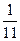

$$$ 103 В

Первый завод выпускает 2000 всех деталей, второй 5000, третий завод 3000. Первый завод выпускает 40 % первого сорта, второй 20% первого сорта, третий – 10 % первого сорта деталей. Наудачу взятая деталь оказалась первого сорта. Найти вероятность того, что она была изготовлена первым заводом

A)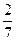

B )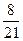

C)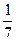

D)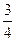

E)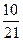

$$$ 105 С

Первый завод выпускает 2000 всех деталей, второй 5000, третий завод 3000. Первый завод выпускает 40 % первого сорта, второй 20% первого сорта, третий – 10 % первого сорта деталей. Наудачу взятая деталь оказалась первого сорта. Найти вероятность того, что она была изготовлена третьим заводом.

A)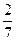

B )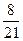

C)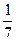

D)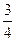

E)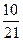

$$$ 107 А

Первый завод выпускает 1000 всех деталей, второй 2000, третий завод 3000. Первый завод выпускает 60 % первого сорта, второй 70% первого сорта, третий – 80 % первого сорта деталей. Наудачу взятая деталь оказалась первого сорта. Найти вероятность того, что она была изготовлена первым заводом.

A)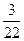

B )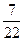

C)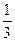

D)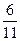

E)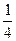

$$$ 109 Е

Найти вероятность того, что при бросании монеты 2 раза герб появится только 1 раз

А) 3\4

В) 2\3

С) 1\4

Д) 1

Е) 1\2

$$$ 111 С

Найти вероятность того, что при бросании монеты 2 раза герб ни разу не появится.

А) 3\4

В) 2\3

С) 1\4

Д) 1

Е) 1\2

$$$ 113 Д

Найти вероятность того, что при бросании трех монет герб появится только один раз

А) 1\8

В) 5\8

С) 7\8

Д) 3\8

Е) 1

$$$ 115 С

Найти вероятность того, что при бросании трех монет герб появится два раза.

А) 7\8

В) 1\8

С) 3\8

Д) 5\8

Е) 0

$$$ 117 D

Найти вероятность того, что при подбрасывании 4 монет хотя бы на одной из них выпадает герб.

A)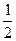

B)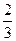

C)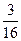

D)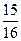

E)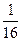

$$$ 119 А

Найти вероятность того, что при подбрасывании 4 монет герб выпадает только 2 раза.

A)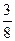

B)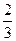

C)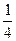

D)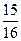

E)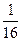

$$$ 121 Е

Найти вероятность того, что при подбрасывании 4 монет герб выпадает на всех монетах.

A)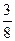

B)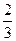

C)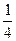

D)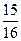

E)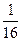

$$$ 123 С

Найти вероятность того, что бросании монеты 4 раза герб выпадает более двух раз.

A)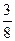

B)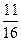

C)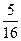

D)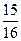

E)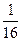

$$$ 125 В

Найти вероятность того, что бросании монеты 4 раза герб выпадает не менее двух раз.

A)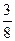

B)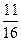

C)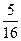

D)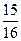

E)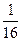

$$$ 127 А

Найти вероятность того, что при бросании монеты 5 раз хотя бы один раз появится герб

А)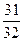

В)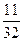

С) 1

D)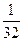

Е)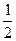

$$$ 129 D

Найти вероятность того, что при бросании монеты 5 раз только три раза появится герб

А)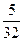

В)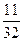

С) 1

D)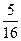

Е)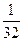

$$$ 131 С

Найти вероятность того, что при бросании монеты 5 раз герб появится менее 3 раз.

А)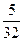

В)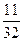

С)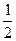

D)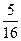

Е)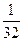

$$$ 133 А

Найти вероятность того, что при бросании монеты 5 раз герб появится не более 3 раз.

А)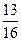

В)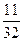

С)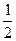

D)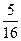

Е)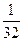

$$$ 135 В

Монету подбрасывают 6 раз. Какова вероятность того, что 4 раза она падает гербом вверх.

А)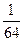

В)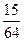

С)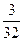

D)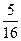

Е)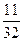

$$$ 137 С

Монету подбрасывают 6 раз. Какова вероятность того, что 1 раз она упадет гербом вверх.

А)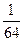

В)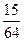

С)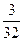

D)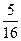

Е)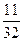

$$$ 139 Е

Монету подбрасывают 6 раз. Какова вероятность того, герб появится не менее 4 раз.

А)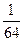

В)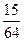

С)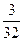

D)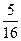

Е)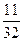

$$$ 141 Е

Монету подбрасывают 6 раз. Какова вероятность того, герб появится не более 2 раз.

А)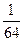

В)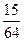

С)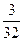

D)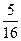

Е)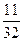

$$$ 143 Е

Найти вероятность того, что при бросании игральной кости 3 раза хотя бы один раз появится 5 очков.

А)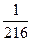

В) 0

С)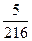

D)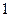

Е)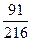

$$$ 145 А

Найти вероятность того, что при бросании игральной кости 3 раза 5 очков выпадет ровно 3 раза.

А)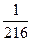

В)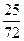

С)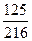

D)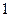

Е)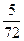

$$$ 147 С

Найти вероятность того, что при бросании игральной кости 3 раза 5 очков не выпадет ни разу.

А)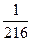

В)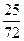

С)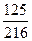

D)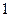

Е)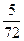

$$$ 149 А

Вероятность попадания стрелком при одном выстреле 0.8. Найти вероятность того, что при трех выстрелах стрелок попадет все три раза.

А) 0,512

В) 0,124

С) 0,228

D) 0,384

Е) 0,5

$$$ 151 Е

Вероятность попадания стрелком при одном выстреле 0.8. Найти вероятность того, что при трех выстрелах стрелок попадет хотя бы один раз.

А) 0,324

В) 0,124

С) 0,228

D) 0,384

Е) 0,992

$$$ 153 D

Вероятность попадания стрелком при одном выстреле 0.8. Найти вероятность того, что при трех выстрелах стрелок попадет не менее 2 раз.

А) 0,104

В) 0,124

С) 0,228

D) 0,896

Е) 0,5

$$$ 155 С

Вероятность попадания стрелком при одном выстреле 0.8. Найти вероятность того, что при трех выстрелах стрелок попадет не более 2 раз.

А) 0,104

В) 0,124

С) 0,488

D) 0,896

Е) 0,5

$$$ 157 D

В партии деталей 10% бракованных. Найти вероятность того, что среди трех отобранных хотя бы одна бракованная.

А) 0,729

В) 0,027

С) 0,001

D) 0,271

Е) 0,243

$$$ 159 А

В партии деталей 10% бракованных. Найти вероятность того, что среди трех отобранных ни одной бракованной.

А) 0,729

В) 0,027

С) 0,001

D) 0,384

Е) 0,243

$$$ 161 Е

При выработке некоторой массовой продукции вероятность появления одного нестандартного изделия составляет 0.01. Какова вероятность того, что в партии 100 изделий этой продукции 2 изделия будет нестандартными.

А) 0.368

В) 0.96

С) 0.061

D) 0.162

Е) 0.184

$$$ 163 С

При выработке некоторой массовой продукции вероятность появления одного нестандартного изделия составляет 0.01. Какова вероятность того, что в партии 100 изделий этой продукции 3 изделия будет нестандартными.

А) 0.368

В) 0.96

С) 0.061

D) 0.162

Е) 0.184

$$$ 165 В

При выработке некоторой массовой продукции вероятность появления одного нестандартного изделия составляет 0.01. Какова вероятность того, что в партии 100 изделий этой продукции менее 3 изделий будет нестандартными.

А) 0.368

В) 0.92

С) 0.06

D) 0.16

Е) 0.18

$$$ 167 Е

При выработке некоторой массовой продукции вероятность появления одного нестандартного изделия составляет 0.01. Какова вероятность того, что в партии 100 изделий этой продукции не более 3 изделий будет нестандартными.

А) 0.368

В) 0.967

С) 0.061

D) 0.162

Е) 0.981

$$$ 169 В

С базы в магазин отправлено 4000 тщательно упакованных доброкачественных изделий. Вероятность того, что изделие повредится в пути равно 0.0005. Найти вероятность того, что в магазин прибудут 2 испорченных изделия

A) 0.13

В) 0.27

С) 0.18

D) 0.98

E) 0,77

$$$ 171 А

С базы в магазин отправлено 4000 тщательно упакованных доброкачественных изделий. Вероятность того, что изделие повредится в пути равно 0.0005. Найти вероятность того, что в магазин прибудут все изделия неповрежденными.

A) 0.135

В) 0.276

С) 0.183

D) 0.98

E) 0,774

$$$ 173 Е

С базы в магазин отправлено 4000 тщательно упакованных доброкачественных изделий. Вероятность того, что изделие повредится в пути равно 0.0005. Найти вероятность того, что в магазин прибудет хотя бы одно испорченное изделие.

A) 0.135

В) 0.273

С) 0.184

D) 0.982

E) 0,865

$$$ 175 Е

С базы в магазин отправлено 4000 тщательно упакованных доброкачественных изделий. Вероятность того, что изделие повредится в пути равно 0.0005. Найти вероятность того, что в магазин прибудут более 2- х испорченных изделия

A) 0.135

В) 0.273

С) 0.675

D) 0.982

E) 0,325

$$$ 177 С

С базы в магазин отправлено 4000 тщательно упакованных доброкачественных изделий. Вероятность того, что изделие повредится в пути равно 0.0005. Найти вероятность того, что в магазин прибудут не более 3- х испорченных изделия

A) 0.135

В) 0.273

С) 0.855

D) 0.982

E) 0,774

$$$ 179 С

Вероятность выигрыша на один билет лотереи 0.02. Какова вероятность того, что из 150 билетов выигрыш выпадет на 2 билета.

A) 0.049

B) 0.149

C) 0.224

D) 0.275

E) 0.336

$$$ 181 А

Вероятность выигрыша на один билет лотереи 0.02. Какова вероятность того, что из 150 билетов выигрыша не будет.

A) 0.049

B) 0.149

C) 0.224

D) 0.275

E) 0.336

$$$ 182 Е

Вероятность выигрыша на один билет лотереи 0.02. Какова вероятность того, что из 150 билетов выигрыш выпадет хотя бы на 1 билет.

A) 0.049

B) 0.149

C) 0.224

D) 0.275

E) 0.951

$$$ 184 Е

Вероятность выигрыша на один билет лотереи 0.02. Какова вероятность того, что из 150 билетов выигрышных будет более двух.

A) 0.198

B) 0.149

C) 0.224

D) 0.275

E) 0.578

$$$ 185 А

Вероятность выигрыша на один билет лотереи 0.02. Какова вероятность того, что из 150 билетов выигрышных будет не менее трех.

A) 0.578

B) 0.149

C) 0.224

D) 0.275

E) 0.951

$$$ 187 С

Вероятность выигрыша на один билет лотереи 0.02. Какова вероятность того, что из 100 билетов выигрыш выпадет хотя бы на один билет

A)0.34

B) 0.76

C) 0.86

D) 0.43

E) 0.562

$$$ 189 А

Завод отправил на базу 500 изделий. Вероятность повреждения в пути 0.002. Найти вероятность того, что. в пути будет повреждено ровно 3 изделия.

А) 0.062

В) 0.0428

С) 0.0225

D) 0.12

Е) 0.087

$$$ 191 С

Стрелок выполнил 400 выстрелов, вероятность одного попадания 0,8. Найти вероятность того, что он попадет ровно 310 раз.

А) 0.041

В) 0.042

С) 0.023

D) 0.012

Е) 0.087

$$$ 193 Е

Стрелок выполнил 400 выстрелов, вероятность одного попадания 0,8. Найти вероятность того, что он попадет ровно 305 раз.

А) 0.041

В) 0.042

С) 0.007

D) 0.002

Е) 0.009

$$$ 195 В

Стрелок выполнил 400 выстрелов, вероятность одного попадания 0,8. Найти вероятность того, что он попадет от 320 до 330 раз.

А) 0.630

В) 0.394

С) 0.226

D) 0.129

Е) 0.877

$$$ 197 D

Стрелок выполнил 400 выстрелов, вероятность одного попадания 0,8. Найти вероятность того, что он попадет от 330 до 350 раз.

А) 0.630

В) 0.394

С) 0.226

D) 0.105

Е) 0.494

$$$ 199 С

Всхожесть семян, хранящегося на складе, равна 70%. Какова вероятность того, что среди 100 зерен число всхожих составит 80 штук.

А) 0.630

В) 0.004

С) 0.008

D) 0.005

Е) 0.494

$$$ 201 А

Всхожесть семян, хранящегося на складе, равна 70%. Какова вероятность того, что среди 100 зерен число всхожих составит 75 штук.

А) 0.048

В) 0.004

С) 0.008

D) 0.005

Е) 0.094

$$$ 203 D

Всхожесть семян, хранящегося на складе, равна 80%. Какова вероятность того, что среди 100 зерен число всхожих составит от 68 до 90 штук.

А) 0.630

В) 0.394

С) 0.729

D) 0.666

Е) 0.004

$$$ 205 D

Всхожесть семян, хранящегося на складе, равна 80%. Какова вероятность того, что среди 100 зерен число всхожих составит от 70 до 80 штук.

А) 0.630

В) 0.394

С) 0.729

D) 0.485

Е) 0.004

$$$ 207 А

В партии деталей 30 % бракованных. Найти математическое ожидание случайной величины Х – числа бракованных деталей среди 200 отобранных.

А) 60

В) 42

С) 6,48

D) 6

Е) 5,76

$$$ 209 С

В партии деталей 30 % бракованных. Найти среднее квадратическое отклонение случайной величины Х – числа бракованных деталей среди 200 отобранных.

А) 60

В) 42

С) 6,48

D) 6

Е) 5,76

$$$ 211 D

В партии деталей 20 % бракованных. Найти дисперсию случайной величины Х – числа бракованных деталей среди 200 отобранных.

А) 60

В) 40

С) 6,48

D) 32

Е) 5,76

$$$ 213 D

Вероятность попадания в мишень 0,6. Найти математическое ожидание величины Х – числа попаданий при 300 выстрелах.

А) 72

В) 40

С) 8,48

D) 180

Е) 5,76

$$$ 215 С

Вероятность попадания в мишень 0,6. Найти среднее квадратическое отклонение величины Х – числа попаданий при 300 выстрелах.

А) 72

В) 40

С) 8,48

D) 180

Е) 5,76

$$$ 217 С

Всхожесть семян, хранящегося на складе, равна 90%. Найти дисперсию случайной величины Х – числа всхожих семян среди 1000.

А) 100

В) 9,49

С) 90

D) 900

Е) 950

$$$ 219 С

Вероятность попадания в мишень 0,6. Было произведено 40 выстрелов. Найти наивероятнейшее число попаданий.

А) 72

В) 40

С) 24

D) 18

Е) 20

$$$ 221 А

Вероятность попадания в мишень 0,8. Было произведено 89 выстрелов. Найти наивероятнейшее число попаданий.

А) 71,72

В) 71

С) 72

D) 78

Е) 62

$$$ 223 Е

В партии деталей 30% бракованных. Найти наивероятнейшее число бракованных деталей среди 145 отобранных.

А) 42

В) 43,44

С) 24

D) 44

Е) 43

$$$ 225 D

В автопарке 70 машин. Вероятность поломки машины 0,2. Найти наивероятнейшее число исправных машин.

А) 54

В) 55

С) 55,56

D) 56

Е) 52

$$$ 227 А

В автопарке 79 машин. Вероятность поломки машины 0,3. Найти наивероятнейшее число исправных машин.

А) 55, 56

В) 55

С) 56

D) 57

Е) 58

$$$ 229 А

В автопарке 6 машин. Вероятность поломки машины 0,5. Найти наивероятнейшее число исправных машин и ее вероятность.

А)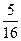

В)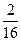

С)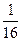

D)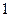

Е)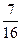

$$$ 231 В

Вероятность что деталь будет первого сорта 0,7. Найти наивероятнейшее число деталей первого сорта среди 3 деталей и ее вероятность.

А) 0,323

В) 0,441

С) 0,409

D) 0,087

Е) 0,663

$$$ 233 D

Вероятность что деталь будет стандартной 0,9. Найти наивероятнейшее число деталей первого сорта среди 3 деталей и ее вероятность.

А) 0,323

В) 0,441

С) 0,409

D) 0,729

Е) 0,663

$$$ 235 А

Вероятность что деталь будет стандартной 0,5. Найти наивероятнейшее число деталей первого сорта среди 6 деталей и ее вероятность.

А)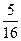

В)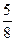

С)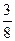

D)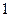

Е)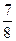

$$$ 237 С

Вероятность попадания в мишень 0,5. Найти наивероятнейшее число попаданий при 4 выстрелах и ее вероятность.

А)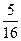

В)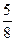

С)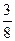

D)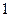

Е)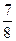

$$$ 239 Е

Вероятность заболеть гриппом 10 %. Найти наивероятнейшее число заболевших гриппом среди 200 людей ее вероятность.

А) 0,133

В) 0,041

С) 0,009

D) 0,046

Е) 0,095

@@@ 3. Случайные величины

$$$ 1 В

Случайная величина Х задана законом распределения. Найти М(Х²)

Х
Р	0.1	0.4	0.3	0.2

А) 43.6

В) 45.8

С) 48.4

D) 52.1

Е) 54

$$$

$$$ 3 А

Дано М(Х)=4, М(У)=2. Найти М(4Х+У.)

А) 18

В) 57

С) 33

D) 9

Е) 8

$$$ 5 Е

Дано М(Х)=6, М(У)=3. Найти М(Х+2У.)

А) 21

В) 57

С) 33

D) 9

Е) 12

$$$ 7 В

Известно, что Д(Х)=5, Д(У)=3. Найти Д(3Х-2У).

А) 9

В) 57

С) 33

D) 21

Е) 53

$$$ 9 Е

Известно, что Д(Х)=3, Д(У)=4. Найти Д(Х-3У).

А) 9

В) 15

С) 33

D) 21

Е) 39

$$$ 11 В

Известно, что Д(Х)=10, Д(У)=2. Найти Д(3Х-2У).

А) 34

В) 98

С) 82

D) 80

Е) 53

$$$ 13 С

Известно, что Д(Х)=20. Найти Д(2Х+3).

А) 83

В) 28

С) 80

D) 80

Е) 43

$$$ 15 А

Известно, что М(Х)=7. Найти М(3-Х).

А) -4

В) 10

С) 7

D) -7

Е) 9