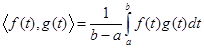Переход от векторного пространства к пространству функций

О Т Ч Е Т

ПРАКТИЧЕСКАЯ РАБОТА №9

ДИСЦИПЛИНА:	" Функциональная логика и теория алгоритмов "
ТЕМА:	" Дискретное преобразование Фурье"

Выполнил: студент гр. РПД.Б-32	Жучкова А.Д._______________
Проверил:	Соловьёв И.В.______________

Дата сдачи (защиты) упражнения:
Результаты сдачи (защиты): Количество рейтинговых баллов
Оценка

Калуга, 2014 г.

Цель работы: получить первичное представление о дискретном преобразовании Фурье.

Задание: изучить теоретические сведения, выполнить все задания упражнения и продемонстрировать преподавателю, оформить результаты выполнения в виде отчёта.

Теоретические сведения.

Физические параметры объектов реального мира обычно изменяются непрерывно, например, изменение температуры атмосферы от времени:

Так как температура изменяется непрерывно, теоретически можно проводить измерения через бесконечно малые промежутки времени. Однако при этом очень сильно будет тратиться память компьютера. Время, затрачиваемое на измерения, тоже будет велико. Стоит задуматься, насколько подобные измерения необходимы? Значение температуры не может резко измениться в течение секунды или даже минуты. Количество измерений можно резко сократить, проводя их через более длительные интервалы.

Сигнал, отражающий непрерывно изменяющуюся величину называется аналоговым. Сигнал, имеющий конечное число значений называется дискретным. Превратить аналоговый сигнал в дискретный можно с использованием выборки. Например, непрерывный сигнал температуры преобразуем в дискретный сигнал, выборкой значений через равные интервалы времени (измерение температуры один раз в минуту):

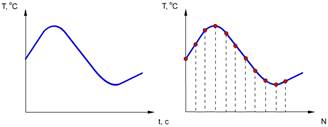
Подобные интервалы времени называются интервалы дискретизации. Если сигнал (функцию f) сделать дискретным и перевести в цифровую форму, то можно записать его в виде ряда значений из N точек.

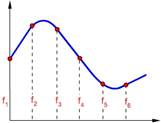
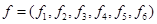
Другими словами непрерывную функцию можно представить в виде N-мерного вектора. Чем больше частота дискретизации, тем больше N и тем точнее вектор будет описывать изначальную функцию.

Если представить себе N-мерное пространство бесконечно большой размерности, то вектор функции f(t) будет соответствовать одной точке этого пространства. Это даёт возможность несколько по-другому взглянуть на процесс сравнения двух различных функций. В векторном пространстве существует понятие расстояния между двумя векторами и скалярное произведение. Для пространства функций эти понятия также могут быть использованы. Сделаем небольшой экскурс в геометрию.

Операции над векторами.

В двумерном пространстве даны два вектора 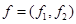и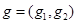

Норма вектора: 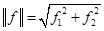или абсолютное значение.

Расстояние между векторами можно определить по формуле:

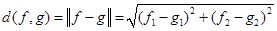
Расстояние – это один из параметров, определяющий силу связи между двумя векторами. Чем меньше расстояние, тем ближе векторы друг к другу. Вторым параметром, определяющим силу связи векторов, является скалярное произведение. Оно отражает угол между векторами:

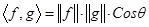
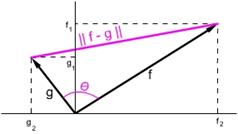
Через компоненты вектора скалярное произведение выражается:

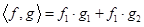Векторы взаимно перпендикулярны, если их скалярное произведение равно 0.

Ортонормированные базисы.

Для представления одномерных величин достаточно одного параметра. К примеру, для измерения длины используют один стандарт величины. Единица измерения - один миллиметр. 7 мм больше 1 мм в 7 раз, и содержит 7 единиц. В векторном пространстве также принято выбирать единицу измерения. В двумерном пространстве пара взаимно перпендикулярных векторов 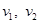называется ортогональным базисом. Если абсолютные значения этих векторов равны единице 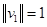, , 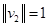то эта пара векторов является ортонормированным базисом. Например, выразим вектор f через векторы ортонормированного базиса:

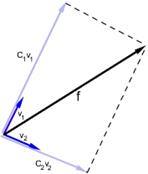
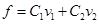
Любой вектор на плоскости можно выразить подобным образом, отличие будет заключаться лишь в значениях коэффициентов C₁ и C₂. Данные коэффициенты можно найти, используя скалярное произведение f и каждого из векторов базиса:

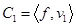
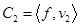
Переход от векторного пространства к пространству функций.

Скалярное произведение и расстояние между двумя векторами в двумерном пространстве мы определили. Для трёхмерного пространства норма вектора 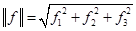. Если обобщить для N-мерного пространства получим:

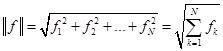
Если N будет стремиться к бесконечности, то получим:

вектор → функция сумма → интеграл

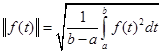
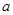- нижняя граница интервала, на котором определена функция, 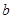- верхняя. Множитель 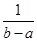введён для того чтобы ограничить значения нормы.

Таким образом, сделав переход от пространства векторов к пространству функций, можем получить следующее.

Скалярное произведение двух функций: