Для иллюстрации воспользуемся кругами Эйлера

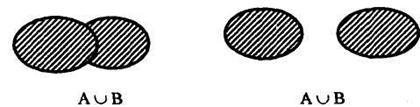
Объединение множеств А и В

Аналогично определяется объединение нескольких множеств. Пример 1.10.

а) Пусть А = {4, 5, 6}, В ={2,4, 6}.

Тогда А 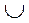B ={2,4, 5,6}.

б) Пусть А - множество чисел, которые делятся на 2, а В - множество чисел, которые делятся на 3:

A = {2,4,6,...}, B={3,6,9,...}.

Тогда A 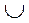B множество чисел, которые делятся на 2 или на 3:

АВ= {2, 3,4, 6, 8, 9,10,...}.

Разностью множества А и В называется множество А \ В, все элементы которого являются элементами множества А, но не являются элементами множества В:

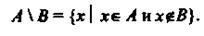
В отличие от двух предыдущих операций разность, во-первых, строго двухместна (т.е. только для 2-х множеств), а во-вторых, некоммутативная, т.е.:

Х\Y = Y\X. Для иллюстрации воспользуемся кругами Эйлера.

Разность множеств А и В

Пример 1.11.

а) A = {4, 5, 6}, В ={2,4, 6}.

А\В = {4,5}, В\А= {2}.

6) X={a,b,d},Y={b,d,e,h}.

X\Y={a} .

Y\X=\e,h}.

Симметрической равностью множеств А и В называется множество А + В:

A+B = (A\B) (B\A).

Для иллюстрации воспользуемся кругами Эйлера (рисунок 1.4).

Симметрическая разность множеств А и В

Пример 1.12.

а) A = {4,5,6},B={2,4,6}.

А\В={4,5},В\А= {2}, А+В = {2,4,5}.

б)Х={а, b, d), Y={b, d, e, h},X+ У= {а, е, h).

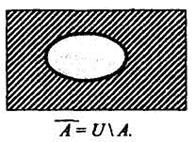
Для универсального множества U может быть определена операция дополнения.

Дополнением множества А называется множество А всех тех элементов х U, которые не принадлежат множеству A: A=U\A.

Для иллюстрации воспользуемся кругами Эйлера

Дополнение множества А

Пример 1.13.

Пусть А - множество положительных четных чисел. Тогда U - множество всех натуральных чисел и А - множество положительных нечетных чисел.

Алгебра множеств. Основные тождества алгебры множеств

Множества вместе с определенными на них операциями образуют алгебру множеств. Последовательность выполнения операций задается с помощью формул алгебры множеств. Например,

А (В С), (А \ В) + С - формулы алгебры множеств.

1. Коммутативность - переместительный закон.

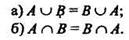
2. Ассоциативность - сочетательный закон

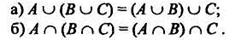
3. Дистрибутивность — распределительный закон,

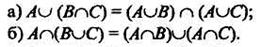
4. Закон де Моргана. Свойство дополнительных множеств.

а) 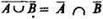(дополнение к объединению есть пересечение дополнений);

б) 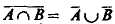(дополнение к пересечению есть объединение дополнений).

5. Идемпотентность.

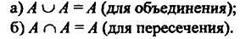
6. Поглощение.

Всякое бесконечное подмножество счетного множества счетно.

Пример 1.19.

Множество А = {3, 6, ..., 3n, ...} счетно, т.к. А - бесконечное подмножество множества натуральных чисел, А N.

Объединение конечной или счетной совокупности счетных множеств счетно.

Пример 1.20.

Множество А = {О, 1, ..., n,...} неотрицательных целых чисел счетно, множество В = {0, —1, ..., -n, ...} неположительных целых чисел тоже счетно, поэтому множество всех целых чисел

С = A B ={..., -n,...- 2, -1,0,1,2,..., п, ...} тоже счетно.

Множество всех рациональных чисел, т.е. чисел вида p/q, где р и q целые числа, счетно.

Если А = {а₁ а₂, ...} и В = {b₁ b₂,...} - счетные множества, то множество всех пар С = {(a_k, b_п), k=1,2,...; n = 1,2,...} счетно.

Пример 1.21.

Геометрический смысл пары (а_k Ь_п) - точка на плоскости с рациональными координатами (q_k, b_n). Поэтому можно утверждать, что множество всех точек плоскости с рациональными координатами счетно.