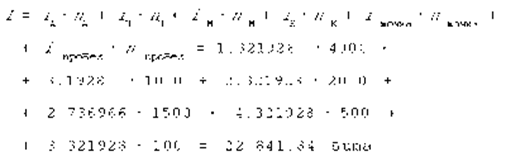Приближение разной вероятности встречаемости символов в тексте

В этом приближении учитывается, что в реальном тексте разные символы встречаются с разной частотой. Отсюда следует, что вероятности появления разных символов в определенной позиции текста различны и, следовательно, различаются их информационные веса.

Статистический анализ русских текстов показывает, что частота появления буквы “о” составляет 0,09. Это значит, что на каждые 100 символов буква “о” в среднем встречается 9 раз. Это же число обозначает вероятность появления буквы “о” в определенной позиции текста: po = 0,09.Отсюда следует, что информационный вес буквы “о” в русском тексте равен:

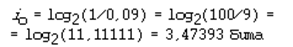
Самой редкой в текстах буквой является буква “ф”. Ее частота равна 0,002. Отсюда:

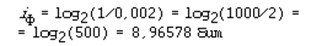
Отсюда следует качественный вывод: информационный вес редких букв больше, чем вес часто встречающихся букв.

Как же вычислить информационный объем текста с учетом разных информационных весов символов алфавита? Делается это по следующей формуле:

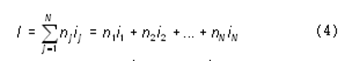
Здесь N – размер (мощность) алфавита; n_j – число повторений символа номер j в тексте; i_j – информационный вес символа номер j.

Пример 1. Для записи текста используются только строчные буквы русского алфавита и “пробел” для разделения слов. Какой информационный объем имеет текст, состоящий из 2000 символов (одна печатная страница)?

Решение. В русском алфавите 33 буквы. Сократив его на две буквы (например, “ё” и “й”) и введя символ пробела, получаем очень удобное число символов – 32. Используя приближение равной вероятности символов, запишем формулу Хартли:

2ⁱ =32 = 2⁵

Отсюда: i = 5 бит – информационный вес каждого символа русского алфавита. Тогда информационный объем всего текста равен:

I = 2000 · 5 = 10 000бит

Пример 2. Вычислить информационный объем текста размером в 2000 символов, в записи которого использован алфавит компьютерного представления текстов мощностью 256.

Решение. В данном алфавите информационный вес каждого символа равен 1 байту (8 бит). Следовательно, информационный объем текста равен 2000 байт.

В практических заданиях по данной теме важно отрабатывать навыки учеников в пересчете количества информации в разные единицы: биты – байты – килобайты – мегабайты – гигабайты. Если пересчитать информационный объем текста из примера 2 в килобайты, то получим:

2000 байт = 2000/1024 1,9531 Кб

Пример 3. Объем сообщения, содержащего 2048 символов, составил 1/512 часть мегабайта. Каков размер алфавита, с помощью которого записано сообщение?

Решение. Переведем информационный объем сообщения из мегабайтов в биты. Для этого данную величину умножим дважды на 1024 (получим байты) и один раз – на 8:

I = 1/512 · 1024 · 1024 · 8 = 16 384 бита.

Поскольку такой объем информации несут 1024 символа (К), то на один символ приходится:

i = I/K = 16 384/1024 = 16 бит.

Отсюда следует, что размер (мощность) использованного алфавита равен 2¹⁶ = 65 536 символов.

Пример 4. В алфавите племени МУМУ всего 4 буквы (А, У, М, К), один знак препинания (точка) и для разделения слов используется пробел. Подсчитали, что в популярном романе “Мумука” содержится всего 10 000 знаков, из них: букв А – 4000, букв У – 1000, букв М – 2000, букв К – 1500, точек – 500, пробелов – 1000. Какой объем информации содержит книга?

Решение.Поскольку объем книги достаточно большой, то можно допустить, что вычисленная по ней частота встречаемости в тексте каждого из символов алфавита характерна для любого текста на языке МУМУ. Подсчитаем частоту встречаемости каждого символа во всем тексте книги (т.е. вероятность) и информационные веса символов

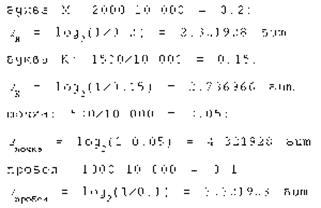
Общий объем информации в книге вычислим как сумму произведений информационного веса каждого символа на число повторений этого символа в книге: