Глава 13
Декомпозиция задач и графы AND/OR
В этой главе...
13.1. Представление задач в виде графов AND/OR 277
13.2. Примеры представлений в виде графа AND/OR 281
13.3. Основные процедуры поиска в графе AND/OR 284
13.4. Поиск в графе AND/OR по заданному критерию 289
Графы AND/OR могут служить удобным средством представления тех задач, которые возможно естественным образом разложить на ряд взаимно независимых подзадач. К примерам таких задач относится поиск маршрута, проектирование, символическое интегрирование, игры, доказательство теорем и т.д. В этой главе рассматриваются программы для поиска в графах AND/OR, включая поиск по заданному критерию в графе AND/OR, управляемый эвристическими средствами.
13.1. Представление задач в виде графов AND/OR
В главах 11 и 12 в основном рассматривались способы решения задач, представленных с помощью пространства состояний. В соответствии с этим решение задачи сводилось к поиску пути в графе пространства состояний. Но для некоторых категорий задач более естественно подходит другое представление, в виде графа AND/OR. В основе такого представления лежит декомпозиция задачи на подзадачи. Декомпозиция на подзадачи может применяться, если подзадачи являются взаимно независимыми и поэтому могут решаться независимо друг от друга.
Проиллюстрируем сказанное выше на примере. Рассмотрим задачу поиска маршрута между двумя указанными городами на дорожной карте, показанной на рис. 13.1. На данный момент значения длины маршрутов будут игнорироваться. Эту задачу, безусловно, можно сформулировать как поиск пути в пространстве состояний, Соответствующее пространство состояний может выглядеть полностью аналогично этой карте: узлы в пространстве состояний соответствуют городам, дуги — прямым соединениям между городами, а стоимости дуг — расстояниям между городами. Но может рассматриваться и другое представление этой задачи, основанное на ее естественной декомпозиции.
На карте, приведенной на рис. 13.1, имеется также река. Предположим, что эту реку можно пересечь только с помощью двух мостов, один из которых находится в городе f, а другой - в городе д. Очевидно, что необходимо включить в разрабатываемый маршрут один из мостов, поэтому маршрут должен пройти или через f, или через д. Таким образом, имеются два описанных ниже основных варианта.
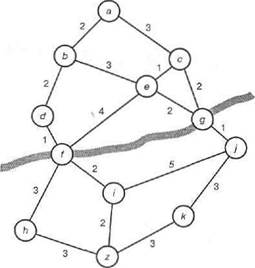 |
Рис. 13.1. Поиск маршрута между городами а и z по дорожной карте. Реку можно пересечь е пункте f или д. Представление этой задачи в виде графа AND/OR показано на рис. 13.2
Чтобы найти путь от а до z, необходимо выполнить одно из следующих действий.
1. Найти путь от а до г через f,
2. Найти путь от а до z через д.
Теперь каждый из этих двух вариантов задачи можно разложить на подзадачи, как описано ниже.
1. Чтобы найти путь от а до z через f, необходимо выполнить следующее:
1.1. найти путь от а до f;
1.2. найти путь от f до г.
2. Чтобы найти путь от а до z через д, необходимо выполнить следующее:
2.1. найти путь от а до д;
2.2. найти путь от д до z.
В конечном итоге имеются два основных варианта решения первоначальной задачи: проложить маршрут через f или проложить его через д. Кроме того, каждый из этих вариантов задачи можно разделить на две подзадачи {соответственно, 1.1 и 1.2 или 2.1 и 2.2). Здесь важно то, что (в обоих вариантах) каждая из подзадач может быть решена независимо от другой. Такую декомпозицию можно представить в виде графа AND/ОН (рис. 13.2). Обратите внимание на две дуги, соединенные кривой линией, которые обозначают связь AND между подзадачами. Безусловно, что граф, показанный на рис. 13.2, представляет собой только верхнюю часть соответствующего дерева AND/OR. Дальнейшая декомпозиция подзадач может быть основана на рассмотрении других промежуточных городов.
Какими являются целевые узлы в подобном графе AND/OR? Целевые узлы соответствуют подзадачам, которые являются тривиальными, или "простейшими". В данном примере такой подзадачей будет "поиск маршрута от а до с", поскольку на дорожной карте имеется прямое соединение между городами а и с.
В этом примере введены некоторые важные понятия. Граф AND/OR представляет собой ориентированный граф, узлы которого соответствуют задачам, а дуги обозна-
Часть II. Применение языка Prolog в области искусственного интеллекта
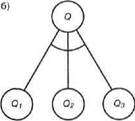
чают отношения между задачами. Имеются также отношения между самими дугами. Этими отношениями являются AND и OR, в зависимости от того, требуется ли решить только одну из задач-преемников или сразу несколько (рис. 13.3). Б принципе, из любого узла могут исходить и дуги, связанные отношением AND, и дуги, связанные отношением OR. Но мы предполагаем, что каждый узел имеет либо только преемников AND, либо только преемников OR. Дело в том, что каждый граф AND/OR можно преобразовать в стандартную форму, введя по мере необходимости вспомогательные узлы OR. Поэтому узел, из которого исходят только дуги AND, называется узлом AND, а узел, из которого исходят только дуги OR, называется узлом OR.
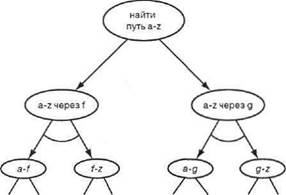 |
Рис. 13.2. Представление задачи поиска маршрута, приведенной на рис 13.1. е виде графа AND/OR. Узлы соответствуют задачам или подзадачам, а дуги, соединенные кривыми, показывают, что должны быть решены все (в данном случае обе) подзадачи
 |
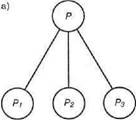 |
Рис. 13.3. Два типа узлов в графе AND/OR: а) чтобы решить задачу Р, достаточно решить любую us подзадач Pi, P2 или ...; б) чтобы решить задачу Q, необходимо решить все подзадачи, и Q1. и 02. и ...
В представлении в виде пространства состояний решение задачи сводилось к поиску пути в пространстве состояний. Каково же решение в представлении в виде графа AND/OR? Безусловно, что любое решение должно включить все подзадачи любого узла AND. Поэтому теперь решение является не путем, а деревом. Такое дерево решения, Т, определяется следующим образом.
• Первоначальная проблема, Р, является корневым узлом дерева Г.
• Если Р — узел OR, то в дереве Т находится один и только один из его преемников (по графу AND/OR) вместе с его собственным деревом решения.
• Если Р — узел AND, то в дереве т находятся все его преемники (по графу AND/OR) наряду с их деревьями решения,
Глава 13, Декомпозиция задач и графы AND/OR
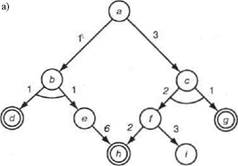
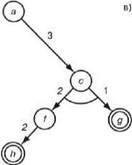
Это определение показано на рис. 13.4. На данном рисунке показаны также стоимости, назначенные дугам. Стоимости позволяют сформулировать критерий оптимизации. Можно, например, определить стоимость графа решения как сумму всех стоимостей дуг в этом графе. Поскольку нас обычно интересует минимальная стоимость, то предпочтительным является граф решения, показанный на рис. 13.4,в.
 |
 |
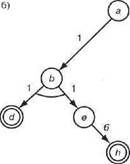 |
Рис. 13.4. Примеры графов решения: а) граф AND/OR, в котором d, g и h являются целевыми узлами, а — задача, которая должна быть решена; б) и в) два дерева решения, стоимость которых составляет соответственна 9 и 8. Здесь стоимость дерева решения определена как сумма всех стоимостей дуг в дереве решения
■Но мы не обязаны всегда рассматривать стоимости дуг в качестве критерия оптимизации. Иногда более естественно связать стоимости с узлами, а не с дугами или связать их и с дугами, и с узлами.
На основании сказанного выше можно сделать следующие выводы.
• Представление задачи в виде графа AND/OR основано на принципе декомпозиции задачи на подзадачи.
• Узлы в графе AND/OR соответствуют задачам, а связи между узлами указывают на отношения между задачами.
• Узел, из которого исходят связи OR, представляет собой узел OR. Для решения задачи, обозначенной узлом OR, достаточно решить одну из задач его узлов-преемников.
• Узел, из которого исходят связи AND, представляет собой узел AND. Для решения задачи, обозначенной узлом AND, необходимо решить все задачи его узлов-преемников.
Часть II. Применение языка Prolog e области искусственного интеллекта
• Для указанного графа AND/OR конкретная задача формулируется с помощью
следующих двух понятий:
• начальный узел;
• целевое условие для распознавания целевых узлов.
• Целевые (или "оконечные") узлы соответствуют тривиальным (или "простейшим") задачам.
• Любое решение представлено в виде графа решения, который является подграфом графа AND/OR.
• Представление в виде пространства состояний может рассматриваться как частный случай представления в виде графа AND/OR, в котором все узлы являются узлами OR
■ Чтобы можно было воспользоваться преимуществами представления AND/OR, необходимо, чтобы узлы, связанные отношениями AND, представляли подзадачи, которые могут быть решены независимо друг от друга. Критерий независимости можно немного ослабить следующим образом: должно существовать упорядочение подзадач AND, такое, чтобы решения подзадач, встречающихся раньше при этом упорядочении, не уничтожались в результате решения последующих подзадач.
• Для обеспечения возможности сформулировать критерий оптимизации могут
быть назначены стоимости дугам или узлам, или тем и другим.
13.2. Примеры представлений в виде графа AND/OR
13.2.1. Представление в виде графа AND/OR задачи поиска маршрута
Для задачи поиска кратчайшего маршрута (см. рис, 13.1) граф AND/OR, который включает функцию стоимости, можно определить следующим образом.
• Узлы OR имеют форму X-Z, а это означает, что нужно найти кратчайший маршрут от X до Z.
• Узлы AND имеют такую форму:
X-Z via У
а это означает — найти кратчайший маршрут от X до Z, при условии, что этот маршрут должен пройти через Y.
• Узел X-Z является целевым узлом (простейшая задача), если X и z на карте соединены непосредственно.
• Стоимость каждого целевого узлаХ-2 представляет собой указанное дорожное расстояние между X и 7,.
• Стоимости всех других (нетерминальных) узлов равны 0.
Стоимость графа решения представляет собой сумму стоимостей всех узлов в графе решения (в данном случае это сумма стоимостей всех терминальных узлов). Для задачи, показанной на рис. 13.1, начальным узлом является a-z. На рис. 13.5 показано дерево решения со стоимостью 9. Это дерево соответствует маршруту [afb,d, f , i,z), который можно реконструировать из дерева решения, посетив асе листья в этом дереве в последовательности слева направо.
Глава 13. Декомпозиция задач и графы AND/OR
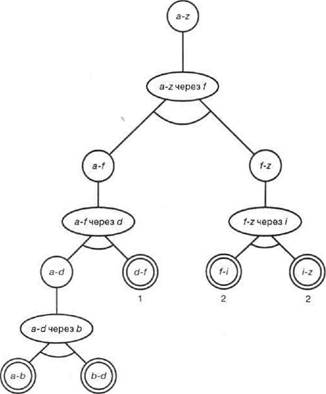 |
Рис. 13.5. Дерево решения с минимальной стоимостью для задачи поиска маршрута (см, рис. 13.1). оформленное е виде графа AND/OR
