Системы счисления и действия в них.

Рассматриваются основные понятия числовых систем, правила их построения, выполнение действий в них.

Алфавит Х из р символов и правила записи (изображения) и обработки чисел с помощью символов этого алфавита называются системой счисления (нумерацией) с основанием р. Число х в системе с основанием р обозначается как (х)_р или х_р .

Любая система счисления – это система кодирования числовых величин (количеств), позволяющая выполнять операции кодирования и декодирования, то есть по любой количественной величине однозначно находить его кодовое представление и по любой кодовой записи – восстанавливать соответствующую ей числовую величину.

Все системы счисления строятся по общему принципу: определяется величина р – основание системы, а любое число х записывается в виде комбинации степеней веса р от 0-й до n-й степени следующим образом:

(x)₁₀ = x_npⁿ + x_n–1p^n–1 + ... + x₁p¹ + x₀p⁰ .

Наиболее используемые в информатике системы счисления, кроме, естественно, десятичной, – это: 1) двоичная, над алфавитом Х = {0,1}; 2) восьмеричная, над Х = {0, 1, 2, 3, 4, 5, 6, 7}; 3) шестнадцатеричная, над Х = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, Е, F}, где символы А, В, С, D, Е, F имеют, соответственно, десятичные веса 10, 11, 12, 13, 14, 15.

Пример. 1101₂ = 1 x 2³ + 1 x 2² + 0 x 2¹ + 1 x 2⁰ = 8 + 4 + 1 = 13₁₀ ,

157₈ = 1 x 8² + 5 x 8¹ + 7 x 8⁰ = 64 + 40 + 7 = 111₁₀ ,

A6F₁₆ = 10 x 256 + 6 x 16 + 15 x 1 = 2671₁₀ .

В большинстве систем счисления вес цифры (или символа алфавита) зависит от ее места в записи числа или слова. Такая система счисления называется позиционной ; в противном случае система называется непозиционной .

Пример. Непозиционная система – древняя римская система записи чисел с алфавитом вида Х={I (1), V (5), Х (10), L (50), С (100), D (500), М (1000)}, где в скобках указаны веса символов (не зависящие от позиции символа). Примеры римских чисел (в скобках – обычные десятичные эквиваленты): III (3), IV (4), V (5), VI (6), IX (9), XI (11), DCL (650). Запись числа в этой системе получается двусторонней конкатенацией, причем правая конкатенация ассоциируется с добавлением, а левая конкатенация – с убавлением (например, IV и VI). Поразрядное же выполнение арифметических операций не имеет места (например, XIV + IV = XVIII ).

Для изображения десятичных дробей используется подобная формула разложения по степеням основания.

Пример. 110,001₂ = 1x2² + 1 x 2¹ + 0 x 2⁰ + 0 x 2^-1 + 0 x 2^-2 + 1 x 2^-3 = 6,125₁₀ ;

A,B₁₆ = A x 16⁰ + B x 16^-1 = 10 x 1 + 11 x 0,0625 = 10,6875₁₀ .

Процедура перевода десятичных чисел в р-ную систему счисления:

перевести отдельно целую часть числа х, для чего последовательно делить сперва целую часть [х]₁₀ , а затем все частные (получаемые при делении) на р до тех пор, пока не получим в очередном частном число меньшее р; изображение [х]_p получается последовательным приписыванием к последнему частному остатков от деления – от последнего до первого;

перевести отдельно дробную часть (мантиссу) числа, то есть {x}₁₀ , для чего последовательно умножать сперва исходную мантиссу, а затем мантиссы получаемых чисел на р до тех пор, пока не получим мантиссу, равную нулю, или нужное количество цифр в {х}_p ; изображение {х}_p получается приписыванием к целой части первого произведения второй такой же цифры и т.д., до последней цифры целой части;

результат будет иметь вид (х)_р = [х]_p, {х}_p .

Пример. Найти: 12,8₁₀ = ?₂ . Решение:

Переводим целую часть: 12₁₀ =1100₂;

переводим дробную часть: 0,8 x 2 = 1,6; 0,6 x 2 = 1,2; 0,2 x 2 = 0,4; 0,4 x 2 = 0,8; 0,8₁₀ = 0,1100110...₂ ;

результат перевода: 12,8₁₀ = 1100,1100110011...₂ .

Пример. Найдем 29,25₁₀ = ?₈ . Решение имеет вид 1) 29₁₀ = 35₈ ; 2) 0,25₁₀ = 0,2₈ ; 3) 29,25₁₀ = 35,2₈ .

Пример. Найдем 79,26₁₀ = ?₁₆ . Решение: 1) 79₁₀ = 4F₁₆ ; 2) 0,26₁₀ = 0,40₁₆ ; 3) 79,26₁₀ = 4F,4₁₆ . При переводе дробной части мы ограничились нахождением двух значащих цифр после запятой, ибо перевод точно сделать невозможно.

Для перевода из 2-ной в 8-ную и наоборот, из 2-ной в 16-ную и наоборот, из 8-ной в 16-ную и обратно, используется таблица следующего вида:

ОСНОВАНИЕ СИСТЕМЫ
	—
	—
	—
	—
	—
	—
	—	—
	—	—
	—	—
	—	—
	—	—
	—	—
	—	—
	—	—

При переводе в 8-ную систему или из нее необходимо группировать в тройки биты, а при переводе в 16-ную или из нее – группировать их в четверки битов. Можно добавлять, если нужно, незначащие нули (слева от целой части и справа от мантиссы) или отбрасывать их.

Пример. Рассмотрим переводы в смешанных системах.

Из 2-ной системы в 8-ную (двоично-восьмеричное изображение):

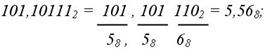
из 8-ной системы в 2–ную (восьмерично-двоичное изображение):

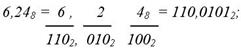
из 2-ной системы в 16-ную (двоично-шестнадцатеричное изображение):

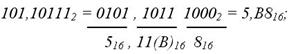
из 16-ной системы в 2-ную (шестнадцатерично-двоичное изображение):

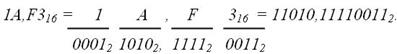
Сложение в двоичной системе счисления осуществляется по правилам

0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, 1 + 1 = 2₁₀ = 10₂ (единица идет в старший разряд).

Таблица вычитания в двоичной системе счисления имеет вид

0 – 0 = 0, 1 – 0 = 1, 1 – 1 = 0, 0 – 1 = 10 – 1 = 1 (единицу забираем у старшего разряда).

Таблица умножения в двоичной системе счисления имеет вид

0 x 0 = 0, 0 x 1 = 0, 1 x 0 = 0, 1 x 1 = 1.

Таблица деления в двоичной системе счисления имеет вид

0 : 0 = не определено, 1 : 0 = не определено, 0 : 1 = 0, 1 : 1 = 1.

Обратным кодом числа в системе с основанием р называется число в этой системе, получаемое заменой цифры, символа в каждом разряде числа на его дополнение до максимальной цифры в системе (то есть до р – 1).

Дополнительный код = обратный код + единица в младшем разряде.

Пример.

10011 двоичное число,

01100 обратный код этого двоичного числа,

01101 дополнительный код этого двоичного числа;

457 восьмеричное число,

321 дополнительный код;

А9 шестнадцатеричное число,

57 дополнительный код.

Вычитание с помощью дополнительного кода: найти дополнительный код вычитаемого такой же разрядности, как и уменьшаемое, и сложить этот код с уменьшаемым. Результатом вычитания будет полученная сумма без учета старшего разряда (отбрасывается).

Пример. Выполним вычитание напрямую и через сложение (через дополнительный код):

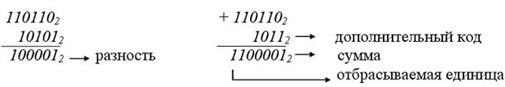
Вопросы для активизации и создания проблемной ситуации.

1. Каким образом хранится информация в компьютере?

2. Что такое бит?

3. Посчитайте сумму двоичных чисел 1001 и 1100.

4. Переведите десятичное число 120 в двоичную систему счисления.

5. В чем достоинства и недостатки Unicode?

6. Сколько потребуется бит для кодирования цветного изображения размером 320x200?

7. Каким образом кодируется звук?

8. Посчитайте, сколько килобит в мегабайте?

9. Приведите примеры текстовой информаций?

10. Приведите примеры графической информаций?

11. Приведите примеры звуковой информаций?

12. Правила перевода из одной системы счисления в другую.

Лекция №7. Организация машины (1 час)

Цель лекции: Рассмотреть архитектуру ЭВМ основанный на принципах фон Неймана; структурную организацию машины; принцип модульности, мобильности, микропрограммного управления; общую структуру машин с общей шиной, с общей памятью, с общим процессором; устройство ввода/ вывода.

Вопросы лекции:

1. Принципы фон Неймана

2. Организация машины

3. Структурная организация машины

4. Общая структура машины

5. Управляющее устройство, системы команд и типы команд.

6. Устройства ввода- вывода

7. Ввод /вывод и прерывания.

Содержание лекции:

Принципы фон Неймана Основы учения об архитектуре вычислительных машин заложил выдающийся американский математик Джон фон Нейман. Он подключился к созданию первой в мире ламповой ЭВМ ENIAC в 1944 г., когда ее конструкция была уже выбрана. В процессе работы во время многочисленных дискуссий со своими коллегами Г. Голдстайном и А. Берксом фон Нейман высказал идею принципиально новой ЭВМ. В 1946 г. ученые изложили свои принципы построения вычислительных машин в ставшей классической статье “Предварительное рассмотрение логической конструкции электронно-вычислительного устройства”. С тех пор прошло полвека, но выдвинутые в ней положения сохраняют актуальность и сегодня. В работе убедительно обосновывается использование двоичной системы для представления чисел. Авторы убедительно продемонстрировали преимущества двоичной системы для технической реализации, удобство и простоту выполнения в ней арифметических и логических операций. В дальнейшем ЭВМ стали обрабатывать и нечисловые виды информации – текстовую, графическую, звуковую и другие, но двоичное кодирование данных по-прежнему составляет информационную основу любого современного компьютера. Фон Нейман не только выдвинул основополагающие принципы логического устройства ЭВМ, но и предложил ее структуру, которая воспроизводилась в течение первых двух поколений ЭВМ. Основными блоками по Нейману являются устройство управления (УУ) и арифметико-логическое устройство (АЛУ) (обычно объединяемые в центральный процессор), память, внешняя память, устройства ввода и вывода. Схема устройства такой ЭВМ представлена на рисунке 1. Следует отметить, что внешняя память отличается от устройств ввода и вывода тем, что данные в нее заносятся в виде, удобном компьютеру, но недоступном для непосредственного восприятия человеком. Так, накопитель на магнитных дисках относится к внешней памяти, а клавиатура – устройство ввода, дисплей и печать – устройства вывода. 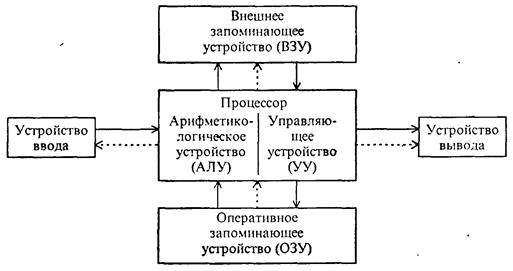  Рисунок 1. Архитектура ЭВМ, построенной на принципах фон Неймана.   Сплошные линии со стрелками указывают направление потоков информации, пунктирные – управляющих сигналов от процессора к остальными узлам ЭВМ Устройство управления и арифметико-логическое устройство в современных компьютерах объединены в один блок – процессор, являющийся преобразователем информации, поступающей из памяти и внешних устройств (сюда относятся выборка команд из памяти, кодирование и декодирование, выполнение различных, в том числе и арифметических, операций, согласование работы узлов компьютера). Более детально функции процессора будут обсуждаться ниже. Память (ЗУ) хранит информацию (данные) и программы. Запоминающее устройство у современных компьютеров “многоярусно” и включает оперативное запоминающее устройство (ОЗУ), хранящее ту информацию, с которой компьютер работает непосредственно в данное время (исполняемая программа, часть необходимых для нее данных, некоторые управляющие программы), и внешние запоминающие устройства (ВЗУ) гораздо большей емкости, чем ОЗУ. но с существенно более медленным доступом (и значительно меньшей стоимостью в расчете на 1 байт хранимой информации). На ОЗУ и ВЗУ классификация устройств памяти не заканчивается – определенные функции выполняют и СОЗУ (сверхоперативное запоминающее устройство), и ПЗУ (постоянное запоминающее устройство), и другие подвиды компьютерной памяти. В построенной по описанной схеме ЭВМ происходит последовательное считывание команд из памяти и их выполнение. Номер (адрес) очередной ячейки памяти. из которой будет извлечена следующая команда программы, указывается специальным устройством – счетчиком команд в УУ. Его наличие также является одним из характерных признаков рассматриваемой архитектуры. Разработанные фон Нейманом основы архитектуры вычислительных устройств оказались настолько фундаментальными, что получили в литературе название “фон-неймановской архитектуры”. Подавляющее большинство вычислительных машин на сегодняшний день – фон-неймановские машины. Исключение составляют лишь отдельные разновидности систем для параллельных вычислений, в которых отсутствует счетчик команд, не реализована классическая концепция переменной и имеются другие существенные принципиальные отличия от классической модели (примерами могут служить потоковая и редукционная вычислительные машины). По-видимому, значительное отклонение от фон-неймановской архитектуры произойдет в результате развития идеи машин пятого поколения, в основе обработки информации в которых лежат не вычисления, а логические выводы.

Организация машины

Анализ свойств алгоритмов позволяет выявить некоторые стандартные операции, которые встречаются наиболее часто:

ввод исходных данных;

хранение исходных и промежуточных данных;

ввод и хранение алгоритма обработки информации в виде некоторого набора элементарных операций;

выполнение арифметических и логических операций над данными (операндами);

анализ выполнения некоторых условий;

изменение хода вычислительного процесса в зависимости от результатов анализа.