Кодирование информации источника

В общем случае кодирование информации источника имеет две цели (рис. 2.2): сжатие информации (в том числе - архивация), чтобы передать большее количество информации за единицу времени; шифрование информации с целью защиты информации от несанкционированного доступа к ней. Первоначально рассмотрим сжатие информации, которое будем называть далее кодированием информации источника. Шифрование, которое будем называть криптографией, рассмотрим позднее.

2.2.1. Сжатие информации

Для сжатия информации в компьютерах используют архиваторы, например, ZIP, RAR.

В 80-х годах прошлого века разработана математическая теория сжатия. Сжатие не может быть более некоторого теоретического предела.

Чтобы определить этот предел, любое информационное сообщение длины n рассматривают как последовательность независимых одинаково распределенных дсв X или как выборку длиной n значений одной переменной X.

Показано, что для любой дси X и любого кода среднее количество бит, приходящихся на одно кодированное значение дсв, не может быть меньше энтропии этой дсв

ML(X) ³ HX.

Вместе с тем существует такое кодирование (метод Шеннона-Фано), для которого справедливо

HX ³ ML(X) – 1.

Пусть дсв X1 и дсв X2 одинаково распределены, т.е. HX1 = HX2, I(X1, X2) = 0 и

H(X1, HX2) = 2 HX1.

Вместо двух дсв можно взять одну двумерную дсв X(X1, X2). Тогда для n-мерной дсв HX = n HX1.

Пусть L1(X) = L(X)/n – количество бит на единицу сообщения X. Тогда

ML(X) – 1 ≤ HX ≤ ML(X),

ML1(X) – 1/n ≤ HX1 ≤ ML1(X).

Иначе говоря, с ростом длины n среднее количество бит на единицу сообщения будет мало отличаться от энтропии единичного сообщения.

Такой способ кодирования имеет следующие недостатки:

1) с ростом n трудоемкость построения кода становится значительной;

2) невозможна отправка сообщения по частям;

3) необходимость отправки и хранения как кода, так и сообщения исходной длины.

4) использование равномерных кодов (табл. 2.1) избыточно.

В связи с этим используют метод другие методы.

К ним относятся методы Шеннона-Фано и Хаффмена. Идея этих методов заключается в переходе от равномерных кодов к неравномерным.

Метод Шеннона-Фано. Значения дсв располагают в порядке убывания их вероятностей. Дсв разделяют на две части с приблизительно равными вероятностями. К первой части добавляют 0, ко второй – единицу, как это показано в табл. 2.1. Можно заметить, что часто встречающиеся символы стараются кодировать коротким кодом, а редко появляющиеся – длинными кодами.

Таблица 2.1

X	p(x)	Равномерный код	Неравномерный код	Code(X)
x1	1/4
x2	1/4
x3	1/8
x4	1/8
x5	1/16
x6	1/16
x7	1/16
x8	1/16

Более подробная схема кодирования представлена [3] в табл. 2.2.

Таблица 2.2

X	p(x)	Первый шаг	Второй шаг	Третий шаг	Четвер-тый шаг	Кодовое слово
x1	1/4	I	I
x2	1/4	II
x3	1/8	II	I	I
x4	1/8	II
x5	1/16	II	I	I
x6	1/16	II
x7	1/16	II	I
x8	1/16	II

Метод Хаффмена. Этот метод удобно иллюстрировать на примере, показанном в табл. 2.3.

Таблица 2.3

X	p(x)							Кодовое слово
x1	0,3
x2	0,2					0,6
x3	0,15			0,3
x4	0,15
x5	0,1		0,2		0,4
x6	0,05
x7	0,5	0,1

Нетрудно заметить, что табл. 2.3 использует дерево кодирования. Существует множество кодов-деревьев. Их совершенствование преследует цель минимального изменения дерева при появлении дополнительных букв для передачи.

Словарно-ориентированный алгоритм.Рассмотренные ранее способы кодирования относятся к статистическим методам. Словарные алгоритмы более практичны, хотя и менее обоснованы математически. Сюда относятся алгоритм LZZ, характеризующийся простотой и высокой эффективностью. Его идея заключается в том, второе и последующие вхождения некоторой строки символов сообщения заменяются ссылками на ее первое вхождение.

Недостатками LZZ являются: с ростом размеров словаря скорость работы кодера замедляется; кодирование одиночных символов неэффективно. Существуют более эффективные варианты LZZ.

Коды алгоритма LZ можно передать для кодирования алгоритму Хаффмена и получить двухшаговый конвейерный алгоритм, результаты которого подобны программам ARJ, PKZIP. Наибольшую степень сжатия дают двухпроходные алгоритмы, которые последовательно сжимают сообщение дважды, но они работают почти вдвое медленнее однопроходных алгоритмов при незначительном увеличении степени сжатия.

Для увеличения степени сжатия можно сжимать файлы в общем потоке (архиватор RAR), но это усложняет работу с архивом.

2.2.2. Криптография

Другим важным общим вопросом для источника информации является ее защита от несанкционированного доступа, т.е. придание свойства секретности при передаче информации.

Для этого существует криптография – раздел математики, в котором изучаются и разрабатываются системы изменения письма, позволяющие сделать его непонятным для непосвященных лиц.

Это особенно важно в связи с широким распространением компьютерных сетей.

Криптография – достаточно сложная наука, поэтому рассмотрим лишь ее основы.

Теоретические основы криптографии были разработаны К. Шенноном в 40-е годы прошлого века.

Существуют следующие варианты шифров информации.

1. Простая замена. Здесь система одних букв заменяется на систему других букв ил производится чтение в письме только определенных букв, например, каждой третьей, как у А. Конан Дойля в рассказе «Плящущие человечки». Такие шифры достаточно легко расшифровываются, если знать, на каком языке написано письмо. Так, в английском языке чаще всего встречается буква «о», а в английском – буква «е».

В усовершенствованных шифрах символы исходного сообщения заменяются на символы из определенного множества или текста. Они удлиняют сообщение и снижают скорость его передачи.

2. Шифры-перестановки. Например, фраза ТЕОРИЯ ИНФОРМАЦИИ разделяется на столбцы по 4 символа

ТЕОР

ИЯИН

ФОРМ

АЦИИ

Если теперь сообщение прочитать по столбцам, то получится ТИФАЕЯОЦОИРИРНМИ.

Такие шифры трудно расшифровать: необходимо знать дополнительную информацию. Однако, если удается расшифровать одно сообщение, то остальные расшифровываются легко.

Можно задавать ключевое слово, позволяющее определить порядок чтения столбцов. Например, если задать слово РЕКА, то сообщение получит вид

РЕИТ

НЯОИ

МОРФ

ИЦИА.

Нетрудно видеть, что здесь два уровня секретности: способ составления шифра и ключ. Последний может передаваться по другому засекреченному каналу.

Зашифруем ранее предложенное сообщение ключом КИБЕРНЕТИКА.

Т Е О Р И Я И Н Ф О Р М А Ц И И

20 6 16 18 10 33 10 15 22 16 18 14 1 24 10 10

К И Б Е Р Н Е Т И К А К И Б Е Р

12 10 2 6 18 15 6 20 10 12 1 12 10 2 6 18

32 16 18 24 28 15 16 2 32 28 19 26 11 26 16 28

Ю О Р Ц Ъ Н О Б Ю Ъ С Ш Й Ш О Ъ

Если использовать случайную последовательность, то шифр без ключа - нераскрываем. Проблема – в передаче ключа.

Предложена система шифрования без передачи ключа, имеющая три разновидности: без передачи ключа; с открытым ключом; электронная подпись.

Все системы построены по одному принципу, поэтому рассмотрим только шифрование без передачи ключа.

Пусть два абонента А и Б договорились о производстве закрытой переписки. Они выбирают простое и не большое число p, такое, что число (p - 1) разлагается на простые множители a и b, принимаемые абонентами А и Б. Числа a и b являются первыми секретными ключами абонентов.

Вторые ключи (a и b соответственно) находятся из уравнений aa º 1(moj(p)), 0 < a < p - 1 для А и bb º 1(modj(p)), 0 < b < p - 1. Если пересылаемое сообщение больше (p - 1), то оно разбивается на части, каждая из которых должна быть меньше (p - 1).

Пусть абонент А отправляет абоненту Б сообщение m, m < (p - 1), зашифровывая по формуле m₁ = m^a(modj(p)). Абонент Б, получив сообщение, зашифровывает его в виде m₂ = m₁^b(moj(p)) и отправляет абоненту Б. Абонент А шифрует это сообщение m₃ = m₂^a(moj(p)) и отправляет окончательно абоненту Б, который, используя ключ b, расшифровывает сообщение.

В самом деле, m₄ = m₃^a = m^aabb(modj(p)), поскольку aabb º 1 (modj(p)) и aabb = kj(p) +1 для некоторого целого k, m^{kj(p) +1} º (m^j(p))^km(modj(p)) º m из-за m^j(p) º 1 (modj(p)) по теореме Эйлера.

Пример 2.1. Пусть p = 23 (j(23) = 22), a = 5, b = 7. Из 5a = 1 (mod j(23)) получим a = 9, а из 7b = 1 (mod j(23)) имеем b = 19. Пусть m = 17.

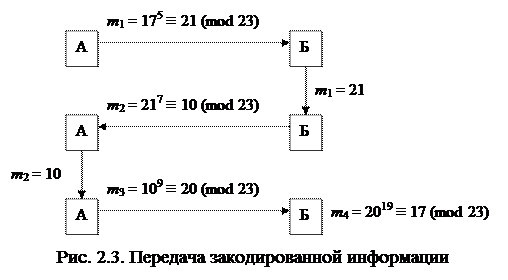Тогда передача информации может быть отражена схемой, показанной на рис. 2.3.

Кодирование сети

Рассмотрим процедуру передачи некодированных и закодированных дискретных данных по каналам связи. Отметим, что в соответствии с теоремой Котельникова частота модуляции сигнала должна не менее чем вдвое превышать частоту самого сигнала.

Характеристиками канала являются, как отмечалось, пропускная способность (емкость канала). Эффективность канала определяется скоростью передачи, достоверностью, надежностью работы и задержками сообщения.

Сообщение на выходе канала может быть искажено действием помех. Математически канал задается множеством допустимых сообщений на входе и выходе и набором условных вероятностей P(y/x) получения сигнала на y выходе при входном сигнале x. Эти вероятности описывают статистические свойства помех (шумов).

Если P(y/x) = 1 при y = x и P(y/x) = 0 при y ¹ x, то это канал без шумов. Далее речь пойдет о каналах с дискретной информацией.

Для канала без шума пропускная способность канала

C = lim(log₂N(T)/T),

^{T à ¥}

где N(T) – число возможных сигналов за время T.

Сообщения на входе в канале следует кодировать, а на выходе – декодировать при этом так, чтобы не снизить скорость передачи. Иными словами, входному алфавиту следует поставить в соответствие новый алфавит.

Теперь необходимо определить максимальную скорость передачи при наличии помехe, зная емкость канала и энтропию передатчика.

Теорема Шеннона(основная теорема о кодировании при наличии помех). Пусть источник характеризуется дсв X. Для каждого сообщения задана вероятность искажения при передаче. Тогда существует такая скорость передачи u, зависящая от X, что для любого e > 0 имеет место u¢ < u и сколь угодно близкая к u и такая, что возможно передавать сообщения со скоростью u¢ и вероятностью ошибки меньше e, u = C/HX. Этот способ позволяет получить помехоустойчивый код.

Теорема Фано(обратная теорема). Для u¢ > u можно найти такое положительное число e > 0, что при передаче информации со скоростью u¢ вероятность ошибки e передачи каждого символа сообщения при любом методе кодирования и декодирования будет не менее e, которое растет с ростом u¢.

Необходимы способы борьбы с помехами (помехозащитное кодирование). Для этого целесообразно построить математическую модель системы связи.

Удобнее всего модель иллюстрировать при передаче сообщения двоичными символами. Тогда канал можно представить в виде, показанном на рис. 2.4, где p – вероятность безошибочной передачи бита; q - вероятность передачи бита с ошибкой.

Двоичным (m, n)-кодом называется пара, состоящая из схемы кодирования E: Z₂^m à Z₂ⁿ и схемы декодирования D: Z₂ⁿ à Z₂^m, где Z₂ – множество двоичных последовательностей соответствующей длины. Обычно m < n, m = n рассматривается в криптографии. Функции D и E выбираются из условия тождественности функции H = DTE, где T – функция ошибки канала, а функции D и E считаются безошибочными (тождественными).

Для кодов вводят такие параметры.

Расстоянием Хэмминга d(a, b)между словами a и b длины n называется количество позиций кода, в которых эти слова различаются.

Вес w(a) двоичного кода a = {a_i, i = 1, n} – количество единиц в нем. Очевидно

_n

w(a) = Sa_i.

^{i = 1}

Для a = 1001, b = 0011 величины d(a, b) = 2, w(a) = w(b) = 2.

Используется операция Å поразрядного сложения без переноса (сложение по mod2, исключительное ИЛИ). Тогда d(a, b) = w(aÅb).

Вероятность того, что слово a длины n будет принято за слово b той же длины, равна p^{n – d(a, b)}q^{d(a, b)}. К примеру, вероятность принятия слова 1011 за слово 0011 составляет p³.

Напомним, что коды делят на две группы: с обнаружением и исправлением ошибок.

Чтобы код позволял обнаружить все ошибки кратности не более k, необходимо наименьшее кодовое расстояние между словами, равное k +1.

Вероятность необнаружения ошибки равна

_n

SСⁱ_n p^n-iqⁱ.

^{i = 1}

Чтобы код позволял исправить все ошибки кратности не более k, необходимо наименьшее кодовое расстояние между словами, равное 2k +1.

Вероятность ошибочного приема равна

_n

SСⁱ_n p^n-iqⁱ,

^{i = k+1}

а вероятность правильного приема

_k

SСⁱ_np^n-iqⁱ.

^{i = 0}

Показано, что (n – r, n)-код с минимальным расстоянием 2k +1 требует r дополнительных разрядов, определяемых нижней границей Хэмминга в соответствии с неравенством

r ³log₂(С^k_n + C^k-1_n + …+ C¹_n + 1).

Если имеет место нижняя граница (неравенство Варшамова-Гильберта)

r >log₂(С^2k-1_n-1 + С^2k-2_n-1 + …+ C¹_n-1 + 1),

то существует (n – r, n)-код, исправляющий ошибки кратности k и менее.

Неравенства задают необходимое и достаточное условия для построения помехоустойчивых кодов.

Простейший умозрительный код с обнаружением ошибки – добавление к байту еще одного бита, чтобы дополнить количество единиц до четного или нечетного значения.

Простейший умозрительный код, исправляющий ошибку – тройное повторение каждого бита. Если ошибка будет в одном бите, она будет исправлена. При ошибках в двух или трех битах данные будут искажены.

Если ошибки независимы, то вероятность приема n бит с k ошибками

P_n(k) = C^k_np^n-kq^k.

Пример 2.1. Пусть величина m = 2 и кодирование (функция E) осуществляется так: 00 à 000; 01 à 011; 10 à 101; 11 à 110.

Вероятность принятия сообщения хотя бы с одной ошибкой равна q³ + 3pq² + 3p²q. Вероятность правильного приема одного бита составляет p³ + 3p²q, а вероятность ошибочного приема составляет q³ + 3pq².

При использовании кода (m, 3m) сообщение может быть разбито на блоки длиной m с троекратным их повторением. Такие коды неэффективны.

Для защиты серьезных и важных сообщений необходим детальный анализ с помощью математической теория передачи данных по каналам.

Получить минимальную вероятность ошибки можно специальными кодами.

Выделяют группы блочных и древовидных (последовательных) кодов.

Можно говорить о следующих основных видах кодов.

1. Систематические коды.

2. Матричное кодирование.

3. Полиномиальные коды.

4. Циклические избыточные коды.

Систематические коды предполагают добавление к исходным кодам дополнительных контрольных символов с определенной схемой кодирования.

Матричное кодирование. Для блоков большой длины предыдущие методы требуют большое количество памяти. Имеется матрица E = (e_ij) размерности m´n. Если заданы строки кодового вектора a размерности m, то строки кодового вектора b = aE. Достаточно запомнить m кодовых слов вместо 2^m слов. Чтобы не было повторяющихся комбинаций разным значениям исходного кода, m столбцов матрицы E должны составлять единичную матрицу. Определена нижняя граница Плоткина r ³ 2d – 2 – log₂d, n ³ 2d – 2=1.

Разновидностями матричных кодов являются [1] групповые, совершенные квазисовершенные коды.

Другой разновидностью матричных кодов являются полиномиальные коды, относящиеся к блочным кодам. В полиномиальных кодах сообщению противопоставляется полином. Для кода (a₀, a₁,…, a_m-1) многочлен a(x) = a₀ + a₁x …, a_m-1x^m-1. Кодирование проводится умножением на фиксированный многочлен. Вычисления ведутся в классе вычетов по модулю 2: от результата любой арифметической операции берется остаток от его деления на 2. Разновидностью полиномиальных кодов являются циклические коды.

Циклические избыточные коды. Наибольшее распространение получили коды в 16 и 32 бита. Коды широко используются в модемах, телекоммуникационных программах, программах архивации.