Операция эквивалентность или двойная импликация

Последней введем операцию эквивалентности. Эта операция обозначается символом «, либо ~. Сложное высказываниеА«В читается: "Аэквивалентно В", либо "Аравносильно В", либо "Атогда и только тогда, когдаВ", либо "В, если и только еслиА". Эквивалентность примерно соответствует употреблению выражения "тогда и только тогда, когда", хотя, как и в случае с импликацией, такое соответствие далеко не полное.

Эквивалентность высказыванийА и В (А«В) – сложное высказывание, которое истинно, когда А и В одновременно либо истинны, либо ложны и ложно во всех других случаях. Эквивалентность определяется следующей таблицей истинности:

А	В	А«В

Эквивалентность соответствует двум операциям импликации, соединенных конъюнкцией. А«В равносильно (A®B)Ù(A®B) , т.е. имеет такую же таблицу истинности (рассмотрим это позднее). Поэтому эквивалентность также называют двойной импликацией

Логические формулы

Применяя введенные логические операции можно из простых высказываний составить высказывания сколь угодно сложного вида. Например,

A®ВÚС;

(A«Ú) ®Ù;

B®Ú (С ÙB) « (AÚB) Ù®С и т.д.

Такие высказывания называются логическими формуламиили булевыми функциями, а входящие в них простые высказывания – логическими переменными. Символы Ø, Ù, Ú, ®, « называют логическими связками.

Формулы логики высказываний можно рассматривать двояко.

ПринимаяА, В, С за обозначение простых высказываний, логическая формула будет представляться как определенное сложное высказывание. Например, если обозначитьА – «Будет дождь», В – «Я возьму зонт», С – «Я надену плащ», то A®ВÚС – запись сложного высказывания «Если будет дождь, то я возьму зонт или надену плащ».

Если рассматривать буквыА, В, С в качестве переменных, принимающих два значения 1 и 0, то в этом случае логическая формула является булевой функцией.

Для правильного вычисления значения логических формул необходимо задать порядок выполнения логических операций. Сначала выполняется операция отрицания Ø, затем конъюнкция Ù и дизъюнкция Ú (они равноправны), затем импликация ® и, последней, эквивалентность «. Как и в алгебре, скобки необходимы для изменения порядка действий, а равноправные операции вычисляются слева направо.

Таким образом, для вычисления значения выражения (A«Ú) ®Ùнеобходимо сначала определить и , затем выполнить дизъюнкцию Ú, после этого подсчитать значение выражения, стоящего в скобках: A«Ú, далее выполнить конъюнкцию высказываний Ùи, наконец, соединить вычисленные значения высказываний A«Úи Ùс помощью импликации: (A«Ú) ®Ù. Порядок выполнения операций будет таков:

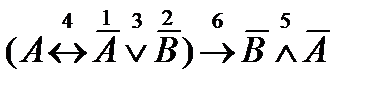Пусть простые высказыванияА и В истинны: А=1, В=1. Тогда и являются ложными высказываниями: =0, =0. Также ложной будет и дизъюнкция Ú=0. Значение высказывания в скобках A«Ú=0, так как эквивалентность истина«ложь дает ложь. Конъюнкция ложных высказываний Ùтакже ложна: Ù=0. Результирующее высказывание представляет собой соединение ложь®ложь, что по определению операции импликация есть истина. Значит, (A«Ú) ®Ù=1 приА=1 и В=1.

Вычислим значение истинности рассмотренной логической формулы при всевозможных комбинациях значений логических переменных, составляющих эту формулу. Делать такие вычисления удобнее с помощью таблицы, в каждой строке которой анализируется одна комбинация значений простых высказываний, а в столбцах вычисляются все операции по порядку. Такие таблицы, построенные для сложных высказываний, называются таблицами истинности или таблицами Куайна.

Таблица истинности – перебор всех возможных комбинаций значений простых высказываний, из которых состоит сложное, и указание соответствующих значений сложного высказывания.

Построим таблицу истинности для приведенного выше сложного высказывания:

(A«Ú) ®Ù.

Так как иА, и В могут принимать два значения, то различных комбинаций значений А и В будет четыре:

А=1, В=1;

А=1, В=0;

А=0, В=1;

А=0, В=0.

Вычислим значение сложного высказывания в каждом случае по действиям.