Практикалық жұмыс бойынша есеп беру мазмұны

1. Есептің қойылымы.

2. Математикалық моделін құру.

3. Алгоритмдік блок-схемасын құру.

4. Визуалды интерфейсті құру және өңдеу.

5. Программаның баяндалуы.

6. Программа листингі.

7. Модельдеу нәтижелерін өңдеу.

Ұсынылатын әдебиет: 1нег [18-21], 6қос [35-41], 8қос [20-22]

Практикалық жұмыс №3. Үздіксіз кездейсоқ шамаларды модельдеу

Тақырып 3.1 Үздіксіз кездейсоқ шамаларды модельдеу әдістері

Тапсырма

1. Тығыздық функциясы 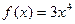болатын кездейсоқ шамасының 2 нақтыламаларын табу керек, мұнда

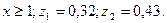
_2. Тығыздық функциясы 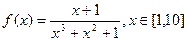түрінде берілген кездейсоқ шамасының 2 нақтыламаларын табу керек. z₁ = 0,47; z₂ = 0,24; z₃ = 0,39; z₄ = 0,75 болсын.

_3. 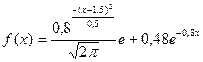тығыздық функциясымен берілген кездейсоқ шамасының нақтыламасын табу керек. z₁= 0,5; z₂= 0,8 болсын.

_4. 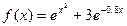тығыздық функциясымен берілген кездейсоқ шамасының нақтыламасын табу керек. z₁= 0; z₂= 1 болсын.

Практикалық сабақты өткізу түрі:жеке жоба жасау

Әдістемелік ұсыныс:

Бақылау мысалы 1. Тығыздық функциясы 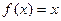болатын кездейсоқ шамасының 1 нақтыламасын табу керек, мұнда

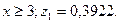
Шешуі.Есепті кері функция әдісімен шешеміз, бұл үшін х 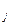қатысты теңдікті шешеміз:

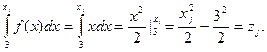
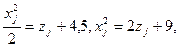
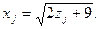
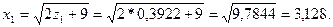
Бақылау мысалы 2. 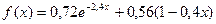тығыздық функциясымен берілген кездейсоқ шамасының нақтыламасын табу керек, 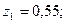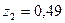болсын.

Шешуі. Тығыздық функциясы күрделі түрде болғандықтан, берілген есепті шешу үшін композиция әдісі ыңғайлы. Берілген тығыздық функциясын қарапайымдау тығыздық функцияларының композициясы ретінде қарастырайық:

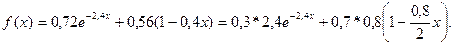
Сонымен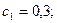

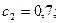
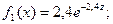
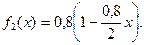
6-теореманы қолданып аламыз:

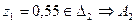оқиғасы орындалды. Сондықтан кездейсоқ шаманы модельдеу үшін f₂(x) тығыздық функциясын қолданайық, яғни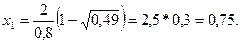

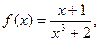
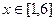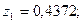
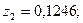
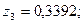
Бақылау мысалы 3. Тығыздық функциясы болатын кездейсоқ шамасының 2 нақтыламаларын табу керек, 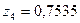болсын.

Шешуі.Есепті шешуі үшін Нейманның «шығарып тастау» әдісін қолданамыз.

М параметрін анықтайық:

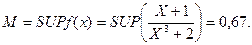
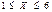
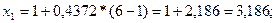
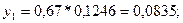
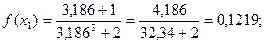
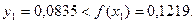
Олай болса,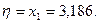

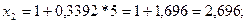
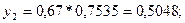
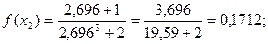
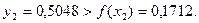
Олай болса, x₂ ескерілмейді.

Ұсынылатын әдебиет: 1нег [22-32], 3нег [506-538], 6қос [42-49], 8қос [24-29]

Тақырып 3.2 Арнаулы үлестірім заңдылықты үздіксіз кездейсоқ шамаларды модельдеу әдістері

Тапсырма

1. Тығыздық функциясы 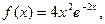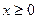түрінде болатын кездейсоқ шаманың 2 нақтыламаларын алыңыз. z мәнін шегерінділер әдісінің қысқартылған алгоритмі көмегімен есептеңіз.

2. Тығыздық функциясы 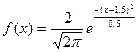түрінде болатын кездейсоқ шаманың 1нақтыламасын алыңыз. z мәнін орта көбейтінді алгоритмі көмегімен есептеңіз.

3. Тығыздық функциясы 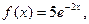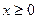түрінде болатын кездейсоқ шаманың 3 нақтыламаларын алыңыз. z мәнін шегерінділер әдісінің қысқартылған алгоритмі көмегімен есептеңіз.

4. Тығыздық функциясы 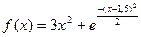түрінде болатын кездейсоқ шаманың 5 нақтыламасын алыңыз. z мәнін орта көбейтінді алгоритмі көмегімен есептеңіз.

Практикалық сабақты өткізу түрі:жеке жоба жасау

Әдістемелік ұсыныс:

Бақылау мысалы 1. Тығыздық функциясы 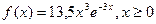түрінде болатын кездейсоқ шамасының 1 нақтыламасын алыңыз, егер ;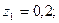

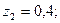
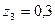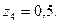
Шешуі. Тығыздық функциясы 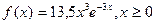түрінде болатын кездейсоқ шамасы гамма-үлестірімге бағынады. Келесі параметрлерді табайық: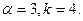

Сонымен кездейсоқ шаманың нақтыламасын келесі формуламен есептеуге болады:

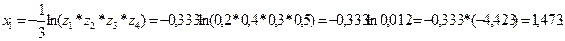
Бақылау мысалы 2. Тығыздық функциясы 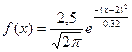болатын кездейсоқ шаманың 1 нақтыламасын алыңыз, егер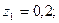

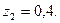
Шешуі.

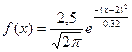түрінде тығыздық функциясы бар кездейсоқ шамасы қалыпты үлестірімге бағынады. Келесі параметрлерді табайық: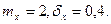

Марсаль алгоритмі көмегімен кездейсоқ шаманың нақтыламасын табамыз.

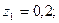
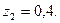
Есептейік: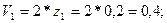

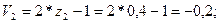
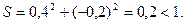
x₁ нақтыламасын келесі формуламен табамыз:

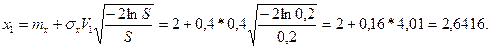
Ұсынылатын әдебиет: 1нег [22-32], 3нег [506-538], 6қос [42-49], 8қос [24-29]

Жеке тапсырмалар

Тапсырма 1

1. Тығыздық функциясы 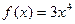болатын кездейсоқ шамасының 2 нақтыламаларын табу керек, мұнда

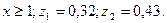
2. Тығыздық функциясы 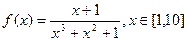түрінде берілген кездейсоқ шамасының 2 нақтыламаларын табу керек. z₁ = 0,47; z₂ = 0,24; z₃ = 0,39; z₄ = 0,75 болсын.

3. 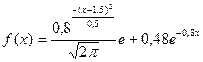тығыздық функциясымен берілген кездейсоқ шамасының нақтыламасын табу керек. z₁= 0,5; z₂= 0,8 болсын.

4. Тығыздық функциясы 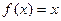болатын кездейсоқ шамасының 1 нақтыламасын табу керек, мұнда

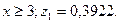
5. 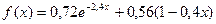тығыздық функциясымен берілген кездейсоқ шамасының нақтыламасын табу керек, 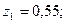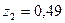болсын.

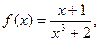
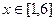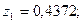
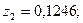
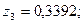
6. Тығыздық функциясы болатын кездейсоқ шамасының 2 нақтыламаларын табу керек, 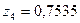болсын.

7. Тығыздық функциясы 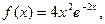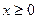түрінде болатын кездейсоқ шаманың 2 нақтыламаларын алыңыз. z мәнін шегерінділер әдісінің қысқартылған алгоритмі көмегімен есептеңіз.

8. Тығыздық функциясы 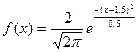түрінде болатын кездейсоқ шаманың 1 нақтыламасын алыңыз. z мәнін орта көбейтінді алгоритмі көмегімен есептеңіз.

9. Тығыздық функциясы 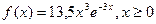түрінде болатын кездейсоқ шамасының 1 нақтыламасын алыңыз, егер ;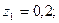

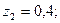
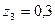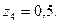
10. Тығыздық функциясы 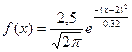болатын кездейсоқ шаманың 1 нақтыламасын алыңыз, егер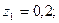

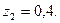
11. Тығыздық функциясы 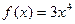болатын кездейсоқ шамасының 2 нақтыламаларын табу керек, мұнда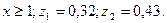

12. Тығыздық функциясы 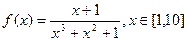түрінде берілген кездейсоқ шамасының 2 нақтыламаларын табу керек. z₁ = 0,47; z₂ = 0,24; z₃ = 0,39; z₄ = 0,75 болсын.

13. 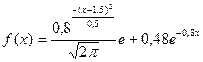тығыздық функциясымен берілген кездейсоқ шамасының нақтыламасын табу керек. z₁= 0,5; z₂= 0,8 болсын.

14. Тығыздық функциясы 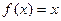болатын кездейсоқ шамасының 1 нақтыламасын табу керек, мұнда

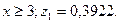
15. 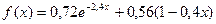тығыздық функциясымен берілген кездейсоқ шамасының нақтыламасын табу керек, 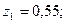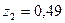болсын.

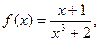
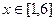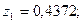
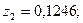
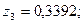
16. Тығыздық функциясы болатын кездейсоқ шамасының 2 нақтыламаларын табу керек, 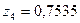болсын.

17. Тығыздық функциясы 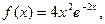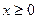түрінде болатын кездейсоқ шаманың 2 нақтыламаларын алыңыз. z мәнін шегерінділер әдісінің қысқартылған алгоритмі көмегімен есептеңіз.

18. Тығыздық функциясы 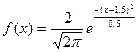түрінде болатын кездейсоқ шаманың 3 нақтыламасын алыңыз. z мәнін орта көбейтінді алгоритмі көмегімен есептеңіз.

19. Тығыздық функциясы 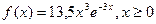түрінде болатын кездейсоқ шамасының 1 нақтыламасын алыңыз, егер ;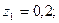

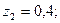
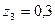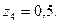
20. Тығыздық функциясы 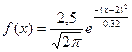болатын кездейсоқ шаманың 1 нақтыламасын алыңыз, егер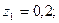

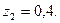
Тапсырма 2

1. Гамма-үлестірімінің компьютерлік моделін құру

2. Сызықтық үлестірімінің компьютерлік моделін құру

3. Қалыпты үлестірімінің компьютерлік моделін құру

4. Вейбулл үлестірімінің компьютерлік моделін құру

5. Логарифмді-қалыпты үлестірімінің компьютерлік моделін құру

6. Бета-үлестірімінің компьютерлік моделін құру

7. Пирсон үлестірімінің компьютерлік моделін құру

8. Логарифмді-логистикалық үлестірімінің компьютерлік моделін құру

9. Джонсонның байланысты үлестірімінің компьютерлік моделін құру

10. Джонсонның байланыссыз үлестірімінің компьютерлік моделін құру

11. Безье үлестірімінің компьютерлік моделін құру

12. Үшбұрышты үлестірімінің компьютерлік моделін құру

13. Эмпирикалық үлестірімінің компьютерлік моделін құру

14. Бернулли үлестірімінің компьютерлік моделін құру

15. Дискретті бірқалыпты үлестірімінің компьютерлік моделін құру

16. Биномиалды үлестірімінің компьютерлік моделін құру

17. Теріс биномиалды үлестірімінің компьютерлік моделін құру

18. Бірқалыпты үлестірімінің компьютерлік моделін құру

19. Экспоненциалдық үлестірімінің компьютерлік моделін құру

20. Гаусс үлестірімінің компьютерлік моделін құру