Этапы имитационного моделирования
Как уже отмечалось, имитационное моделирование применяют для исследования сложных экономических систем. Естественно, что и имитационные модели оказываются достаточно сложными как с точки зрения заложенного в них математического аппарата, так и в плане машинной реализации. При этом сложность любой модели определяется двумя факторами: сложностью исследуемого объекта-оригинала; точностью, предъявляемой к результатам расчетов.
Использование машинного эксперимента как средства решения сложных прикладных проблем, несмотря на присущую каждой конкретной задаче специфику, имеет ряд общих черт (этапов). На рис. 11.1 представлены этапы применения математической (имитационной) модели (по взглядам академика А. А. Самарского).
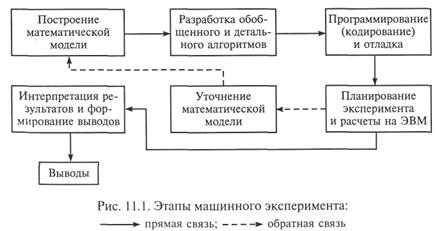
Каждому из показанных на рисунке этапов присущи собственные приемы, методы, технологии. В данном учебнике вопросы построения (разработки) математической модели, алгоритмизации и программирования (за исключением выбора языка) не рассматриваются. Отметим лишь, что все эти этапы носят ярко выраженный творческий характер и требуют от разработчика модели особой подготовки.
После того как имитационная модель реализована на ЭВМ, исследователь должен выполнить последовательность следующих этапов (их часто называют технологическими) [29, 55]:
· испытание модели;
· исследование свойств модели;
· планирование имитационного эксперимента;
· эксплуатация модели (проведение расчетов).
Кратко охарактеризуем первые два этапа (изложение методов математической теории планирования эксперимента и организации проведения модельных расчетов и обработки их результатов выходят за рамки настоящего учебника).
Испытание имитационной модели.Включает работы по четырем направлениям:
· задание исходной информации;
· верификацию имитационной модели;
· проверку адекватности модели;
· калибровку имитационной модели.
Задание исходной информации. Процедура задания исходной информации полностью определяется типом моделируемой системы:
· если моделируется функционирующая (существующая) система, проводят измерение характеристик ее функционирования и затем используют эти данные в качестве исходных при моделировании;
· если моделируется проектируемая система, проводят измерения на прототипах;
· если прототипов нет, используют экспертные оценки параметров и переменных модели, формализующих характеристики реальной системы.
Каждому из этих вариантов присущи собственные особенности и сложности. Так, проведение измерений на существующих и проектируемых системах требует применения качественных измерительных средств, а проведение экспертного оценивания исходных данных представляет собой комплекс достаточно сложных процедур получения, обработки и интерпретации экспертной информации.
Верификация имитационной модели. Она состоит в доказательстве утверждений соответствия алгоритма ее функционирования цели моделирования путем формальных и неформальных исследований реализованной программы модели.
Неформальные исследования представляют собой ряд процедур, входящих в автономную и комплексную отладку.
Формальные методы включают:
· использование специальных процессоров-«читателей» программ;
· замену стохастических элементов модели детерминированными;
· тест на так называемую непрерывность моделирования и др.
Проверка адекватности модели. Количественную оценку адекватности модели объекту исследования проводят для случая, когда можно определить значения отклика системы в ходе натурных испытаний.
Наиболее распространены три способа проверки:
· по средним значениям откликов модели и системы;
· дисперсиям отклонений откликов;
· максимальному значению абсолютных отклонений откликов.
Если возможность измерения отклика реальной системы отсутствует, оценку адекватности модели проводят на основе субъективного суждения соответствующего должностного лица о возможности использования результатов, полученных с использованием этой модели, при выполнении им служебных обязанностей (в частности, при обосновании решений — подробнее см. [53]).
Калибровка имитационной модели. К калибровке имитационной модели приступают в случае, когда модель оказывается неадекватной реальной системе. За счет калибровки иногда удается уменьшить неточности описания отдельных подсистем (элементов) реальной системы и тем самым повысить достоверность получаемых модельных результатов.
В модели при калибровке возможны изменения трех типов:
· глобальные структурные изменения;
· локальные структурные изменения;
· изменение так называемых калибровочных параметров в результате реализации достаточно сложной итерационной процедуры, включающей многократное построение регрессионных зависимостей и статистическую оценку значимости улучшения модели на очередном шаге.
При необходимости проведения некоторых локальных и особенно глобальных структурных изменений приходится возвращаться к содержательному описанию моделируемой системы и искать дополнительную информацию о ней.
Исследование свойств имитационной модели.После испытаний имитационной модели переходят к изучению ее свойств. При этом наиболее важны четыре процедуры:
· оценка погрешности имитации;
· определение длительности переходного режима в имитационной модели;
· оценка устойчивости результатов имитации;
· исследование чувствительности имитационной модели.
Оценка погрешности имитации, связанной с использованием в модели генераторов ПСЧ. Исследование качества генераторов ПСЧ проводится известными методами теории вероятностей и математической статистики (см. подразд. 10.1). Важнейшим показателем качества любого генератора ПСЧ является период последовательности ПСЧ (при требуемых статистических свойствах). В большинстве случаев о качестве генератора ПСЧ судят по оценкам математических ожиданий и дисперсий отклонений компонент функции отклика. Как уже отмечалось, для подавляющего числа практических задач стандартные (встроенные) генераторы дают вполне пригодные последовательности ПСЧ.
Определение длительности переходного режима. Обычно имитационные модели применяются для изучения системы в типичных для нее и повторяющихся условиях. В большинстве стохастических моделей требуется некоторое время Т0 для достижения моделью установившегося состояния.
Под статистическим равновесием или установившимся состоянием модели понимают такое состояние, в котором противодействующие влияния сбалансированы и компенсируют друг друга. Иными словами: модель находится в равновесии, если ее отклик не выходит за предельные значения.
Существует три способа уменьшения влияния начального периода на динамику моделирования сложной системы:
· использование «длинных прогонов», позволяющих получать результаты после заведомого выхода модели на установившийся режим;
· исключение из рассмотрения начального периода прогона;
· выбор таких начальных условий, которые ближе всего к типичным.
Каждый из этих способов не свободен от недостатков: «длинные прогоны» приводят к большим затратам машинного времени; при исключении из рассмотрения начального периода теряется часть информации; выбор типичных начальных условий, обеспечивающих быструю сходимость, как правило, затруднен отсутствием достаточного объема исходных данных (особенно для принципиально новых систем).
Для отделения переходного режима от стационарного у исследователя должна быть возможность наблюдения за моментом входа контролируемого параметра в стационарный режим. Часто используют такой метод: строят графики изменения контролируемого параметра в модельном времени и на нем выявляют переходный режим. На рис. 11.2 представлен график изменения k-гoконтролируемого параметра модели gk в зависимости от модельного времени t0. На рисунке видно, что, начиная со времени tперех, этот параметр «вошел» в установившийся режим со средним значением k.
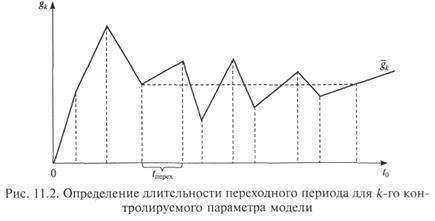
Если построить подобные графики для всех (или большинства существенных) контролируемых параметров модели, определить для каждого из них длительность переходного режима и выбрать из них наибольшую, в большинстве случаев можно считать, что после этого времени все интересующие исследователя параметры находятся в установившемся режиме.
На практике встречаются случаи, когда переходные режимы исследуются специально. Понятно, что при этом используют «короткие прогоны», исключают из рассмотрения установившиеся режимы и стремятся найти начальные условия моделирования, приводящие к наибольшей длительности переходных процессов. Иногда для увеличения точности результатов проводят замедление изменения системного времени.
Оценка устойчивости результатов имитации. Под устойчивостью результатов имитации понимают степень их нечувствительности к изменению входных условий. Универсальной процедуры оценки устойчивости нет. Практически часто находят дисперсию отклика модели У по нескольким компонентам и проверяют, увеличивается ли она с ростом интервала моделирования. Если увеличения дисперсии отклика не наблюдается, результаты имитации считают устойчивыми.
Важная практическая рекомендация: чем ближе структура модели к структуре реальной системы и чем выше степень детализации учитываемых в модели факторов, тем шире область устойчивости (пригодности) результатов имитации.
Исследование чувствительности модели. Работы на этом этапе имеют два направления:
· установление диапазона изменения отклика модели при варьировании каждого параметра;
· проверка зависимости отклика модели от изменения параметров внешней среды.
В зависимости от диапазона изменения откликов Y при изменении каждой компоненты вектора параметров X определяется стратегия планирования экспериментов на модели. Если при значительной амплитуде изменения некоторого компонента вектора параметров модели отклик меняется незначительно, то точность представления ее в модели не играет существенной роли.
Проверка зависимости отклика модели Y от изменений параметров внешней среды основана на расчете соответствующих частных производных и их анализе.
Языки моделирования
Чтобы реализовать на ЭВМ модель сложной системы, нужен аппарат моделирования, который в принципе должен быть специализированным. Он должен предоставлять исследователю:
· удобные способы организации данных, обеспечивающие простое и эффективное моделирование;
· удобные средства формализации и воспроизведения динамических свойств моделируемой системы;
· возможность имитации стохастических систем, т.е. процедур генерации ПСЧ и вероятностного (статистического) анализа результатов моделирования;
· простые и удобные процедуры отладки и контроля программы;
· доступные процедуры восприятия и использования языка и др.
Вместе с тем существующие языки программирования общего назначения (ЯОН) для достаточно широкого круга задач позволяют без значительных затрат ресурсов создавать весьма совершенные имитационные модели. Можно сказать, что они способны составить конкуренцию специализированным языкам моделирования. Для систематизации представлений о средствах реализации имитационных моделей приведем основные определения и краткие сведения о подходах к выбору соответствующего языка. Языком программирования называют набор (систему) символов, распознаваемых ЭВМ и обозначающих операции, которые можно реализовать на ЭВМ. Выделяют машинно-ориентированные, проблемно (процедурно)-ориентированные и объектно-ориентированные языки.
Классические языки моделирования являются процедурно-ориентированными и обладают рядом специфических черт. Можно сказать, что основные языки моделирования разработаны как средство программного обеспечения имитационного подхода к изучению сложных систем.
Языки моделирования позволяют описывать моделируемые системы в терминах, разработанных на базе основных понятий имитации. С их помощью можно организовать процесс общения заказчика и разработчика модели. Различают языки моделирования непрерывных и дискретных процессов.
В настоящее время сложилась ситуация, когда не следует противопоставлять ЯОН и языки имитационного моделирования (ЯИМ). На рис. 11.3 представлена классификация языков программирования по различным основаниям, которая может служить основой для формирования рационального подхода к выбору конкретного языка реализации имитационной модели исследуемой ЭИС, о чем будет подробнее сказано ниже [48].
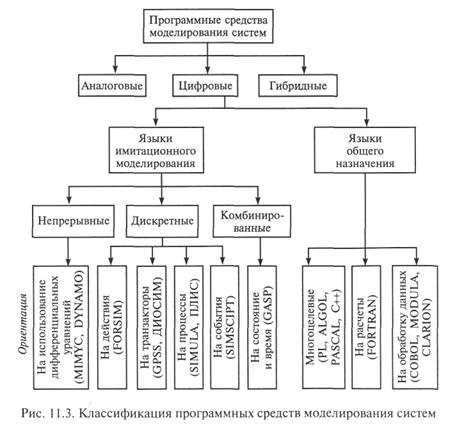
Легко заметить из названий, что некоторые ЯИМ базируются на конструкциях ЯОН: например, FORSIM — на языке FORTRAN; ПЛИС — на языке PL и т.д.
В силу своего целевого назначения при правильном выборе и использовании языки моделирования обладают рядом неоспоримых достоинств.
Вместе с тем им присущи и определенные недостатки, главными из которых являются сугубо индивидуальный характер соответствующих трансляторов, затрудняющий их реализацию на различных ЭВМ; низкая эффективность рабочих программ; сложность процесса отладки программ; нехватка документации (литературы) для пользователей и специалистов-консультантов и др. В ряде случаев эти недостатки способны перечеркнуть любые достоинства.
Существует несколько подходов к выбору языка, на котором будет реализовываться разрабатываемая имитационная модель. Предлагается классическая двухэтапная схема выбора, имеющая широкое практическое применение.
На первом этапе следует найти ответы на следующие вопросы.
1. Имеются ли хорошо написанные руководства и инструкции для пользователей?
2. Совместим ли язык транслятора с имеющимися ВС?
3. Можно ли данный язык использовать на других ВС, способных решать задачи пользователя?
4. Обеспечивает ли транслятор языка выдачу информации об ошибках и глубокую их диагностику?
5. Насколько эффективен данный язык с учетом общего времени подготовки, программирования, отладки программы, компиляции и прогона ее на ЭВМ?
6. Какова стоимость внедрения, эксплуатации и обновления ПО для данного языка?
7. Знаком ли язык и, если нет, легко ли его изучить?
8. Оправдает ли частота использования языка в различных будущих моделях затраты на его изучение и освоение?
По результатам ответов на данные вопросы, как правило, отбирается несколько языков. Окончательный выбор основывается на учете характеристик конкретной задачи при ее решении на определенной машине.
Второй этап выбора предусматривает поиск ответов на такие вопросы.
1. Какова область применения языка и его пригодность для описания явлений реального мира (методы прогнозирования; ориентация; способность генерировать случайные факторы)?
2. Насколько легко осуществляется хранение и извлечение данных, характеризующих состояния системы и работу отдельных ее частей?
3. Обеспечивается ли необходимая гибкость и каковы возможности языка в отношении модифицирования состояний системы?
4. Насколько легко данный язык может описывать динамическое поведение?
5. Каковы выходные формы документов, чем они полезны и какой статистический анализ возможен на основе этих данных?
6. Насколько просто вставлять в модель стандартные подпрограммы, написанные пользователями?
Приведенные вопросы можно конкретизировать или расширять с учетом современного уровня и перспектив развития технических, программных средств и информационных технологий, но изложенный подход к выбору языка является неизменно актуальным и конструктивным.
Если попытаться обобщить направленность данных вопросов, то можно заметить, что важнейшими проблемами применения языков моделирования являются их эффективность, совместимость с другими программными средствами и возможность установки на имеющиеся технические средства, а также затраты различных ресурсов. Иными словами, при выборе программного средства моделирования следует руководствоваться известным критерием «эффективность — время — стоимость», причем зачастую важность каждого из этих частных показателей меняется в зависимости от существа задачи; объема располагаемых ресурсов; резерва (дефицита) времени; сложившихся условий и т. п. Вообще говоря, данная рекомендация справедлива для выбора весьма широкого круга сложных объектов различной природы.
