Двоичная стеганосистема передачи скрываемых сообщений

Определим величину скрытой ПС стеганосистемы, в которой алфавит скрываемых сообщений, ключей и стеганограмм двоичный: m=c=k=s= {0;1} [5, 61]. Пусть контейнер с формируется источником Бернулли с параметром р=0,5 (то есть двоичные символы последовательности контейнера равномерны и независимы друг от друга). Функция искажения d₁=d₂ описывается расстоянием Хемминга: d(x,y) = 0, если х=у и d(x,y) = 1, если .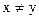

Описание контейнера является секретным ключом стеганосистемы (k=с) и известно получателю. Пусть стеганограммы формируются в виде 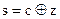, где операция " 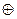" — это сложение по модулю 2. Очевидно, что переменная z будет иметь распределение Бернулли и отображать скрываемое сообщение m с искажением А₁.

Искажение А₁ означает, что каждый символ двоичной последовательности z отличается от соответствующего символа двоичной последовательности m с вероятностью А₁. Преобразование сообщения m в последовательность z выполняется передающей стороной с использованием кодера с искажением А₁. Нарушитель обрабатывает стеганограмму наложением на нее двоичной шумовой последовательности а, в которой единичный символ порождается с вероятностью А₂. Получатель суммирует искаженную стеганограмму 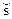с двоичной последовательностью с по модулю 2, и из полученной таким образом двоичной последовательности 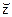декодирует принятое скрываемое сообщение .

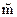Особенность такой стеганосистемы заключается в том, что скрываемое в ней сообщение при встраивании искажается с вероятностью искажения А₁, и это искажение равно искажению кодирования стеганограммы. Описанная стеганограмма изображена на рис. 4.2.

Рис 4.2. Структурная схема двоичной стеганосистемы

Утверждение 4.3

Для двоичной стеганосистемы при уровнях искажений 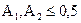скрытая пропускная способность определяется как

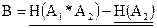
где 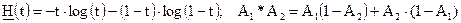(4.15)

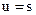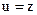Для данной стеганосистемы переменную и можно формировать как или и -причем оба варианта могут быть оптимальными, поскольку в качестве операции встраивания используется операция суммирования по модулю 2 [5].

Оптимальная атака нарушителя определяется в виде 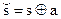, где а — случайная двоичная последовательность, распределенная по закону Бернулли с вероятностью появления единичного символа —А₂

При уровнях искажени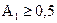й и 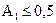СПС равна 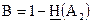. Если 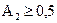, СПС равна нулю.

Необходимо отметить, что при А₁= 0,5 СПС не равна нулю независимо от значения 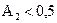. Это объясняется тем, что при преобразовании скрываемого сообщения m в последовательность z искажение не равновероятно: лицо, которое скрывает информацию, может избрать такое распределение ошибок А₁, при котором будет минимизироваться переменная сообщения m. Для А₂=0,5 СПС будет равна нулю при любых значениях A_1.

Несложно заметить, что в этом случае выход 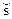канала не зависит от его входа s, что означает разрыв канала связи. А если при обрыве канала связи невозможна передача по открытому каналу связи, то тем более невозможна и передача по скрытому каналу, образованному на основе открытого.

Применим следствие теоремы (4.1) для анализа двоичной стеганосистемы. Пусть 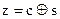, 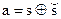. Платежная функция имеет вид 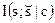. Допустим, что .

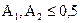Шаг 1.

Зафиксируем 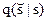Для всех 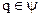, получим

(a) (b)

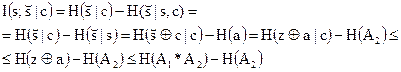(c)

где равенство (а) справедливо относительно определения условного взаимодействия информации; (b) выполняется благодаря тому, что 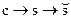— марковская цепь; неравенство (с) справедливо, поскольку условие уменьшает энтропию. Равенство в (с) достигается тогда и только тогда, когда 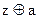, следовательно, z независима от с. Неравенство (d) справедливо, поскольку z и а независимы (в силу того, что 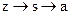формирует маковскую цепь и 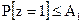. Равенство (d) достигается, если переменная z имеет распределение Бернулли с дисперсией А₁. Распределение 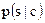удовлетворяет обоим нестрогим неравенствам и поэтому максимизирует значение .

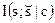Шаг 2.

Зафиксируем 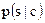. Будем минимизировать 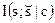над 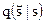При определенном ранее распределении 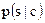, z и s независимы. Поскольку 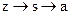формирует марковскую цепь, z и a также независимы. Имеем

(e)

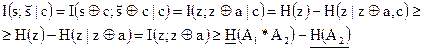(f)

где неравенство (е) справедливо, поскольку условие уменьшает энтропию; неравенство (f) справедливо, потому что z и a независимы и 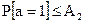(что становится равенством, когда а — переменная с распределением Бернулли с вероятностью единичного символа A₂).

Рассмотренная двоичная стеганосистема похожа на систему шифрования однократной подстановки (шифр гаммирования с бесконечной равновероятностной независимой шифрующей гаммой). При независимой и равномерной последовательности с выполняется равенство 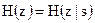, означающее, что данная система удовлетворяет требованию относительно идеальных криптосистем [60]. Следовательно, перехват и анализ криптограммы s не дает атакующему никакой информации относительно защищаемого сообщения s.

Кроме этого, указанная двоичная система удовлетворяет также требованию относительно идеальных стеганосистем: распределения р(с) и p(s) идентичны, поэтому нарушитель не в состоянии определить, принадлежат ли перехваченные им данные к распределению 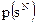пустых контейнеров или же к распределению 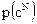стеганограммы со встроенным сообщением [15]. Однако при этом отмечается, что в рассмотренной стеганосистеме предусматривается описание контейнеров и, соответственно, стеганограмм распределением Бернулли, а это зачастую нехарактерно для реальных систем скрытия информации [S].

Рассмотрим пример двоичной стеганосистемы с выбором u=z. Пусть существует необходимость в скрытой передаче сообщения m, которое представляет собой оцифрованный речевой сигнал с количеством уровней квантования 8. В общем виде скрываемое сообщение может быть представлено в виде .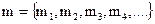

Пусть первые несколько отсчетов сообщения в моменты времени дискретизации 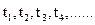принимают десятичные значения 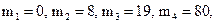(рис. 4.3, а).

В двоичной форме скрываемое сообщение запишем как

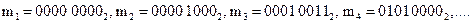
Преобразуем двоичную последовательность m в двоичную последовательность z с погрешностью А₁. B двоичной системе погрешность кодирования А₁ вычисляется по метрике Хеммннга. Пусть А₁=1/8. Следовательно, для формирования последовательности 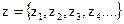лицо, скрывающее информацию, искажает восьмую часть битов последовательности m. Для уменьшения искажения скрываемого сообщения ему целесообразно искажать только младшие биты двоичной последовательности m.

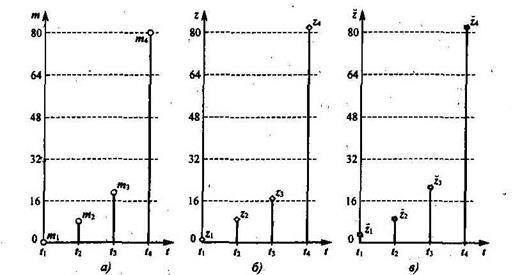
Рис. 4.3. Пример двоичной стеганосистемы с искажениями А₁=1/8 и А₂=1/16

Пусть скрывающий информацию избрал последовательность z следующего вида:

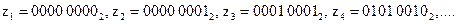
В десятичном виде последовательность z изображена на рис. 4.3, б.

Допустим, что с помощью генератора ПСЧ был сформирован секретный ключ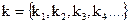

Отправитель по правилу 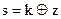формирует стеганосистему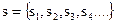

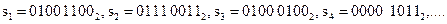
Пусть искажение А₂=1/16. Нарушитель случайно формирует двоичную последовательность 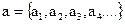, в которой вероятность появления единичных символов составляет А₂. Например:

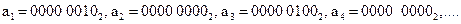
Атакующее воздействие — это сложение по модулю 2 стеганограммы s и шумовой последовательности а. Следовательно, искаженная стеганограмма 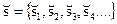будет иметь следующий вид:

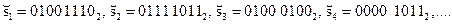
Получатель для формирования принятого сообщения 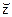прибавляет по модулю 2 последовательность 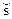к последовательности ключа k:

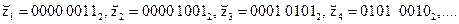
В декодере получатель из данной последовательности восстанавливает сообщение m. В простейшем случае 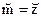. Вид последовательности 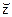изображен на рис. 4.3, в.

Если скрываемое сообщение m представляет собой речевой сигнал, то при указанных величинах искажений А₁ и А₂ степень приближенности 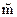к m (то есть, качество обеспечиваемой скрытой телефонной связи), для ряда телекоммуникационных задач может быть оценена как удовлетворительная.

Выводы

В данной главе введено одно из ключевых понятий теории передачи информации и, в частности, стеганографических систем (как каналов скрытого обмена данными) — пропускная способность канала передачи скрываемых данных. В процессе обработки зарубежных и отечественных литературных источников выделено два основных подхода к оценке ПС стеганосистем.

Подход, ориентированный на стеганосистемы, в которых скрытые сообщения должны быть безошибочно переданы адресату в условиях активного противодействия нарушителя. При этом учитывается, что кроме искажений: контейнера при встраивании в него конфиденциальных данных, вероятны намеренные его искажения со стороны активного нарушителя и/или искажения, вызванные случайными помехами в канале связи.

• Подход, ориентированный на стеганосистемы, в которых реализуется скрытая передача априорно неизвестной получателю информации, причем пассивный нарушитель пытается в процессе наблюдения обнаружить факт наличия канала скрытой связи и, в случае успеха, стремится раскрыть содержание скрытых данных.

• В рамках первого подхода представлены основные задачи информационного скрытия в случае активного противодействия нарушителя; описано скрывающее преобразование, выполняемое при встраивании информации в контейнер, и атакующее воздействие, совершаемое нарушителем для противодействия скрытой передаче; рассмотрена основная теорема информационного скрытия при активном противодействии нарушителя; приведено определение величины скрытой ПС двоичной стеганосистемы.

На основании этого рассмотрены основные свойства скрытой пропускной способности стеганоканала, приведены комментарии о полученных результатах, что позволило заложить обоснованную теоретическую базу для разработки систем стеганографического скрытия конфиденциальной информации.

Глава 5