Динамическое программирование. Алгоритм нахождения кратчайшего пути Дейкстры

Динамическое программирование

Нередко не удается разбить задачу на небольшое число подзадач, объединение решений которых позволяет получить решение исходной задачи. В таких случаях мы можем попытаться разделить задачу на столько подзадач, сколько необходимо, затем каждую подзадачу разделить на еще более мелкие подзадачи и т.д. Если бы весь алгоритм сводился именно к такой последовательности действий, мы бы получили в результате алгоритм с экспоненциальным временем выполнения. Но зачастую удается получить лишь полиномиальное число подзадач и поэтому ту или иную подзадачу приходится решать многократно. Если бы вместо этого мы отслеживали решения каждой решенной подзадачи и просто отыскивали в случае необходимости соответствующее решение, мы бы получили алгоритм с полиномиальным временем выполнения.

С точки зрения реализации иногда бывает проще создать таблицу решений всех подзадач, которые нам когда-либо придется решать. Мы заполняем эту таблицу независимо от того, нужна ли нам на самом деле конкретная подзадача для получения общего решения. Заполнение таблицы подзадач для получения решения определенной задачи получило название динамического программирования (это название происходит из теории управления).1

Алгоритм Кратчайший путь из одного источника (алгоритм Дейкстры)

В задаче нахождения кратчайших путей из одного источника ситуация иная. Хотя нет причин предполагать, что для ее решения понадобится более 0(е) времени, ни один такой алгоритм не известен. Мы обсудим алгоритм сложности 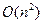, работа которого основана на построении множества S узлов, кратчайшие расстояния до которых от источника известны. На каждом шаге к S добавляется тот из оставшихся узлов, скажем и, расстояние до которого от источника меньше всех других оставшихся узлов. Если стоимости всех ребер неотрицательны, то можно быть уверенным, что путь из источника в v проходит только через узлы из S. Поэтому достаточно найти для каждого узла v кратчайшее расстояние до него от источника вдоль пути, проходящего только через узлы из S.

Вход. Ориентированный граф G== (V, Е), источник 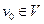и функция 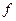, отображающая множество ЕхЕ в множество неотрицательных вещественных чисел. Полагаем 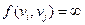, если 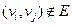и ,

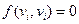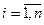
Метод: Строим такое множество вершин 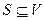, что кратчайший путь из источника в каждый узел 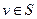целиком лежит в . Элемент 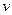массива содержит стоимость кратчайшего пути ведущего из 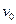в 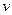, который проходит только через узлы из .

Продолжение 28

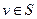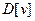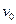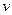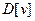Чтобы показать корректность, надо доказать индукцией по размеру множества S, что для каждого ребра число равно длине кратчайшего пути из в . Более того, для всех число равно длине кратчайшего пути из 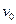в 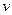, лежащего целиком (если не считать сам узел v) в S.

Базис. Пусть ||S|| = 1. Кратчайший путь из 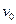в себя имеет длину 0, а путь из 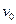в 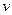, лежащий целиком (исключая 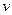) в S, состоит из единственного ребра 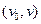. Таким образом, строки 2 и 3 корректно формируют начальные значения массива D.

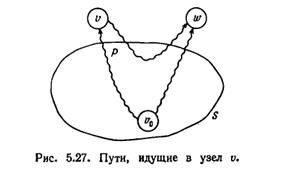
Шаг индукции. Пусть w — узел, выбранный в строке 5. Если число D[w] не равно длине кратчайшего пути из v0 в w, то должен быть более короткий путь Р. Этот путь Р должен содержать некоторый узел, отличный от w и не принадлежащий S. Пусть v - первый такой узел на Р. Но тогда расстояние от 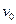до 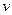меньше D[w], а кратчайший путь в 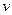целиком (исключая сам узел и) лежит в S. Следовательно, по предположению индукции 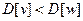в момент выбора w, пришли к противоречию. Отсюда заключаем, что такого пути Р нет и 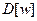— длина кратчайшего пути из 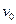в w. Второе утверждение (о том, что 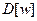остается корректным) очевидно ввиду строки 8.