Устойчивость стеганосистем к пассивным атакам

Пассивный нарушитель пытается найти ответ на вопрос: содержит перехваченный им контейнер скрытую информацию или нет? Для этого ему необходимо провести оценку неоднородности некоторых параметров контейнера, обнаружить в нем "подозрительные" участки, завышенное зашумление н другие следы присутствия скрытых сообщений. Эта задача может быть формализована в виде проблемы проверки статистических гипотез [5]. С этой целью вводят тестовую функцию стеганодекодера; которая, в зависимости от типа последнего, может выдавать двухразрядные (в более сложном случае — 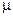-разрядные) решения о наличии/отсутствии встроенного сообщения:

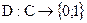(3.20)

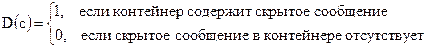
С помощью данной функции нарушитель способен оценивать сообщения, перехваченные им в несекретном канале. В качестве детектора скрытых сообщений зачастую используют корреляционный приемник, изображенный на рис. 3.3.

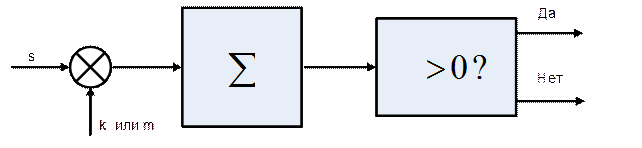
Рис. 3.3. Корреляционный детектор скрытых сообщений

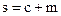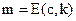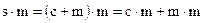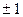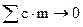Пусть вследствие скрытия в изображении-контейнере сообщения, у некоторой части пикселей значение яркости было увеличено на 1, а у других осталось неизменным, или же было уменьшено на 1. Тогда , где . Коррелятор детектора вычисляет величину . Поскольку m принимает значение , то , a 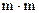всегда будет положительным, поэтому 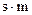будет очень близким к 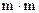. Тогда можно воспользоваться сведениями из теории cвязи и записать вероятность ошибочного обнаружения наличия скрытого сообщения как дополнительную (комплементарную) функцию ошибок от корня квадратного из отношения 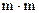("энергии сигнала") к дисперсии значений пикселей яркости ("энергия шума") [5].

В детекторе возможно возникновение двух типов ошибок. Существует вероятность того, что при анализе контейнера детектор не обнаружит присутствующего в нем скрытого сообщения ( 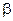-вероятность пропуска цели или так называемая ошибка 2-го рода), а также вероятность ошибочного обнаружения скрытого сообщения в пустом контейнере ( 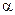-вероятность Ложной тревоги или так называемая ошибка 1-го рода). Уменьшение одной вероятности приводит к возрастанию другой. На практике пытаются максимизировать для пассивного атакующего ошибку 2-го рода, идеальная же стеганосистема должна обеспечивать ошибку 2-го рода 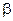= 1. Ниже будет показано, что все абсолютно надежные стеганосистемы имеют это свойство (при условии, что атакующий совершает ошибку 1 -го рода с вероятностью 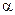= 0).

Для 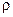-надежных стеганографических систем вероятность 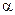и 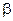связаны между собой в соответствии с представленной ниже теоремой [15]

Теорема 3.2

Пусть 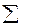— стеганографическая система, которая является 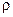-надежной против пассивных атак. Тогда вероятность 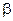того, что нарушитель не обнаружит скрытое сообщение, и вероятность 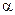того, что он ошибочно обнаружит несуществующее скрытое сообщение, удовлетворяют соотношению 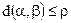, где 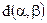— относительная двоичная энтропия, которая определяется как

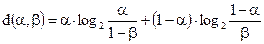(3.22)

В частности, если 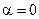, то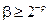

Доказательство

В случае, когда контейнеры не содержат скрытого сообщения, то их распределение вероятностей соответствует Р_с. Рассмотрим случайную величину f(С) и вычислим ее вероятность 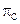. Если f(С)=1 (пустой контейнер принимается за стеганограмму), нарушитель совершает ошибку 1 -го рода. Таким образом, 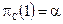и .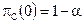

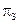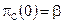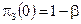Если контейнер содержит скрытое сообщение, то распределение вероятностей соответствует Р_S. Вычислим вероятность для f(С). В случае, когда f(С)=0 (стеганограмма принимается за пустой контейнер), нарушитель совершает ошибку 2-го рода. Следовательно, и . Относительная энтропия 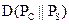в соответствии с (3.20) может быть выражена следующим образом:

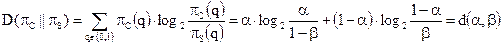
Отметим следующее свойство функции относительной энтропии: детерминированная обработка не может увеличить относительную энтропию между двумя распределениями. Пусть Q₀ и Q₁ — две случайные величины, определенные на множестве наблюдений Q с соответствующими, распределениями вероятносте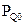й и 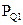, а f - произвольная функция отображения , преобразующая множество наблюдений Q во множество наблюдений 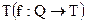. Тогда справедливо следующее выражение:

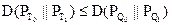
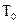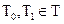где через и Соответственно помечены случайные величины 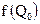и 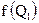Таким образом,

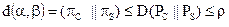
Учитывая что

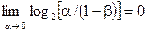
получаем

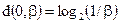
Следовательно, если 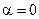, то 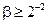. Теорема доказана

Итак, для 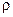-надежной стеганосистемы с 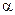= 0, необходимо обеспечить, чтобы 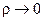. При этом вероятность 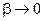, что эквивалентно невозможности выявления нарушителем скрытого в контейнере сообщения.