Динамические модели надежности

3.1.1. Модель Шумана

Исходными данными для модели Шумана, которая относится к динамическим моделям дискретного времени, собираются в процессе тестирования АСОД в течение фиксированных или случайных временных интервалов. Каждый энтервал - это стадия, на котором выполняется последовательность тестов и фиксируется некоторое число ошибок.

Модель Шумана может быть использована при определенном образе организованной процедуре тестирования. Использование модели Шумана предполагает, что тестирование поводиться в несколько этапов. Каждый этап представляет собой выполнение на полном комплексе разработанных тестовых данных. Выявление ошибки регистрируется, но не исправляются. По завершении этапа на основе собранных данных о поведении ПО на очередном этапе тестирования может быть использована модель Шумана для расчета количественных показателей надежности. При использовании модели Шумана предполагается, что исходное количество ошибок в программе постоянно, и в процессе тестирования может уменьшаться по мере того, как ошибки выявляются и исправляются.

Предполагается, что до начала тестирования в ПО имеется E_t ошибок. В течении времени тестирования t1 в системе обнаруживается E_c ошибок в расчете на команду в машинном языке.

Таким образом, удельное число ошибок на одну машинную команду, оставшуюся в системе после t1 времени тестирования, равно:

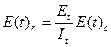(3.1)

где I_t – общее число машинных команд, которое предполагается в рамках этапа тестирования.

Предполагаем, что значение функции частоты отказов Z(t) пропорционально числу ошибок, оставшихся в ПП после израсходованного на тестирование времени t.

(3.2)

где С- некоторая константа,

t – время работы ПП без отказа, ч.

Тогда, если время работы ПП без отказа t отсчитывается от точки t = 0, а t1 остается фиксированным, функция надежности, или вероятность безотказной работы на интервале времени от 0 до t, равна:

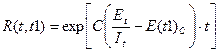(3.3)

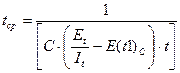(3.4)

Из величин, входящих в формулы (4.2) и (4.3) ,не известны начальное значение ошибок в ПП (E_t) и коэффициент пропорциональности – С. Для их определения прибегают к следующим рассуждениям. В процессе тестирования собирается информация о времени и количестве ошибок на каждом прогоне, т.е общее время тестирования t1 складывается из времени каждого прогона:

t1 = t₁ + t₂ + t₃ + …. + t_n (3.5)

Предполагая, что интенсивность появления ошибок постоянна и равна 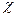, можно вычислить её как число ошибок в единицу времени:

где А_i – количество ошибок на i-м прогоне.

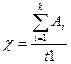(3.6)

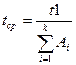
Имея данные для двух различных моментов тестирования t_A и t_b , которые выбираются произвольно с учетом требования, чтобы E_c(t_b) > E_c(t_A), можно сопоставить уравнения (3.4) и (3.6) при t_A и t_b :

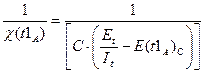(3.7)

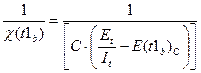(3.8)

Вычисляя отношения (3.7) и (3.8), получим

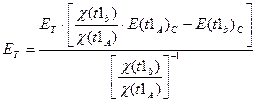(3.9)

Подставив полученную оценку параметров E_t в выражение (3.7), получим оценку для второго неизвестного параметра:

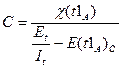(3.10)

Получив неизвестные Е_t и С, можно рассчитать надежность программы по формуле (3.3).

Достоинство этой модели заключается в том, что можно исправлять ошибки, внося изменения в текст программы в ходе тестирования, не разбивая процесс на этапы, чтобы удовлетворить требованию постоянства числа машинных инструкции.

3.1.2. Модель La Padula

По этой модели выполнение последовательности тестов производиться в m этапов. Каждый этап заканчивается внесением изменений (исправлений) в ПП. Возрастающая функция надёжности базируется на числе ошибок, обнаруженных в ходе каждого тестового прогона.

Надёжность ПП в течений i –го этапа:

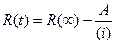(3.11)

где i = 1,2, … n,

А – параметр роста;

Предельная надежность ПП:

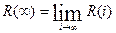(3.12)

Эти неизвестные величины можно найти, решив следующие уравнения:

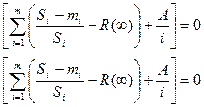(3.13)

где S_i – число тестов;

m_i – число отказов во время i-го этапа;

m – число этапов;

i = 1,2 … m.

Определяемый по этой модели показатель есть надежность АСОД на i-м этапе.

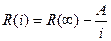(3.14)

где i = m+1,m+2 …

Преимущество данной модели заключается в том, что она является прогнозной и, основываясь на данных, полученных в ходе тестирования, дает возможность предсказать вероятность безотказной работы программы на последующих этапах её выполнения.