Методы экономии пространства для поиска по заданному критерию

12.4.1. Потребность алгоритма А* в ресурсах времени и пространства

Применение эвристических средств управления поиском по заданному критерию обычно позволяет сократить область поиска таким образом, чтобы в этом процессе посещались только узлы небольшой части: пространства состояний задачи. Такое уменьшение области поиска можно рассматривать как сокращение эффективного объема ветвления в процессе поиска. Таким образом, если "среднее" ветвление в про-

Глава 12. Эвристический поиск по заданному критерию

странстве состояний задачи равно Ь, то применение эвристических средств управле­ния поиском фактически приводит к возникновению среднего ветвления Ь', причем Ь' обычно значительно меньше чем Ь.

Несмотря на существенное уменьшение затрат на выполнение поиска, порядок сложности алгоритма А* (и его реализации, приведенной в листинге 12,1) продолжа­ет оставаться экспоненциально зависимым от глубины поиска. Такое утверждение остается справедливым в отношении потребности в ресурсах и времени, и простран­ства, поскольку данный алгоритм предусматривает необходимость сопровождения информации обо всех сформированных узлах в памяти. В практических приложени­ях наиболее важным может стать один из этих ресурсов (время или пространство), и это зависит от конкретных обстоятельств. Но в большинстве практических ситуаций более важным ресурсом является пространство. Алгоритм А* способен за считанные минуты израсходовать все доступное пространство памяти.А после этого поиск фак­тически не может продолжаться, притом что пользователи часто готовы ждать окон­чания работы этого алгоритма в течение многих часов или даже суток, поскольку для них весьма важны его результаты.

Разработано несколько вариантов алгоритма А*, позволяющих экономить про­странство за счет времени. По своему основному замыслу они аналогичны поиску в глубину с итеративным углублением (см. главу 11). Потребность в ресурсах про­странства сокращается от экспоненциальной до линейной зависимости от глубины поиска. Но за это приходится платить тем, что в пространстве поиска повторно фор­мируются ранее сформированные узлы.

В следующих разделах рассматриваются два метода экономии пространства в контексте поиска по заданному критерию. Первый из них называется IDA* (Iterative Deepening A* - алгоритм А* с итеративным углублением), а второй упоминается под названием RBFS (Recursive Best-First Search - рекурсивный поиск по заданному критерию).

12.4.2. Метод IDA*

Метод IDA* (Iterative Deepening A* - алгоритм А* с итеративным углублением) аналогичен поиску в глубину с итеративным углублением, за исключением описан­ного ниже отличия. При итеративном углублении поиск в глубину осуществляется со все возрастающими пределами глубины. При каждой итерации поиск в глубину ог­раничивается текущим пределом глубины. Но в методе IDA* последовательный по­иск в глубину ограничивается текущим пределом значений оценок узлов (т.е. эври­стических f-значений узлов). Поэтому основной механизм поиска в методе IDA* также основан на поиске в глубину, при котором потребность в ресурсах пространст­ва является очень низкой. Метод ГОА*можно сформулировать с помощью приведен­ной ниже алгоритмической конструкции.

Bound :-f(StartNode); Repeat

выполнить поиск в глубину, начиная с уэла StartNode, с соблюдением условия,

что узел N развертывается, только если f(H) £ Bound;

if при этом поиске в глубину встречается целевой узел

thenсообщить о том, что "решение найдено",

Else

вычислить NewBound как минимум f-змачений узлов, достигнутых непосредственно после выхода за пределы Bound:

KewBound = r.ir.{f ■:;; I узел N, сгенерированный на этом этапе поиска, /(H) > Bound} Bound: - KewBound until "решение найдено"

В качестве иллюстрации работы этого алгоритма рассмотрим применение алго­ритма А* к задаче поиска маршрута (рис. 12.2, 6), при условии, что f(s) = 6, При этом метод IDA* действует следующим образом:

Часть II.Применение языка Prolog в области искусственного интеллекта

Bound = f(s) = 6

Выполнить поиск в глубину, ограниченный значением f S 6. На. этом этапе поиска

развертывается узел s, формируются узлы а к е и обнаруживается следующее:

f (а) =7 > Bound

f[e) = 9 > Bound

NewBound = min ( 7, 9} =7 Выполнить поиск в глубину, ограниченный значением f < 1, начиная с узла s. Узлами с f-значениями, непосредственно превышающими этот предал, являются b и е.

NewBound = min { f(b), f(e)} " min{ 8, 9) = 8 В последующем предел Bound изменяется следующим образом: 9 (f(e)), 10 (f(c)), 11 [tit)). Для каждого из этих значений выполняется поиск в глубину. При выполнении поиска в глубину со значением Bound =11 возникает ситуация "решение найдено",

Хотя этот пример предназначен только для иллюстрации работы метода IDA*, он оставляет впечатление, что реализованный в нем алгоритм является громоздким, по­скольку поиск в глубину повторяется несколько раз. Но при решении крупных задач поиска экономия пространства, достигаемая с помощью метода IDA*, может оказать­ся весьма значительной, тогда как издержки, связанные с повторением поиска, ос­таются вполне приемлемыми. Величина этих издержек зависит от свойств простран­ства поиска, в частности от свойств функции оценки £. В благоприятных ситуациях многие узлы имеют равные f-значения. В подобных ситуациях на каждом очередном этапе поиска в глубину рассматривается много новых узлов, количество которых превышает количество повторно формируемых узлов. Поэтому дополнительные из­держки сравнительно малы, В неблагоприятных ситуациях f-значения, как правило, не являются одинаковыми для многих узлов. В крайнем случае каждый узел может иметь отличное от других f-значение. При этом возникает необходимость использо­вать целый ряд последовательных f-пределов, когда при каждом новом поиске в глу­бину формируется только один новый узел, а все остальные узлы представляют собой повторно сформированные узлы (которые были сформированы на предыдущих эта­пах и удалены из памяти), В таких крайних случаях дополнительные издержки, связанные с использованием метода IDA*, действительно становятся неприемлемыми.

Еще одно интересное свойство метода IDA* касается допустимости. Предположим, что функция f(8) определена как g (N) + h(N) для всех узлов И. Бели функция h является допустимой (т.е. h{N) < h* (N) для всех К), то метод IDA* гарантирует на­хождение оптимального решения.

Одним из возможных недостатков метода IDA* является то, что он не обеспечива­ет исследование узлов в порядке оценок по заданному критерию {т.е. в порядке воз­растания f-значений). Например, предположим, что £ — это функция оценки, кото­рая не обязательно представлена в форме f = g + h. Если функция f не монотонна, то упорядочение по заданному критерию не гарантируется. Функция f называется монотонной, если ее значение монотонно возрастает вдоль путей в пространстве со­стояний. Иными словами, f является монотонной, если для всех пар узлов И и N' справедливо утверждение: если s ( N, Н'), то £ (К) S £ (И '}. Причина нарушения упорядоченности по заданному критерию состоит в том, что при использовании не­монотонной функции f значение f-предела может стать настолько большим, что узлы с разными f-значениями будут впервые развертываться при этом поиске в глубину. Процедура поиска в глубину будет развертывать узлы до тех пор, пока для них зна­чение функции f не превысит f-предела, без учета того, в каком порядке они развер­тываются. В принципе мы заинтересованы в соблюдении упорядоченности по заданно­му критерию, поскольку надеемся на то, что функция f отражает качество решений.

Один из простых способов реализации метода IDA* на языке Prolog показан в листинге 12.4. В этой программе широко применяется механизм перебора с возвра­тами Prolog. Значение f-предела сопровождается как факт в форме next_bound( Bound)

который обновляется с помощью предикатов assert и retract. При каждой итера­ции предел для поиска в глубину определяется из этого факта. Затем (в результате

Глава 12. Эвристический поиск по заданному критерию

применения предикатов retract и assert к этому факту) предел для следующей итерации инициализируется значением 99999. Предполагается, что эта большая ве­личина превышает любое возможное f-значение. Поиск в глубину реализован в программе таким образом, что развертывание узла N допускается, только если fК] < Bound. Если же, с другой стороны, f (N) > Bound, то значение f(K) срав­нивается со значением Next Bound (которое хранится в виде факта next_bound(NextBound)). Если f (N) < NextBound, то факт nextjbound обновляет­ся для сохранения в нем значения f (Ы).

Упражнения

12.6. Сформируйте пространство состояний и функцию £, при использовании которых метод IDA* не развертывает узлы в порядке соблюдения заданного критерия.

12.7. Примените программу IDA*, приведенную в листинге 12.4, к головоломке "игра в восемь" с использованием определений отношения выбора преемника з/З и отношения totdist/З, показанных в листинге 12.2. В качестве эври­стической функции h (для обеспечения допустимости) применяйте только суммарное расстояние (totdist/З). Определите также предикат f/2 (необхо­димый для программы IDA*) таким образом, чтобы f {N) = д (и) + Ъ.(Ы).Для обеспечения возможности вычисления g(N) храните g-значение узла явно в составе представления этого узла (например, Ш = GrTilePosltions). Прове­дите эксперименты с головоломкой "игра в восемь", которая определена в лис­тинге 12.2. Попробуйте также применить начальное состояние

[1/2,3/3,3/1,1/3,3/2,1/1,2/3, 2/1,2/2]. Сравните значения времени выполнения и длины пути решения, найденные с помощью алгоритма А* (с использованием эвристической функции листинга 12.2) и метода IDA* {с использованием только суммарного расстояния).

Листинг 12.4. Реализация алгоритма ЮА*

* idastar{ Start, Solution):

% выполнение поиска по алгоритму IDA*,- Start - это начальный узел, % Solution - путь решения

% Удалить из базы данных значение Ь следующего предела I Инициализировать значение предела

idastari Start, Solution) :-retract!. next_bourid <_J |, fail

assertat next_bound ( 0)) , idastarO< Start, Solution).

idastarO[ Start, Sol) :-

i Текущий предел % Инициализировать значение следующего предела % f-значение начального узла % Найти решение; в случае неудачи % изменить значение предела % Значение предела является конечным % Предпринять попытку с новым значением предела

retract( nextjbound( Bound)), asserta{ nextjbound( 99999)), f[ Start, F!, df( [Start], F, Bound, Sol)

nextjaoundt NextBound;, MextBound < Э93ЭЭ, idastarOt Start, Sol) .

I df( Path, F, Bound, Sol): % выполнить поиск в глубину в пределах Bound. Здесь Path - путь от начального % до текущего узла (представленный в виде списка узлов в обратном порядке), I F представляет собой f-значение текущего узла, т.е. головы списка Path

df( [И l Ns!, F, Bound, [ТЛ | Ball :-
F =< Bound,
goal! N) . % Успешное завершение - решение найдено

Часть II. Применение языка Prolog в области искусственного интеллекта

f-эначение узла N не выходит за пределы Развернуть N

df( [Ml S3], F, Bound, Sol) :-F -< Bound,

s( N, HI) , not member ( HI, Ns), 1 f( N1, Fl) , df( [N1,NI He], Fl, Bound, Sol).

% За пределами Bound % Только обновить следующее значение предела и инициировать неудачное завершение

df( _, F, Bound, _) :-F > Bound, updatenextbound[ F),

fail.

update_next_boimd ( F) : -next_bound( Bound},

Bound =< F, ]

retract( next_bound( Bound)), !, assertat next bound( F)}.

изменять следующее значение предела % Более низкое следующее значение предела

12.4.3. Метод RBFS

Метод IDA* основан на продуктивной идее и является очень удобным для реали­зации, но в неблагоприятных ситуациях связанные с ним издержки повторного фор­мирования узлов становятся неприемлемыми. Поэтому применяется лучший, хотя и более сложный метод экономии пространства, получивший название RBFS (Recursive Best-First Search - рекурсивный поиск по заданному критерию). Реализация метода RBFS весьма напоминает программу А*, приведенную в листинге 12.1 (которая так­же является рекурсивной, в том же смысле, что и RBFS!). Различие между програм­мами А* и RBFS состоит в том, что первая обеспечивает хранение в памяти всех ра­нее сформированных узлов, а последняя предусматривает хранение только текущего пути поиска одноранговых узлов вдоль этого пути. Если программа RBFS на время приостанавливает поиск в поддереве (поскольку оно больше не соответствует задан­ному критерию), то удаляет из памяти это поддерево для экономии пространства. Поэтому потребность в ресурсах пространства для программы RBFS (как и при ис­пользовании метода IDA*) зависит от глубины поиска только линейно. При исполь­зовании метода RBFS единственное, что сохраняется в памяти об удаленном поддере­ве, - обновленное f-значение для корня этого поддерева. Такие f-значения обновля­ются по методу сопровождения резервных копий f-значеняй таким же образом, как и в программе А* Чтобы подчеркнуть различия между "статической" функцией оценки f и резервными копиями ее значений, используются приведенные ниже фор­маты записей (для узла К),

• f {N). Значение узла;:, возвращенное функцией оценки (всегда остается одним и тем же во время поиска).

• F(N). Резервная копия f-значения (изменяется во время поиска, поскольку за­висит от узлов-потомков узла N).

Значение F(N) определяется следующим образом.

• F(N> = f(N), если узел N (никогда) не развертывался в процессе поиска.

• F(N} = min{ FfNi) | Ni - дочерний узел узла N) в противном случае.

Как и программа А*, программа RBFS также предусматривает исследование под­деревьев, соответствующих указанному f-пределу. Этот предел определяется по F-значениям одноуровневых узлов вдоль текущего пути поиска (по минимальному F-значению для одноуровневых узлов, т.е. по F-значению узла, который является ближайшим конкурентом текущего узла). Предположим, что узел N в настоящее время является наилучшим узлом в дереве поиска (т.е. имеет минимальное F-значение). В таком случае узел N развертывается и дочерние узлы узла N исследу­ются вплоть до некоторого f-предела Bound. При превышении этого предела (что об­наруживается с помощью выражения F [И) > Bound) все узлы, сформированные на

Глава 12.Эвристический поиск по заданному критерию

уровне ниже N, удаляются из памяти. Но обновленное значение F(U] сохраняется и используется при определении того, как продолжать поиск.

В программе F-значения могут быть не только определены путем создания ре­зервных копий значений, полученных от дочерних уалов рассматриваемого узла, но и унаследованы от родительских узлов этого узла. Такое наследование происходит следующим образом. Предположим, что имеется узел Н, для которого настало время быть развернутым в процессе поиска. Если F(N) > f (N) , то известно, что узел N уже был развернут ранее и значение F{N) определено с помощью дочерних узлов узла N, но эти дочерние узлы уже удалены из памяти. Теперь предположим, что дочерний узел Ni узла N снова сформирован и статическое значение f (Ni> для узла также снова вычислено. Теперь значение F(Ni) определяется следующим образом:

если f{Ni) <F(N), то F(M;) = F[N), иначе F(NiJ = fCN_;)

Это выражение может быть записано короче следующим образом: F[Hi)= raax{F(H), f (N,) }

Таким образом, в том случае, если f(N1) < С(Ы) , то F-значение узла К. фактиче­ски наследуется от родительского узла S узла Hi. Это можно показать с помощью следующих рассуждений: когда узел Ni был сформирован (и удален) ранее, значение F(Ni> обязательно было больше или равно F(N). В противном случае, согласно пра­вилу создания резервной копии, значение F(N) должно было быть меньше.

Для иллюстрации процесса функционирования программы RBPS рассмотрим за­дачу поиска маршрута (см. рис. 12.2). На рис. 12.7 приведены отдельные снимки те­кущего пути (включая одноуровневые узлы вдоль этого пути), хранящиеся в памяти. При поиске происходит переключение (как и в программе А*) между альтернатив­ными путями. Но после каждого такого переключения предыдущий путь удаляется из памяти для экономии пространства. На рис. 12.7 числа, стоящие рядом с узлами, представляют собой F-эначения этих узлов. На снимке А узел а является наилучшим из возможных узлов (F{a) < F{e}). Поэтому происходит поиск в поддереве ниже узла а со значением Bound = 9 (т.е. со значением, равным F(e); им характеризуется ближайший и единственный конкурент). После достижения в этом поиске узла с (снимок Б) обнаруживается, что F{c) » 10 > Bound. Поэтому поиск по этому пути (на время) прекращается, узлы с и Ь удаляются из памяти, значение F(c) = 10 со­храняется в виде резервной копии в узле а и значение F(a) становится равным 10 (снимок В). Теперь узел е становится наилучшим конкурентом (F(e) = 9 < 10 = F{a]) и происходит поиск в его поддереве со значением Bound = 10 = F(a). Этот поиск останавливается на узле f, поскольку F(f) = 11 > Bound (снимок Г). Узел е удаляется, и F(e) принимает значение 11 (снимок Д). Теперь поиск снова переклю­чается на узел а со значением Bound = 11. После повторного формирования узла Ь обнаруживается, что f (Ь) = 6 < F{a). Поэтому узел в наследует свое F-эначение от узла а таким образом, что F(b) становится равным 10. Затем повторно формируется узел с и также наследует свое F-значение от Ь, поэтому F(c) становится равным 10. Значение Bound = - 1 превышается на снимке Е, узлы d, с и Ь удаляются и в узле а сохраняется резервная копия значения F(d) = 12 (снимок Ж). Теперь поиск пере­ключается на узел е и беспрепятственно продолжается до цели t.

Ниже приведено более формальное определение алгоритма RBFS. В основе этого алгоритма лежит принцип обновления F-значений узлов. Поэтому удобный способ формулировки данного алгоритма состоит в определении следующей функции:

NewF( В, F(N), Bound)

где N — узел, текущее F-значение которого равно F (N). Функция выполняет поиск в пределах Bound, начиная с узла .:, и вычисляет новое F-значение узла N, NewF, полу­ченное в результате этого поиска. Новое значение определяется в момент превыше­ния предела. Но если цель удается найти еще до этого, то функция прекращает свою работу, сообщая об успехе как о побочном результате своей работы. Функция NewF определена в листинге 12.5.

270 Часть II. Применение языка Prolog в области искусственного интеллекта

А Б В

⁷0>0^{5 7}<jJ©^{9 10}© 0⁹

\	10©
г	д	В
А	А	JK,
10 0 ©9	10 0 ©И	»© ©"
4»		"|
щ		"Ф
А	А	1г0
12 0 011	12 © ©И

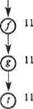
Рис. 12.7, Трассировка выполнения алгоритма RBFS в процессе решения задачи поиска маршрута, показанной на рис. 12.2; числа рядом с узлами представляют собой F-значения этих узлов (которые изменяются во время поиска)

Листинг 12.5. Функция обновления F-значенийв процессе поиска по методу RBFS

function Hewf( В, F(H), Bound) begin

if F(N)> Bound thenNewF ;= F(N)

else ifgoal(H) thenуспешное завершение процедуры поиска

else ifИ не имеет дочерних узлов thenNewF := infinity (тупиковый конец)

else

Begin

forкаждого узлаHi, дочернего по отношению к N doif f [HI< F!N} thenF!Nil :« max [ F(N) , f (Nil ) elseF(Hi) := f (Mi) ; сортировать дочерние узлы Ni в порядке возрастания их F-значений;while Г {Hi) S Bound andF ffli) < infinity dobegin

Boundl := min( Bound, F-значение наилучшего по сравнению с Hi однорангового узла);

Глава 12. Эвристический поиск по заданному критерию

F(Ni> := KewF( Hi [ F[H_t), Boundl); переупорядочить узлы Hi, Щ, ... в соответствии с нозым значением F(Ni) end NewF : = F(Ni) end end

Реализация алгоритма RBFS на языке Prolog приведена в листинге 12.6. Эта про­грамма аналогична программе А*, показанной в листинге 12Л, Основой этой про­граммы является процедура

rbfs! Path, SiblingNodes, Bound, NevmestFF, Solved, Solution) которая реализует алгоритм RBFS. Параметры этой процедуры описаны ниже.

• Path. Найденный к этому моменту путь от начального узла поиска, представ­ленный в виде списка узлов в обратном порядке.

• SiblingNodes. Дочерние узлы последнего узла в пути, пройденном до сих пор, т.е. голова списка Path.

• Bound. Верхний предел F-значений для развертывания пояска от узлов

SiblingNodes.

• MewBestFF. Наилучшее F-значение после развертывания поиска непосредст­
венно за пределы Bound.

■ Solved. Индикатор успеха поиска на уровне ниже узлов SiblingNodes (Solved = yes, если цель найдена, Solved = no, если поиск только что вы­шел за пределы Bound, и Solved = never, если это направление является бесперспективным, или тупиковым).

• Solution. Путь решения, если Solved - yes, в противном случае — некон-
кретизированная переменная.

Представления узлов, кроме состояния в пространстве состояний, включают так­же стоимости пути, f- и F-значения, как показано ниже. Node = ( State, G/F/FF)

где G — стоимость пути от начального состояния до состояния State, F — статиче­ское значение, f (State}, a FF - текущее значение резервной копии W(StateСле­дует отметить, что переменная F в этой программе обозначает f-значение, a FF -F-значение. Процедура rbfs выполняет поиск на уровне ниже узлов SiblingNodes в пределах Bound и вычисляет значение NewBestFF в соответствии с функцией NewF, показанной в листинге 12.5.

Листинг 12.6. Программа поиска по заданному критерию, для которой потребность в пространстве линейно зависит от глубины поиска (алгоритм RBFS)

% Программа поиска по заданному критерию, для которой потребность в пространстве

% линейно зависит от глуоины поиска, - алгоритм RBFS. В этой программе

% предполагается, что f-значение ни при какихусловиях не превышает 99999

Чbestfirst( Start, Solution): где Solution - путь от начального узла Start Ч до целевого узла

bestfirstf Start, Solution) :-

rbfsl ['] , ( (Start, 0/0/0) ], 99999, _, yes, Solution).

% rbfs ( Path, SiblingNcdes, Bound, NewBestFF, Solved, Solution) :

1 Path - текущий путь, представленный в виде списка узлов в обратном порядке

I SiblingNodes - дочерние узлы узла в голове списка Path

Ч Bound - верхняя граница F-эначения для поиска по узлам списка sibiingModes

Часть II.Применение языка Prolog e области искусственного интеллекта

% NewBestFF - наилучшее f-эначение после поиска, непосредственно
% за пределами Bound

% Solved - yes, no :■:,-;: never

1 Solution - путь решения, если Solved = yes

% Представление узлов: Node - ( State, G/F/FF)

4 где G - стоимость до наступления состояния State, F - статическое £-значеиие

% в состоянии State, FF - резервная копия 1-значения в состоянии State

rbfst Path, [ -{Node, G/F/FF) I Modes], Bound, FF, no, _) :-FF > Bound, ! .

rbfs{ Path, [ [ Node, G/F/FF) ] , _, _, yes, [Node I Path]) :-

F = FF, % Сообщать об успешном решении только один раз, после первого

% достижения целевого узла,- затем F=FF goalt Node).

rbfst _, [],_,_, never, _) :- !. i Возможные продолжения отсутствуют,

% тупиковый конец!

rbfs( Path, ( ( Node, G/F/FF) I Ns ] , Bound, NewFF, Solved, Sol) :-

FF =< Bound, i Значение в пределах Bound - сформировать дочерние узлы

findall [ Child/Cost,

[s. Node, Child, Cost), not member [ Child, Path)),
Children),
inherit{ F, FF, InheritedFF) , % Дочерние узлы могут наследовать значение FF
succlist( G, InheritedFF, Children, SuccNodes), % Переупорядочить эти узлы
bestfft Ns, NextBeStFF) , % Ближайший конкурент г.о значению FF среди

% одноранговых узлов min[ Bound, NextBestFF, Bound2), I,

rbfst [Node I Path], SuccNodes, Bound2, NewFF2, Solved2, Sol), continue (Path, [ (Node, G/F/NewFF2 > INs ] , Bound, NewFF, Solved'2, Solved, Sol).

I continue) Path, Nodes, Sound, NewFF, ChildSolved, Solved, Solution)

continue! Path, [N I Ns], Bound, NewFF, never. Solved, Sol) :- !,

rbfs( Path, Ns, Bound, NewFF, Solved, Sol) . % Узел N - это тупиковый конец

continue! _, _, _, _, yes, yes, Sol) .

continue С Path, ( N I Ns], Bound, NewFF, no. Solved, Sol) :-

insert,- N, Ns, NewNs), !, % Соблюдать упорядочение одноранговых узлов

% по значениям rbfs{ Path, NewNs, Bound, NewFF, Solved, Sol) .

succlist ( _, _, [] , [] ) .

SuCCliSttGO, InheritedFF, [Node/C I NCsJ, Nodes) :-G is GO + С h( Node, H) , F is G + H,

max ( F, InheritedFF, FF) ,

succlistt GO, InheritedFF, NCs, Nodes2>,

insert; ( Node, G/F/FF), Nodes2, Nodes).

inheritf F, FF, FF) :- % Дочерний узел наследует FF-ЭНЭЧение родительского
FF > F, !. Ъ узла, если FF-значение родительского узла больше

% F-значения родительского узла

inherit,- F, FF, 0) .

insert,- ( N, G/F/FF), Nodes, I ( N, G/F/FF) | Nodes]) :-bestff( Nodes, FF2), FF =< FF2, !.

Глава 12.Эвристический поиск позаданному критерию 273

insert) N, till I Ms), (Ml I NslJ) :-insert ( N, Ms, Nsl) .

bestffl [ ( H, F/G/FF) 1 Ms], FF) . % Первый узел - наилучшее FF-значение

bestff ( [], 99999). I Узлы отсутствуют - FF-эначение равно

% "бесконечно большому числу"

Еще раз кратко опишем наиболее важные свойства алгоритма RBFS. Во-первых, он характеризуется тем, что потребность в ресурсах пространства зависит от глубины поиска линейно. За это приходится платить увеличением затрат времени на повтор­ное формирование ранее сформированных, узлов. Но эти издержки значительно ниже по сравнению с алгоритмом IDA*. Во-вторых, аналогично А* и в отличие от IDA*, в алгоритме RBFS предусмотрено развертывание узлов с упорядочением по заданному критерию даже а случае немонотонной функции ;.

Упражнения

12.8.Рассмотрим задачу поиска маршрута, показанную на рис. 12.2. Сколько узлов формируется при решении этой задачи с помощью алгоритмов A*, IDA* и RBFS {с учетом также повторно формируемых узлов)?

12.9.Рассмотрим пространство состояний, показанное на рис. 12.8. Допустим, что а - начальный узел, 1 - целевой узел. Укажите порядок, в котором форми­ровались узлы (включая случаи повторного формирования) с помощью алго­ритма RBFS. Как изменялись резервные копии значений F(b) и F(c) а тече­ние этого процесса?

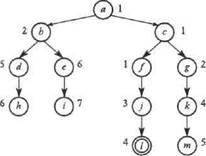Рис. 12.8. Пространство состояний; числа рядом с узлами представляют собой f-значения узлов; 1 — целевой

узел

12.10.Наследование F-значений в алгоритме RBFS позволяет сэкономить время (исключить ненужное повторное формирование узлов). Объясните, почему. Подсказка: рассмотрите процесс поиска по алгоритму RBFS в бинарном дереве, в котором f-значение каждого узла равно глубине этого узла в дереве. Проана­лизируйте, как происходит выполнение алгоритма RBFS с наследованием и без наследования F-значений в этом пространстве состояний вплоть до глубины 8.

12.11.Сравните программы A*, IDA* и RBFS для решения задач с различными усло­виями головоломки "игра в восемь". Измерьте значения времени выполнения и определите количество узлов, формируемых во время поиска, включая по­вторно формируемые узлы (введите в программы счетчики узлов).

Часть II. Применение языка Prolog в области искусственного интеллекта

Резюме

• Эвристическая информация может использоваться для оценки того, насколько далеко находится некоторый узел от ближайшего целевого узла в пространстве состояний. В этой главе рассматривалось применение числовых эвристических оценок.

• Принцип эвристического поиска по заданному критерию позволяет направ­лять процесс поиска таким образом, чтобы всегда развертывался тот узел, ко­торый в настоящее время является наиболее перспективным согласно эвристи­ческим оценкам. В данной главе приведена программа реализации широко из­вестного алгоритма А*, в котором используется этот принцип.

• Для того чтобы можно было воспользоваться алгоритмом А* при решении
конкретной задачи, необходимо определить пространство состояний, целевой
предикат и эвристическую функцию. При решении сложных задач труднее
всего найти приемлемую эвристическую функцию.

■ Теорема допустимости позволяет определить, всегда ли алгоритм А*, в кото­ром используется конкретная эвристическая функция, находит оптимальное решение.

• Потребности алгоритма А* в ресурсах времени и пространства обычно нахо­дятся в экспоненциальной зависимости от длины решения. В практических приложениях ресурсы пространства чаще всего являются более важными, чем ресурсы времени. Для экономии пространства за счет времени предназначены специальные методы поиска по заданному критерию.

• IDA* — это простой алгоритм поиска по заданному критерию, обеспечиваю­щий экономию пространства, который основан на идее, аналогичной итератив­ному углублению. Издержки, связанные с повторным формированием узлов при использовании алгоритма IDA*, являются приемлемыми в тех случаях, если многие узлы в пространстве состояний имеют одинаковые f-значения, А если узлы, как правило, не имеют одинаковых f-значений, издержки стано­вятся неприемлемыми.

• RBFS — это более сложный алгоритм поиска по заданному критерию, способ­ствующий экономии пространства, который обычно требует повторного фор­мирования меньшего количества узлов, чем IDA*.

• Требования к пространству алгоритмов IDA* и RBFS являются весьма умерен­ными. Они возрастают с глубиной поиска лишь линейно.

• В этой главе поиск по заданному критерию применялся в задаче решения го­ловоломки "игра в восемь" и в задаче планирования заданий.

• В данной главе рассматривались следующие понятия:

• эвристические оценки;

• эвристический поиск;

• поиск по заданному критерию;

• алгоритмы^*, IDA*, RBFS;

• допустимость алгоритмов поиска, теоремы допустимости;

• пространственная эффективность поиска по заданному критерию;

• монотонность функции оценки.