Методы структурного и временного резервирования

Основным параметром структурного резервирования является кратность, представляющая собой отношение числа резервных и основных элементов:

M=m/k, где m - число резервных подсистем, k - основных подсистем в резервной группе. Подсистемой в данном случае называется совокупность основных или резервных элементов, подлежащих замене при отказе хотя бы одного элемента этой совокупности (т.е. элементы соединены последовательно).

При k=1 кратность резервирования называют целой, при k<1 - дробной.

При резервировании с целой кратностью система является последовательным соединением n резервных групп, каждая из которых имеет структуру (параллельное соединение). В состав i-й группы входят один основной и m_i резервных элементов. Все элементы одной группы одинаковы и имеют одну и ту же функцию распределения наработки до отказа F_i(t). Вероятность безотказной работы системы: .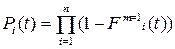

При резервировании с дробной кратностью количество резервных единиц меньше числа основных элементов. Это возможно, например, когда все элементы системы одинаковы. Резервные элементы не закрепляются за определенными основными элементами, а могут заменить любой из них. При выходе из строя одного рабочего элемента вместо него включается один резервный элемент. (Скользящее резервирование). Резервированная система состоит из l отдельных систем. Для ее нормальной работы необходимо, чтобы исправными были не менее, чем h систем. Кратность: l-h/h. Расчетные формулы для основных количественных характеристик надежности, таким образом, резервированной системы могут быть получены при следующих допущениях:

1)отказы элементов удовлетворяют условиям простейшего потока отказов;

2) переключающие устройства идеальны;

3) основные и все резервные системы равнонадежны.

Т.е все резервные системы находятся в рабочем состоянии с момента включения резервированной системы в работы. При отказе одной или всех l-h систем режимы работы оставшихся не меняются. Резервированная таким образом система будет работать нормально при следующих возможных ситуациях:

- ни одна из систем не отказала;

- отказала одна система;

- отказали две системы

….

- отказали l-h систем.

Тогда вероятность безотказной работы системы равна: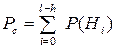

Где H_i - гипотеза, заключающаяся в том, что резервированная систем будет исправно работать при отказе i любых систем; P(H_i) - вероятность появления гипотезы H_i. Так как отказы элементов являются событиями независимыми и происходящими при одинаковых условиях работы отдельных систем, то применима теорема о повторении опытов, а вероятности гипотез подчинены биноминальному распределению:

,

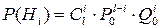где P_o и Q_o - вероятность безотказной работы и вероятность отказа одной системы. Биномиальные коэффициенты: 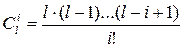И соответственно: .

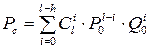Так как 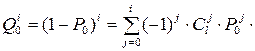, то

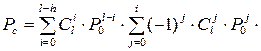
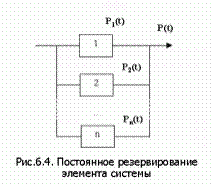
2.1. Постоянное (нагруженное, "горячее") резервирование элементов систем

При постоянном резервировании (рис.) резервные элементы постоянно присоединены к основному и функционируют одновременно, начиная с момента включения системы. Т.е. резервные элементы с самого начала работы системы подвергаются опасности отказа. Такая структура предполагает параллельное включение элементов с использованием формулы умножения вероятностей независимых в совокупности случайных событий, вероятность отказа системы в рассматриваемый момент времени t составит: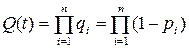

Вероятность безотказной работы системы: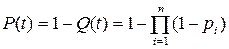

Достоинство - простота и экономичность, недостаток - изменение электрических режимов остальных элементов при отказе данного. Можно показать, что при малых наработках указанный способ обеспечивает увеличение вероятности безотказной работы.

2.2. Резервирование замещением (ненагруженное, динамическое, "холодное")

При резервировании замещением резервные элементы находятся в отключенном состоянии и не подвергаются опасности отказа до момента включения, наступающего при отказе основного (предшествующего резервного) элемента. Замещение отказавшего основного элемента резервным можно проводить вручную, полуавтоматически и автоматически. В первом случае никакой аппаратуры переключения не требуется, но время переключения довольно велико. При автоматическом переключении используется специальный автомат переключения резерва. Он уменьшает время переключения, однако сам обладает конечной надежностью.

Сравнение показывает, что резервирование замещением является более эффективным способом повышения безотказности элементов систем, чем постоянное резервирование, причем относительное увеличение вероятности безотказной работы особенно велико при больших значениях наработки.

Вычислим вероятность безотказной работы при следующих допущениях:

1) все резервные системы до момента замещения равнонадежны;

2) переключающие устройства в смысле надежности идеальны;

3) ремонт резервированной системы в процессе ее работы невозможен.

Пусть первоначально резервированная система состоит из одной рабочей А и одной резервной систем Б. При принятых допущениях отказ системы будет присутствовать при следующих возможных событиях:

А) система А в течение времени t не отказала;

Б) система А отказала в момент времени t, а система Б, будучи исправной до момента замещения t, оставалась исправной в течении времени (t-t).

Тогда вероятность безотказной работы резервированной системы в течение времени t: P_c(t)=P_A(t)+P_Б/А(t,t).

P_A(t) - вероятность безотказной работы системы А в течении времени t;

P_Б/А(t,t) - вероятность безотказной работы системы Б в течение времени t при условии, что отказ системы А произошел в момент времени t, которая равна:

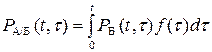. Тогда вероятность безотказной работы резервированной системы равна: 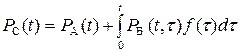. Резервные системы теряют надежность лишь с момента замещения отказавшей системы ("холодный резерв"), т.е. ее отказ до момента t произойти не может, поэтому P(t,t)= P(t-t). Для системы с кратностью резервирования m при равной вероятности P(t) резервных и замещаемого элементов можно получить: 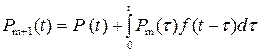. Это реккурентная формула. На практике часто встречаются задачи, когда требуется по известной вероятности безотказной работы нерезервированной системы вычислить вероятность безотказной работы резервированной m раз. Для решения этой задачи по формуле необходимо первоначально вычислить вероятность безотказной работы при m=1, затем по полученному результату вычислить P(t) при m=2 и т.д.