Пример вероятностного расчета на основе случайного графа
Задача 1.
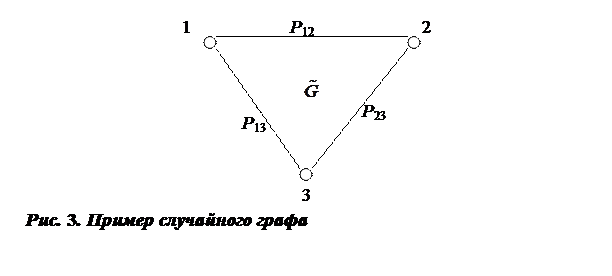
Пусть задан случайный граф 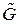 , изображенный на рис. 3, и требуется определить вероятность связности вершин 1 и 2
, изображенный на рис. 3, и требуется определить вероятность связности вершин 1 и 2 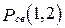 .
.
Существует несколько путей решения этой задачи.
Путь 1.
Сначала рассмотрим все возможные пути из вершины 1 в 2. Всего их два: 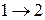 ;
; 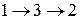 .
.
Вероятность существования первого пути 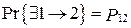 , второго –
, второго – 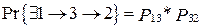 . Следовательно, вершины 1 и 2 связны с вероятностью
. Следовательно, вершины 1 и 2 связны с вероятностью
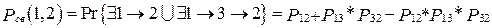 (1)
(1) 
Путь 2.
Рассмотрим множество 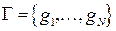 всех возможных неслучайных графов, которые можно получить на основе случайного. Каждый такой граф
всех возможных неслучайных графов, которые можно получить на основе случайного. Каждый такой граф 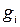 может появиться со своей вероятностью
может появиться со своей вероятностью 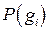 . Среди них выделим подмножество
. Среди них выделим подмножество 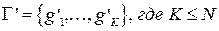 , в котором путь из вершины 1 в вершину 2 существует. Для рассматриваемого примера N = 8, К = 5. Список элементов
, в котором путь из вершины 1 в вершину 2 существует. Для рассматриваемого примера N = 8, К = 5. Список элементов 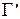 и вероятности появления такого графа представлены в таблице 1.
и вероятности появления такого графа представлены в таблице 1.
| N | Ребро 1-2 | Ребро 2-3 | Ребро 1-3 | Вероятность появления 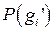 |
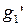 | нет | есть | есть | 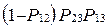 |
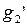 | есть | нет | нет | 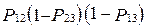 |
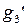 | есть | нет | есть | 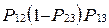 |
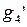 | есть | есть | нет | 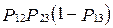 |
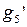 | есть | есть | есть | 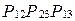 |
Теперь просуммируем вероятности, соответствующие элементам множества 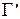 , и получим окончательный ответ, совпадающий с результатом формулы (1):
, и получим окончательный ответ, совпадающий с результатом формулы (1):
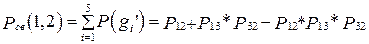
Путь 3.
Рассмотрим две ситуации. Для первой будем полагать, что ребро 2-3 всегда существует. Для второй ситуации будем полагать, что ребро 2-3 не существует. В этом случае можно перейти к рассмотрению двух новых случайных графов: 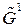 , появление которого возможно с вероятностью
, появление которого возможно с вероятностью 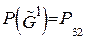 , и
, и 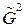 , который может появиться с вероятностью
, который может появиться с вероятностью 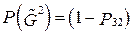 , как это показано на рис. 4.
, как это показано на рис. 4.

Поскольку ребро 2-3 для случайного графа 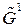 существует всегда, то вершины 2 и 3 можно объединить в одну, как показано на рис. 3. Для
существует всегда, то вершины 2 и 3 можно объединить в одну, как показано на рис. 3. Для 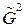 же ребро 2-3 просто отсутствует.
же ребро 2-3 просто отсутствует.
Такую процедуру получения более простых случайных графов на основе одного сложного будем называть декомпозицией.
Для полученных с помощью декомпозиции случайных графов определим вероятность связности вершин 1 и 2:
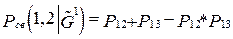 (2)
(2)
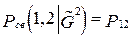 (3)
(3)
Теперь, чтобы получить вероятность связности для случайного графа 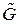 воспользуемся формулами (2) и (3):
воспользуемся формулами (2) и (3):
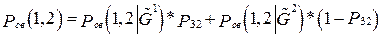 (4)
(4)
Нетрудно проверить, что результаты формул (1) и (4) совпадают.
Декомпозицию для новых графов можно продолжать. При этом в узлы построенного таким образом «двоичного дерева» будут отображаться случайные графы. Существенно то, что случайные графы, находящиеся на нижних ярусах, будут иметь более простую топологию по сравнению с графами на вышестоящих ярусах.
Основная цель процедуры декомпозиции состоит в замене одного сложного графа на несколько простых, для которых проще произвести расчет вероятности связности.
