Условные обозначения блоков схем алгоритмов

Наименование	0бозначенне	Функции
Процесс		Выполнение операции или группы операции, в результате которых изменяется значение, форма представления или расположение данных.
Ввод-вывод		Преобразование данных в форму, пригодную для обработки (ввод) или отображения результатов обработки (вывод).
Решение		Выбор направления выполнения алгоритма в зависимости от некоторых переменных условии.
Предопределенный процесс		Использование ранее созданных и отдельно написанных программ (подпрограмм).
Документ		Вывод данных на бумажный носитель.
Магнитный диск		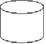Ввод-вывод данных, носителем которых служит магнитный диск.
Пуск-останов		Начало, конец, прерывание процесса обработки данных.
Соединитель		Указание связи между прерванными линиями, соединяющими блоки.
Межстраничный соединитель		Указание связи между прерванными линиями, соединяющими блоки, расположенные на разных листах.
Комментарий		Связь между элементом схемы и пояснением.

Ход работы и задания:

Составить алгоритм решения следующих задач двумя способами: словесно-формульным и с помощью блок-схемы:

1. Дана длина ребра куба. Составить алгоритм нахождения площади грани, площади полной поверхности и объема этого куба.

2. Составьте алгоритм для нахождения расстояния между пешеходами, идущими навстречу друг другу, начавшими путь одновременно.

L₀ - начальное расстояние,

V₁ - скорость первого пешехода,

V₂ - скорость второго пешехода,

T - время движения,

L₁ - текущее расстояние.

3. Составьте алгоритм нахождения максимального числа из двух заданных.

4. Написать алгоритм, имитирующий работу микрокалькулятора (выполнение 4-х арифметических действий).

5. Составьте алгоритм нахождения площади треугольников, заданных сторонами a, b, (c+k), где k=1,2,...,15.

6. Составьте алгоритм вычисления S=m(m+1)(m+2)...(m+n), где m, n- заданные натуральные числа.

Контрольные вопросы и задания:

1) Перечислите способы составления алгоритмов.

2) Алгоритмы какой структуры вы знаете?

3) Какую структуру имеет алгоритм, составленный с помощью словесного способа?

4) Какую структуру имеет линейный алгоритм, составленный с помощью блок-схемы?

5) Какую структуру имеет алгоритм ветвления, составленный с помощью блок-схемы?

Рекомендуемая литература: 1.3, 1.4, 1.5.

Практическое занятие №2 " Применение машины Тьюринга к словам "

Цель: Закрепить знания применения машин Тьюринга к словам.

Вид работы: фронтальный.

Время выполнения: 4 часа.

Теоретический материал:

Машина Тьюринга состоит из следующих частей:

1. Информационной ленты, представляющей бесконечную память машины. Это бесконечная лента, разделенная на ячейки. В каждой ячейке можно поместить лишь один символ из возможного их множества S={S₁,S₂,….,S_m},которое составляет внешний алфавит МТ. В этом алфавите один из символов (пусть это будет S₁) соответствует пустому символу.

2. Считывающей головки – чувствительного специального элемента, способного обозревать содержимое ячеек. Лента может перемещаться вдоль головки так, что в каждый момент времени головка обозревает одну ячейку.

3. Управляющего устройства (УУ), которое в каждый момент времени находится в некотором состоянии. Число состояний конечно. Обозначим множество состояний как {q₁,q₂,…,q_n}. Среди состояний одно соответствует заключительному, при котором МТ останавливается. УУ связано со считывающей головкой.

Кроме того, УУ вырабатывает три команды на перемещение ленты: П, Л, Н, где

П – переместиться на соседнюю справа ячейку;

Л – переместиться соседнюю слева ячейку;

Н – продолжать обозревать ту же ячейку.

Совокупность символов {q₁,q₂,…,q_n} и {П,Л,Н} образуют внутренний алфавит МТ.

Работа машины происходит в дискретном времени. В начальный момент времени в ограниченный участок ленты записано слово в алфавите S, представляющее исходное условие задачи. В остальных ячейках предполагается записанным пустой символ. Управляющее устройство находится в начальном состоянии q₁. На каждом шаге работы МТ обозревает на ленте символ S_k и в зависимости от него и от состояния q_i, переходит в состояние q_j, заменяет S_k на символ S_l и передвигает ленту (либо нет) на одну ячейку.

Каждая элементарная операция имеет вид

q_iS_k ® q_jS_l П(Л,Н).

Множество элементарных операций упорядочено и образует абстрактную программу, которая представляет алгоритм.

Считывающая головка и управляющее устройство образуют логический блок, который представляет собой (2,3)-полюсник.

Структура МТ имеет следующий вид:

S1

S2

…

Sk

…

Sm

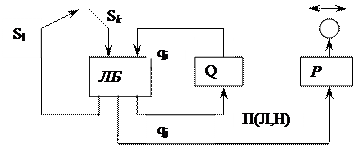
Q - ячейка хранит символ состояния, а Р - ячейка – символ сдвига. В них происходит задержка данных символов до начала следующего такта.

В качестве начальной информации на ленту можно записать любую конечную последовательность символов (входное слово) U внешнего алфавита. В начале работы алгоритма устройство управления находится в начальном состоянии, головка обозревает первый слева непустой символ входного слова U. Если после конечного числа тактов МТ останавливается, переходя в заключительное состояние, а на ленте оказывается информация B, то говорят, что машина применима к последовательности U и перерабатывает ее в последовательность B.

Если остановка и сигнал об остановке никогда не поступают, то говорят, что МТ не применима к последовательности U.

Рассмотрим функционирование МТ на примере сложения двух чисел, которые будем изображать в виде набора единиц.

Внешний алфавит будет состоять из символов: {1, +, Ù}, где Ù – пустой символ.

Внутренний алфавит будет состоять из четырех символов {q₁, q₂, q₃, !}, где символ q₁ означает начальное состояние, а ! – заключительное состояние.

Пусть на ленте записана начальная информация:

						+

МТ должна ее переработать в результирующую информацию:

Абстрактная программа, реализующий операцию сложения, будет иметь вид:

1q1 →Ùq3П 1q3→1q3П +q3→+q3П

Ùq3→1q2H +q2 →+q2Л 1q2→1q2Л Ùq2 →Ùq1П +q1 →Ù!Н

Начальное состояние УУ=q1, состояние ленты имеет вид:

					+

После первого шага состояние YY=q3, состояние ленты как на рис.

					+

					+

После пятого шага YY перейдёт в состояние q2. Состояние ленты показано на рис.

После десятого шага YY в состоянии q1 (рис. )

					+

Последовательность команд, реализующих операцию сложения, удобно задать таблицей, которую называют функциональной схемой алгоритма.

	q1	q2	q3
	Ùq3П	1q2Л	1q3П
Ù	Ùq1П	Ùq1П	1q2H
+	Ù!Н	+q2Л	+q3П

Задания:

1. По заданной машите Тьюринга найти результат ее работы, если

а. A={1,0}, u=1010101,

	q1	q2
	0q2П	0q2Л
	1q0Н	0q1П

б. A={1,0}, u=111

	q1	q2
	1q1П	0q2Л
	0q2Л	1q0Н

в. A={1,0}, u=1001011

	q1	q2
	0q2П	1q2Л
	1q0Н	0q1П

г. A={1,0}, u=110001

	q1	q2	q3
	1q3П	1q2Н	1q1П
	1q2П	1q3П	1q0Н

1. Машина Тьюринга с внешним алфавитом A = {a₀, 1} и алфавитом внешних состояний Q = {q₀, q₁, ... , q₁₃} определяется следующей функциональной схемой:

Q	A
a0	1
q1	q2a0L	q01
q2	q5a0	q3 a0
q3	q4a0L	q01
q4	q51	q41L
q5	q0a0	q61L
q6	q0a0	q7a0
q7	q8a0R	q01
q8	q91	q81R
q9	q0a0	q101L
q10	q0a0	q11a0
q11	q12a0L	q01
q12	q131	q121L
q13	q0a0	q01

Изображая на каждом такте работы машины получающуюся конфигурацию, определите, в какое слово перерабатывает машина следующие слова (в начальный момент времени машина находится в состоянии q₁ и обозревает крайнюю правую ячейку, в которой записан пустой символ a₀ , в следующей слева ячейке уже записан символ a₀1 a₀111 a₀.

Примеры решения Машины Тьюринга:

1. По заданной машите Тьюринга найти результат ее работы, если

A={1,0}, u=111,

	q1	q2
	1q2П	0q2Л
	1q0Н	0q1П

Решение:

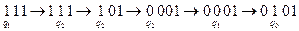
2. Машина Тьюринга с внешним алфавитом A = {a₀, 1} и алфавитом внешних состояний Q = {q₀, q₁, ... , q₁₃} определяется следующей функциональной схемой:

Q	A
a0	1
q1	q2a0L	q01
q2	q5a0	q3 a0
q3	q4a0L	q01
q4	q51	q41L
q5	q0a0	q61L
q6	q0a0	q7a0
q7	q8a0R	q01
q8	q91	q81R
q9	q0a0	q101L
q10	q0a0	q11a0
q11	q12a0L	q01
q12	q131	q121L
q13	q0a0	q01

Изображая на каждом такте работы машины получающуюся конфигурацию, определите, в какое слово перерабатывает машина следующие слова (в начальный момент времени машина находится в состоянии q₁ и обозревает крайнюю правую ячейку, в которой записан пустой символ a₀ , в следующей слева ячейке уже записан символ a₀11 a₀1111 a₀.

Решение:

a₀11 a₀1111 a₀

a₀11 a₀1111 a₀ q₁® a₀11 a₀1111 q₂ a₀ ® a₀11 a₀111 a₀ q₃ a₀ ® a₀11 a₀111 q₄ a₀a₀ ® a₀11 a₀11 q₄ 1a₀a₀ ® a₀11 a₀1 q₄ 11a₀a₀ ® a₀11 a₀ q₄ 111a₀a₀ ®

a₀11 1 q₅ 111a₀a₀ ® a₀11 q₆ 1111a₀a₀ ® a₀1 a₀ q₇ 1111a₀a₀ ® a₀1 a₀ 1 q₈111a₀a₀ ® a₀1 a₀ 11q₈11a₀a₀ ® a₀1 a₀ 111q₈1a₀a₀ ® a₀1 a₀ 1111q₈a₀a₀ ®

a₀1 a₀ 1111a₀q₈a₀ ® a₀1 a₀ 11111q₉a₀ ® a₀1 a₀ 1111q₁₀1a₀ ® a₀1 a₀ 111 a₀q₁₁1a₀ ® a₀1 a₀ 111 q₁₂ a₀1a₀ ® a₀1 a₀ 11 q₁₂ 1a₀1a₀ ® a₀1 a₀ 1 q₁₂ 11a₀1a₀ ®

a₀1 a₀ q₁₂ 111a₀1a₀ ® a₀1 1 q₁₃ 111a₀1a₀ ® a₀1 1 q₀ 111a₀1a₀

Получаем слово: a₀1 1 q₀ 111a₀1a₀

Контрольные вопросы и задания:

1) Из каких частей состоит Машина Тьюринга?

2) Что представляет собой информационная лента?

3) Как работает управляющее устройство?

4) Как выглядит элементарная операция Машины Тьюринга?

Рекомендуемая литература: 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.8, 2.3, 2.4, 2.5.

Практическое занятие №3 " Применение программы Машины Тьюринга "

Цель:Закрепить навыки разработки алгоритмов для составления программы машины Тьюринга и научится применять программу машины Тьюринга.

Вид работы: фронтальный.

Время выполнения: 4 часа.

Теоретический материал:

Программная система моделирования работы машины Тьюринга.

С помощью программного комплекса "Машина Тьюринга" Вы можете изучать на примерах принципы работы столь необычного вычислительного устройства – машины Тьюринга (МТ). Кроме того Вы можете сами создавать, отлаживать и исполнять полноценные программы МТ, а также проверять их формальную корректность и собирать подробную статистику выполнения.
Отличительные черты:

• Возможность быстрого и эффективного редактирования алгоритма, его сохранения в файл или загрузки в любой момент времени.
• Быстрое добавление повторяющихся данных на ленту.
• Возможность проверки условной корректности написанных программ.
• Исполнение и отладка в трех режимах, ведение статистики переходов и применяемых правил.
• Удобный в использовании оконный интерфейс приложения.
• Наличие расширенной справочной системы.
• Возможность приобретения исходных кодов для изучения устройства ПС.

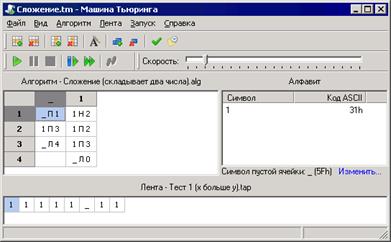
Для добавления строки алгоритма сначала определите место вставки путем выделения ячейки таблицы выше или ниже предполагаемой новой. Затем выберите пункт меню Алгоритм -> Добавить строку, или кликните на кнопку на панели инструментов, или нажмите <Ins>. При этом появится диалоговое окно "Добавить строку":

Для того чтобы удалить строку алгоритма, сначала выберите ее путем выделения одной из ячеек на линии, а затем выберите пункт меню Алгоритм -> Удалить строку, или кликните на кнопку на панели инструментов, или нажмите <Ctrl>+<Del>. В случае, если выбранная строка была единственной описанной в таблице, будет выдано информационной сообщение о невозможности выполнения операции.

При удалении происходит автоматическая корректировка уже заполненных данных таблицы: команды, делавшие переход в удаленное состояние, вычищаются (ячейки делаются пустыми), происходит перенумерация всех состояний после удаленного и исправление ссылок на них (установка новых индексов при их упоминании в уже определенных инструкциях).

Для добавления нового столбца – нового обрабатываемого алгоритмом символа, сначала определите место вставки путем выделения ячейки таблицы слева или справа от предполагаемого нового. Затем выберите пункт меню Алгоритм -> Добавить столбец, или кликните на кнопку на панели инструментов, или нажмите <Shift>+<Ins>. При этом появится диалоговое окно "Добавить столбец":

Для того чтобы удалить столбец, определяющий конкретный обрабатываемый символ алгоритма, сначала выберите его путем выделения одной из ячеек на вертикальной линии, а затем выберите пункт меню Алгоритм -> Удалить столбец, или кликните на кнопку на панели инструментов, или нажмите <Shift>+<Ctrl>+<Del>. В случае, если выбранный столбец определял обрабатываемый символ пустой ячейки, будет выдано информационной сообщение о невозможности выполнения операции.

При удалении столбца происходит автоматическая корректировка уже заполненных данных: при использовании удаленного обрабатываемого символа в качестве аргумента <Новый символ> в какой-либо инструкции таблицы последняя вычищается (делается пустой, неописанной командой).

Символ пустой ячейки играет важную роль в работе алгоритма и определяет символ, которым заполнена условно бесконечная лента машины Тьюринга. Для его изменения выберите пункт меню Алгоритм -> Изменить символ пустой ячейки, или кликните кнопку , или нажмите комбинацию клавиш <Ctrl>+<E>. При этом появится следующее диалоговое окно:

Ввод команд алгоритма производится путем заполнения с клавиатуры соответствующих ячеек таблицы. При этом необходимо соблюдать следующий формат ввода (в нем аргументы должны быть разделены пробелами): <Новый символ> <Перемещение> <Новое состояние>,

где <Новый символ> - один из уже описанных алгоритмом символов;

<Перемещение> - один из символов: Л, П, Н, - означающих переход каретки влево, вправо или указание оставаться на месте;

<Новое состояние> - номер одного из задействованных в алгоритме состояний.

Пример правильного ввода команды: _ Н 0, - означает напечатать символ _, оставаться на месте и перейти в нулевое (завершающее состояние).

Для пущего удобства предусмотрены возможности сохранения набранного алгоритма в файл и загрузки уже подготовленных наборов команд из написанных кем-то программ-проектов. Эти функции доступны в меню Алгоритм с помощью пунктов Загрузить файл и Сохранить файл. Функция Сохранить файл как предназначена для сохранения алгоритма в файл под новым именем.

Под условно бесконечной в обе стороны лентой МТ в данной системе понимается ее значащий участок, доступный для редактирования с помощью режимных окон и непосредственного заполнения с интерфейса главного окна приложения. Важную роль в представлении ленты играет также начальное положение устройства чтения/записи (головки), которое задается путем установки фокуса на отдельной ячейке.

Для того чтобы добавить несколько символов на ленту, для начала определите место вставки путем выбора ячейки слева или справа от предполагаемых новых. Затем выберите пункт меню Лента -> Добавить ячейки, или кликните на кнопку на панели инструментов, или нажмите <Shift>+<Ctrl>+<Ins>. При этом появится диалоговое окно "Добавить ячейки":

Для того чтобы удалить выбранную ячейку ленты, выберите пункт меню Лента -> Удалить ячейку, или кликните на кнопку на панели инструментов, или нажмите <Ctrl>+<D>. В случае, если на ленте оставался один единственный символ, будет выдано информационной сообщение о невозможности выполнения операции.

Для установки начальной позиции головки достаточно выделить конкретную ячейку ленты – при выполнении именно с нее начнет свою работу алгоритм. Будьте внимательны: многие алгоритмы при старте с незапланированных мест могут выдавать неверные результаты, а то и вовсе приходить в неописанные состояния, что приводит к останову процесса выполнения программы.

В системе предусмотрены возможности сохранения исходных данных ленты в файл и загрузки уже подготовленных наборов символов из существующих тестовых примеров. Упомянутые функции доступны в меню Лента с помощью пунктов Загрузить ленту и Сохранить ленту. Функция Сохранить ленту как предназначена для сохранения данных ленты в файл под новым именем.

Под исполнением понимается процесс пошагового выполнения команд алгоритма, что приводит к изменению ленты, а точнее данных на ней. В системе доступно три режима исполнения программ: обычный, быстрый и т.н. пошаговый. Перед запуском в любом режиме сначала производится обязательная проверка программ на синтаксическую и семантическую корректность.

Проверка программы необходима для установления факта корректности алгоритма и соответствия данных на ленте набранному алфавиту. Также по ее завершению делается вывод о возможности исполнения программы.

Процесс проверки состоит из двух этапов. На первом происходит верификация данных на ленте: в случае нахождения символов, отсутствующих в заданном алфавите, в отчет выводится список ошибочных ячеек с указанием их содержимого в скобках. На втором проверяется наличие хотя бы одного перехода в завершающее состояние, в случае его отсутствия – выдача в отчет ошибки. По окончании двух этапов подводится итог: при наличии хотя бы одного замечания пользователь информируется о невозможности запуска программы на исполнение.

Для того чтобы запустить программу в обычном режиме, выберите пункт меню Запуск -> Старт, или кликните на кнопку , или нажмите <F9>. При этом, в случае корректности программы, начнется пошаговый процесс симуляции с отображением состояния машины Тьюринга на интерфейсе приложения: в таблице и на ленте. Скорость выполнения задается с помощью соответствующего ползунка на панели инструментов (по направлению слева направо: от меньшей к большей).

Чтобы приостановить программу, нажмите кнопку , или комбинацию клавиш <Ctrl>+<P>, или выберите пункт меню Запуск -> Пауза. При этом Вы перейдете в пошаговый режим, в котором будет возможность выполнения текущей инструкции по нажатию клавиши <F8> (что эквивалентно нажатию кнопки или выбору пункта меню Запуск -> Сделать шаг). В любой момент времени вы можете снова вернуться в обычный режим, выполнив функцию Старт.

Программа сама остановит свою работу в случае перехода в завершающее состояние. При этом в отчет будет выведена вся статистика работы: порядок и количество примененных правил, результат выполнения и длины входных и выходных данных. Программу, которая не завершает свою работу в течение длительного времени, можно считать зациклившейся, особенно если последнее удается проследить по визуальному отображению хода выполнения. В этих случаях следует вручную остановить процесс исполнения, нажав кнопку , или выбрав пункт меню Запуск -> Остановить, или применив комбинацию клавиш <Ctrl>+<F2>.

Режим доступен по нажатию кнопки на панели инструментов или по альтернативным вариантам: выбору пункта меню Запуск -> Пошаговый режим либо по нажатию комбинации клавиш <Shift>+<Ctrl>+<F9>. При этом эффект от выполнения функции будет эквивалентен запуску в обычном режиме и одновременному постанову на паузу, что полезно при желании отлаживать программу пошагово с самого первого шага.

Режим предназначен для быстрого просчета результата работы заведомо правильных программ, либо для определения факта зацикленности после прохождения большого количества шагов алгоритма.

Для запуска в быстром режиме нажмите кнопку , либо выберите пункт меню Запуск -> Быстрый режим, либо нажмите комбинацию клавиш <Ctrl>+<Q>. При этом, в случае корректности программы, появится диалоговое окно "Выполнить в быстром режиме":

Ход работы и задания:

Составить словесный алгоритм и программу для конструирования Машины Тьюринга для функций. Сделать проверку работы программы не менее чем на трех примерах.

1. F(x)=x+y
2. F(x)=x-y
3. F(x)=2x+y
4. F(x)=3x
5. F(x): остаток от деления на 2
6. F(x)= 2y
7. F(x): остаток от деления на 3
8. F(x)=x+2y

Контрольные вопросы:

1. Опишите состав и схему работы машины Тьюринга.

2. Перечислите этапы конструирования машины Тьюринга.

3. Когда функция вычислима по Тьюрингу?

Рекомендуемая литература: 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.8, 2.3, 2.4, 2.5.

Практическое занятие №4 "Вычисление сложности работы алгоритмов различными методами"

Цель:. Сформировать и закрепить практические навыки оценки временной и емкостной сложности алгоритмов

Вид работы: фронтальный.

Время выполнения: 4 часа.

Теоретические сведения

Основными мерами сложности алгоритма являются время, необходимое для его реализации, и объем требуемой памяти. При этом каждому классу задач можно сопоставить число, характеризующее объем входных данных, которое принято называть размером входа. Например, в задаче логического вывода на основе метода резолюций размером входа следует считать число дизъюнктов исходного множества, в процедуре поиска контрарной пары в двух дизъюнктах - число литералов в этих дизъюнктах и т.д. Очевидно, что сложность алгоритма является функцией размера входа.

Временной сложностью алгоритма называется время, затрачиваемое на вычисление результата, выраженное как функция размера входа. Емкостная сложность - общая емкость памяти, использованной в процессе реализации алгоритма, как функция размера входа.

Сложность алгоритма может быть различной и при фиксированном размере входа, но различных входных данных. Например, при поиске контрарной пары в двух дизъюнктах фиксированной длины, контрарные литералы могут оказаться первыми или последними в этих дизъюнктах. Очевидно, что время поиска контрарной пары в этих случаях окажется различным. Поэтому различают сложность в худшем и в среднем случае. Сложность в худшем случае - это максимальная при данном размере входа сложность. Средняя сложность - средняя по всем входам данного размера сложность.

Временная сложность в худшем случае - это функция T(n), равная максимальной (по всем входам размера n) из сумм времен, затраченных на каждую сработавшую команду (оператор).

Емкостная сложность в худшем случае - это функция S(n), равная максимальной (по всем входам размера n) из сумм емкостей всех ячеек (элементов) памяти к которым было обращение.

Для точного теоретического определения временной и емкостной сложности требуется знать времена выполнения каждой команды (оператора) и объем памяти, используемый каждой переменной. Так как эти значения зависят от конкретной вычислительной машины, в теории сложности алгоритмов принято оценивать порядок сложности.

Говорят, что функция f(n) имеет сложность порядка g(n), если существуют такие положительные константы c и n₀, что для всех n ³ n₀ , f(n) £ c * g(n) [7]. Этот факт записывается так: f(n) есть O(g(n)). Обычно рассматриваются положительные функции натуральных чисел. Например, функция f(n) = 10*n³ есть O(n³), т.к. существуют c=10 и n₀ = 1, для которых 10*n³ £ 10*n³ . Неверно, что 10*n³ есть O(n²), так как для любого сколь угодно большого наперед заданного значения константы c найдется такое значение n₀ аргумента, что f(n) ³ c * g(n) для всех n ³ n₀.

При оценке порядка временной сложности определяется зависимость числа шагов в алгоритме от размера входа. Шагом считается такой фрагмент алгоритма, время реализации которого не зависит от размера входа, а число реализаций этого фрагмента зависит от размера входа. Например, шагом является тело цикла, независимо от числа содержащихся в нем операторов, если оно не содержит вложенных циклов, а параметр цикла связан с размером входа.

При определении порядка емкостной сложности, в качестве единицы необходимо выбрать некоторый элементарный в данном классе алгоритмов объект. Таким объектом в задаче логического вывода на основе метода резолюций следует считать литерал. При этом точный объем памяти (в байтах), занимаемой одним литералом, зависит от выбранных типов и структур данных и не влияет на порядок сложности.

При теоретическом анализе порядка сложности алгоритмов принято оценивать сложность в худшем случае. Теоретическая оценка средней сложности, как правило, весьма затруднительна, т.к. предполагает учет всевозможных комбинаций входных данных и вероятностей их появления. Она может быть получена (в некотором приближении) экспериментальным путем с помощью программно реализованного алгоритма.

При оценке сложностей могут использоваться различные критерии.

Равномерный весовой критерий предполагает, что каждая команда (оператор) затрачивает одну единицу времени и каждая переменная в алгоритме занимает одну ячейку памяти, независимо от принимаемых ей значений.

Логарифмический весовой критерий учитывает ограниченность размера реальной ячейки памяти. Пусть l(i)- логарифмическая функция на целых числах, определенная следующим образом:

æ [ log₂¦ i ¦ ] + 1, при i ¹ 0;

l(i) = í

è 1 , при i=0.

Здесь [...] - округление до меньшего целого.

Логарифмический критерий при оценке временной сложности основан на допущении, что время выполнения команды зависит от величины обрабатываемых операндов и определяется значением l(i), где i - величина обрабатываемого данной командой операнда.

Логарифмический критерий при оценке емкостной сложности учитывает размер ячейки (в битах) в зависимости от величины операнда. Логарифмическая емкостная сложность - сумма по всем использованным ячейкам величин l(x_i), где x_i - наибольшее по абсолютной величине значение, содержавшееся в i-ой ячейке за все время вычислений.

Алгоритм может иметь существенно различные временные и емкостные сложности в зависимости от используемого весового критерия.

Пример. Определить временную и емкостную сложность алгоритма сортировки массива по возрастанию методом «пузырька» при равномерном и логарифмическом весовых критериях.

Решение. В соответствии с данным методом для всех элементов массива, начиная со второго, последовательно выполняется «всплывание», при котором текущий элемент, если он меньше предыдущего, меняется с ним местами. Обозначим i - текущий номер элемента при просмотре массива в глубину, j - номер текущего элемента при "всплывании" (процедура elem_up), A(j) - j-ый элемент массива, n - число элементов в массиве. Тогда, используя синтаксис языка Паскаль, можно записать:

program Sort;

procedure elem_up (i: integer); {процедура «всплывание» элемента}

begin

j := i

while (j > 1) and (A(j) < A(j-1)) do

begin

X:= A(j); {перестановка соседних элементов}

A(j):=A(j-1);

A(j-1):=X;

j := j-1;

end

end;

begin {основной цикл программы}

for i := 2 to n do elem_up(i);

end.

Временная сложность при равномерном весовом критерии. Очевидно, что размером входа для данного алгоритма следует считать число n элементов в массиве, а шагом алгоритма - тело цикла в процедуре «всплывание». В теле основной программы имеем (n-1) проходов по циклу. В процедуре elem_up ("всплывание" элемента) - в худшем случае выполняется i проходов по циклу. Тогда, общее число шагов в алгоритме равно:

n

å i = (n+2)*(n-1)/2 = (n²+n-2)/2 .

i=2

Таким образом, временная сложность алгоритма при равномерном весовом критерии есть O(n²).

Временная сложность при логарифмическом весовом критерии. Логарифмическая временная сложность операций инкрементации и сравнения с граничным значением параметра цикла в основной программе на i-ом проходе есть log(i). Суммарная сложность этих операций на всех проходах основной программы:

n

å log(i) = log(n!)

i=2

В процедуре elem_up логарифмическая временная сложность складывается из двух частей. Во-первых, работа со счетчиком "всплывания" j. Так как он выполняет обратный счет от i до 1, то временная сложность этой операции для i-го прохода цикла основной программы есть:

log(i) + log(i-1) + ... + log1 = log(i!).

За время всех n проходов:

n n

ålog(i!) = log(Õ(i!)) .

i=2 i=2

Во-вторых, работа с элементами массива (их сравнение и перестановка). Логарифмическая сложность этой операции определяется значениями элементов массива и равна log(A_max), где A_max - максимальное значение элементов массива. Число шагов на i-ом проходе основной программы в худшем случае равно i*log(A_max). За все проходы имеем:

n

å(i*log(A_max)) = (n*(n+1)/2)*log(A_max).

i=2

Тогда суммарная временная сложность при логарифмическом критерии есть: n

log(n!) + log(Õ(i!)) + (n*(n+1)/2)*log(A_max).

i=1

Окончательно для временной сложности при логарифмическом весовом критерии имеем

n

O(MAX(log(Õ(i!)), n²*log(A_max)).

i=1

Емкостная сложность при равномерном весовом критерии. Очевидно определяется размером n массива, поэтому есть O(n).

Емкостная сложность при логарифмическом весовом критерии. Определяется с одной стороны размером массива и его элементов, а с другой - емкостью счетчика:

log(n) + n*log ¦A_max¦.

Окончательно имеем O(n*log ¦A_max¦).

Задание:

Определить временную и емкостную сложность алгоритмов решения следующих задач при равномерном и логарифмическом весовых критериях.

- Вычислить n!.

- Вычислить nⁿ.

- Вычислить число размещений A(n,m)= n!/(m!*(n-m)!).

- Упорядочить массив из n целых чисел таким образом, чтобы элементы с четными и нечетными значениями чередовались (пока имеются элементы разной четности).

Контрольные вопросы:

1. Что является временной сложностью?
2. Как определяется оценка порядка временной сложности?
3. Какие критерии используются при оценке сложности?
4. В чем суть логарифмического критерия?

Рекомендуемая литература: 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.8, 2.3, 2.4, 2.5.

СПИСОК ЛИТЕРАТУРЫ

1. Основная литература

1.1 Turbo Pascal. Практикум. 2-е изд. / С.А. Немнюгин. – СПб.: Питер, 2003 – 230 с.

1.2 Turbo Pascal. Программирование на языке высокого уровня: учебное пособие. 2-е изд. / С.А. Немнюгин. – СПб.: Питер, 2004. – 496 с.

1.3 Голицына О.Л. Основы алгоритмизации и программирования. – М: Форум, Инфра-М, 2008. – 432 с.

1.4 Демидович Е.М. Основы алгоритмизации и программирования. – СПб: БХВ-Петербург, 2008. – 440 с.

1.5 Колдаев В.Д. Основы алгоритмизации и программирования: учебное пособие для СПО. – М: Форум, Инфра-М, 2006. – 416 с.

1.6 Культин Н., Turbo Pascal в задачах и примерах: учебное пособие. – СПб: БХВ-Петербург, 2006. – 256 с.

1.7 Лаптев В.В. С++ Объектно-ориентированное программирование: задачи и упражнения: учебное пособие для вузов. – СПб: Питер, 2007. – 288 с.

1.8 Попов В.Б., Turbo Pascal для школьников: учебное пособие. – М: Финансы и статистика, 2003. – 528 с.

1. Дополнительная литература

2.1 Павловская Т.А., Щупак Ю.А. С++. Объектно-ориентированное программирование: Практикум. – СПб.: Питер, 2008. – 264 с.

2.2 Ишкова Э.А. Начала программирования. Изд. 2-е, перерабю и доп. – М.: ЗАО «Изд. БИНОМ», 2006. – 288 с.

2.3 Паскаль. Программирование на языке высокого уровня: Учебник для вузов/ Т.А. Павловская. – СПб.: Питер, 2007 – 325 с.

2.4 Марченко А.И., Марченко Л.А. Программирование в среде Turbo Pascal 7.0/Под ред. Тарасенко В.П. – 6-е изд. – К.:ВЕК+, 2006. – 464 с.

2.5 Пестриков В.М., Маслобоев А.Н. Turbo Pascal 7.0. Изучаем на примерах. – СПб.: Наука и Техника, 2006 – 168 с.

Методические указания

для лабораторных занятий студентов

специальности 230115 Программирование в компьютерных системах