Редактор формул microsoft equation 3.0

Цель работы – приобретение навыков вставки объектов, работы с редактором формул, задания разной ориентации страниц одного документа, ознакомление со структурой текстов, содержащих формулы.

Microsoft Word воспринимает математическую формулу как отдельный объект, связываемый с текстом.

Для вставки математических формул в тексты используется редактор формул Microsoft Equation 3.0, находящийся закладке «Вставка» меню программы:

Вставка®Объект®Microsoft Equation 3.0®…

Рис. 29. Окно вставки объекта Microsoft Equation 3.0

Обратите внимание, чтобы в окне выбора типа вставляемого объекта был отключен флажок «поверх текста»!

После загрузки редактора формул появляется окно для ввода формул, панель инструментов, которую можно перемешать по экрану мышью, и меню редактора (на месте меню текстового процессора).

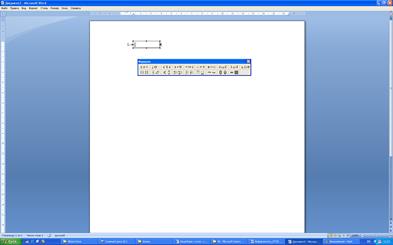
Рис. 30. Рабочее окно редактора формул Microsoft Equation 3.0.

Набор формул производится с клавиатуры (символы английского и русского алфавитов) и с помощью панели инструментов (символы греческого алфавита и математические знаки).

Для выхода из редактора формул достаточно щелкнуть по документу за границами поля ввода формул. Войти в уже имеющуюся формулу для её редактирования можно, наведя курсор мыши на формулу и дважды щелкнув мышью.

Второй способ вставки формулы в текст – обращение к команде «Формула»раздела «Символы» закладки Вставка меню программы. Команда содержит также некоторые готовые объекты. Это способ становится доступен после первого обращения к редактору формул Microsoft Equation 3.0.

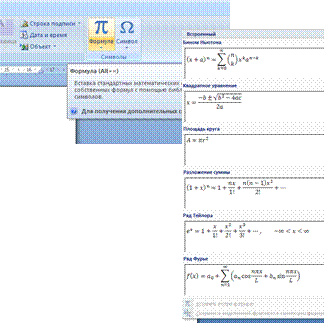
Рис. 31. Окно «Формула» закладки «Вставка».

Начать работу с уже существующей в документе формулой можно выделив формулу (щелчок левой кнопкой мыши по формуле) и обратясь к появившемуся меню «Работа с формулами».

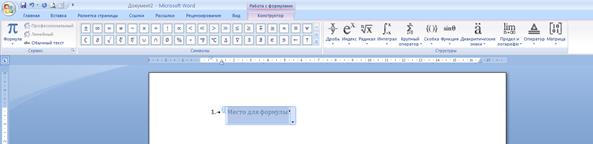
Рис. 32. Панель инструментов меню «Работа с формулами».

Задание 1.

1. Создать новый документ. На первой странице оформить титульный лист.

2. Набрать формулы (табл. ниже), используя редактор формул Microsoft Equation 3.0. Параметры страницы для набора формул: ориентация – альбомная, размеры верхнего и нижнего полей – 2 см, правого – 17 см, левого – 1,7 см. Номер варианта задания соответствует номеру компьютера в компьютерном классе.

Вариант	Задания

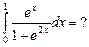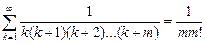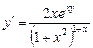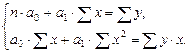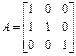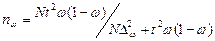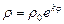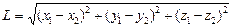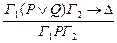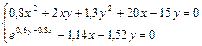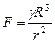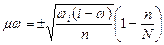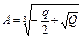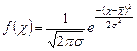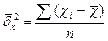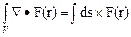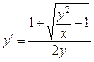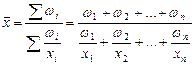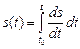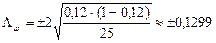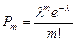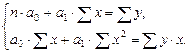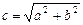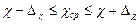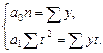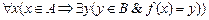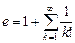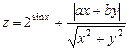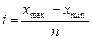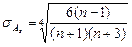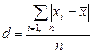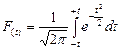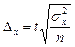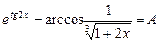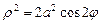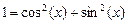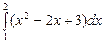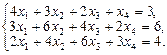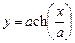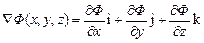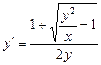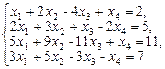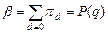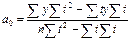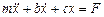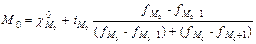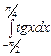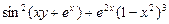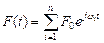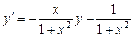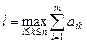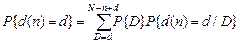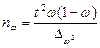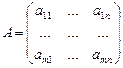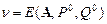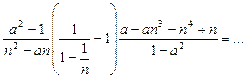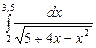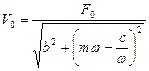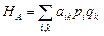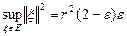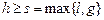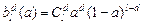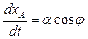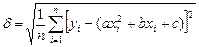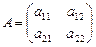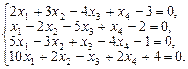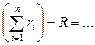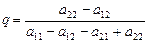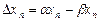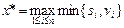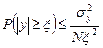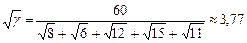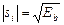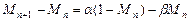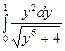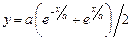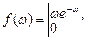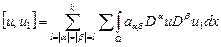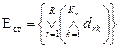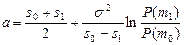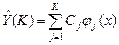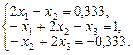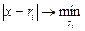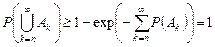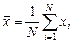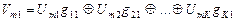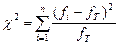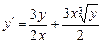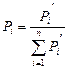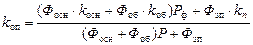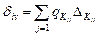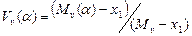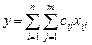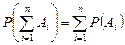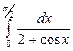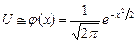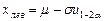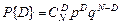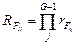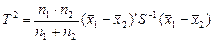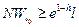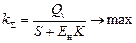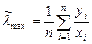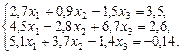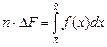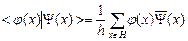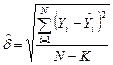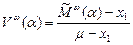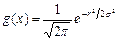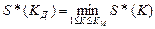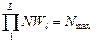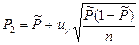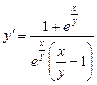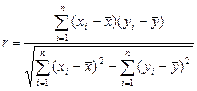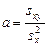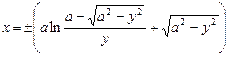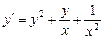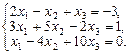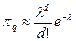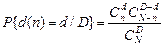Задание 2.

1. На новой странице документа последовательно с интервалом 1,5 см набрать Текст 1 и Текст 2, содержащие формулы. Выдержать заданное оформление текстов. Параметры страницы: ориентация книжная, поля: верхнее и нижнее – 1,5 см, правое и левое – 2 см. Междустрочный полуторный. Шрифт Book Antiqua. Размер шрифта – 13. Отступ первой строки – 1 см.

2. Заархивировать файл в обычный архив и самораспаковывающийся архив.

Текст 1:

Спектральный коэффициент поглощения отдельного компонента в смеси с общим давлением »10⁵ Па может быть вычислен по формуле, описывающей дисперсионный (лоренцовский) контур спектральной линии:

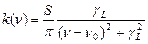, (1)

где g_L – ударная полуширина линии;

S – интегральная интенсивность линии;

n₀ – частота центра линии.

Текст 2:

Основная идея шагового метода состоит в нахождении регрессии с несколькими переменными в виде серий линейных регрессионных зависимостей и в преобразовании исходной корреляционной матрицы шаг за шагом. На каждом шаге получают результаты для анализа дисперсий с помощью F-критерия для проверки двух типов гипотез: одна – для включения переменной в уравнение регрессии; другая – для исключения из него.

Вычислительная процедура состоит в том, чтобы применить линейное преобразование к матрице

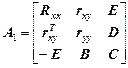, (2)

где R_xx – корреляционная матрица размера m´m; 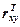– вектор-строка коэффициентов корреляции зависимой и m независимых переменных; r_xy – вектор-столбец коэффициентов корреляции зависимой и m независимых переменных; Е – единичная матрица размера m´m; -Е – отрицательная единичная матрица размера m´m; r_yy – коэффициент корреляции (r_yy= 1); D –вектор-строка с m нулевыми элементами; В – вектор-столбец с m нулевыми элементами; С – матрица размера m´m с нулевыми элементами.