Алгоритм k-средних
По крайней мере в принципе, алгоритм k-средних довольно прост. Но, как вы еще увидите, некоторые детали реализации весьма изощренные. Главной концепцией алгоритма k-средних является центроид (centroid), или центр масс. В кластеризации данных центр масс набора последовательностей данных — это одна из последовательностей, которая является наиболее репрезентативной в группе. Эту идею лучше пояснить на примере. Допустим, у вас есть три последовательности «рост, вес», аналогичные показанным на рис. 1:
[a] (61.0, 100.0)
[b] (64.0, 150.0)
[c] (70.0, 140.0)
Какая последовательность самая репрезентативная? Один из подходов — вычисление средней последовательности с выбором в качестве центра масс той последовательности, которая ближе всего к средней. В данном случае средняя последовательность:
[m] = ((61.0 + 64.0 + 70.0) / 3, (100.0 + 150.0 + 140.0) / 3)
= (195.0 / 3, 390.0 / 3)
= (65.0, 130.0)
А теперь, какая из трех последовательностей ближе всего к (65.0, 130.0)? Есть несколько способов определить ближайшую последовательность. Самый распространенный способ, применяемый в демонстрационной программе, — использование евклидового расстояния, или метрики (Euclidean distance). Если на словах, то евклидово расстояние между двумя последовательностями является корнем квадратным суммы квадратов разностей между соответствующими компонентами каждой последовательности. И вновь это лучше пояснить на примере. Евклидово расстояние между последовательностью (61.0, 100.0) и средней последовательностью (65.0, 130.0) равно:
dist(m,a) = sqrt((65.0 - 61.0)^2 + (130.0 - 100.0)^2)
= sqrt(4.0^2 + 30.0^2)
= sqrt(16.0 + 900.0)
= sqrt(916.0)
= 30.27
Аналогично:
dist(m,b) = sqrt((65.0 - 64.0)^2 + (130.0 - 150.0)^2)
= 20.02
dist(m,c) = sqrt((65.0 - 70.0)^2 + (130.0 - 140.0)^2)
= 11.18
Поскольку наименьшая из трех метрик является расстоянием между средней и последовательностью [c], то центр масс трех последовательностей — [c]. Возможно, вы пожелаете поэкспериментировать с демонстрационной программой, используя разные определения расстояния между двумя последовательностями, чтобы понять, как это влияет на конечную кластеризацию.
Освоив понятие центра масс кластера, вы довольно легко поймете алгоритм k-средних. В псевдокоде:
Назначаем каждую последовательность случайно выбранному кластеру
Вычисляем центр масс каждого кластера
loop пока нет улучшений или не будет достигнут maxCount
Присваиваем каждую последовательность лучшему кластеру
(кластеру с ближайшим центром масс к последовательности)
Обновляем центр масс каждого кластера
(на основе новых назначений кластерам)
end loop
return кластеризованные данные
Поищите в Интернете — найдете несколько хороших онлайновых анимаций, демонстрирующих алгоритм k-средних в действии. Изображение на рис. 2 показывает, к какой кластеризации приводит демонстрационная программа. Элемент данных, обведенный в кружок в каждом кластере, является центром масс этого кластера.
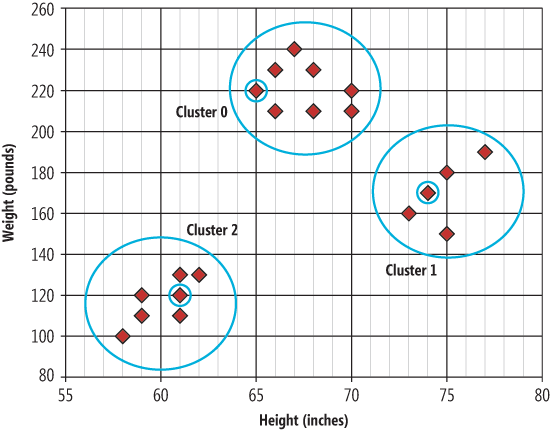
Рис. 2. Кластерные данные и центры масс
| Weight (pounds) | Вес (в фунтах) |
| Cluster 0 | Кластер 0 |
| Cluster 1 | Кластер 1 |
| Cluster 2 | Кластер 2 |
| Height (inches) | Рост (в дюймах) |
