Методы перебора в задачах поиска
Задачи поиска предназначены для определения нахождения элемента, обладающего заданным свойством, в определенной совокупности данных, в частности, в массиве.
Линейный поиск.
Поиск наибольшего и наименьшего элемента в массиве.
Дан ряд чисел 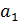 ,
, 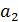 , …,
, …, 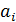 , …,
, …, 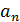 . Разработать алгоритм поиска наибольшего и наименьшего числа в этом ряду с указанием номера (индекса) его расположения.
. Разработать алгоритм поиска наибольшего и наименьшего числа в этом ряду с указанием номера (индекса) его расположения.
Очевидный способ поиска наибольшего (наименьшего) числа в заданном ряду n чисел включает следующие действия. Взять первое число ряда и сказать, что оно наибольшее (наименьшее), а индекс его равен 1. Затем взять второе число ряда и сравнить с предполагаемым максимальным (минимальным) первым числом. Если второе число больше предполагаемого (максимального) первого числа, взять третье число ряда и сравнить с первым. Так следует действовать до тех пор, пока не будет выбрано последнее 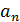 число. В результате на месте первого числа окажется наибольшее (наименьшее) число с указанным его номером в ряду чисел. [2]
число. В результате на месте первого числа окажется наибольшее (наименьшее) число с указанным его номером в ряду чисел. [2]
Блок – схема алгоритма поиска наибольшего и наименьшего элемента на рис.18.

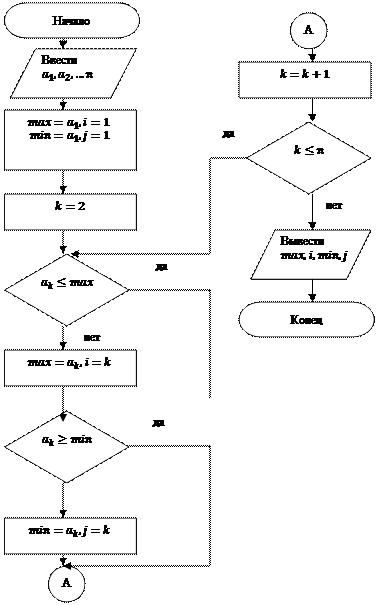
Рис. 18 Алгоритм нахождения наибольшего и наименьшего элемента в линейном массиве
Программа на языке Pascal представлена в Приложении 1, MaxMin.pas.
Бинарный поиск.
Метод бинарного поиска можно применять уже в отсортированном массиве. Допустим, что массив А отсортирован в порядке не убывания. Это позволяет по результату сравнения со средним элементом массива исключить из рассмотрения одну из половин. С оставшейся частью процедура повторяется. И так до тех пор, пока не будет найден искомый элемент или не будет построен весь массив. [6,7]
Рассмотрим алгоритм бинарного поиска на примере.
Пример. Пусть X = 6, а массив А состоит из 10 элементов:
3 5 6 8 12 15 17 18 20 25.
1-й шаг. Найдем номер среднего элемента среднего элементов: m = 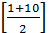 = 5.
= 5.
Так как 6 < А[5], то далее рассматриваются только элементы, индексы которых меньше 5.
3 5 6 8 12 15 17 18 20 25.
2-й шаг. Рассматриваем лишь первые 4 элемента массива, находим индекс среднего элемента этой части : m = 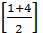 = 2.
= 2.
6 > А[2], следовательно, первый и второй элементы из рассмотрения исключаются:
3 56 8 12 15 17 18 20 25;
3-й шаг. Рассматриваем два элемента, значение m = 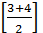 = 3.
= 3.
3 56 8 12 15 17 18 20 25;
А[3] = 6. Элемент найден, его номер – 3.
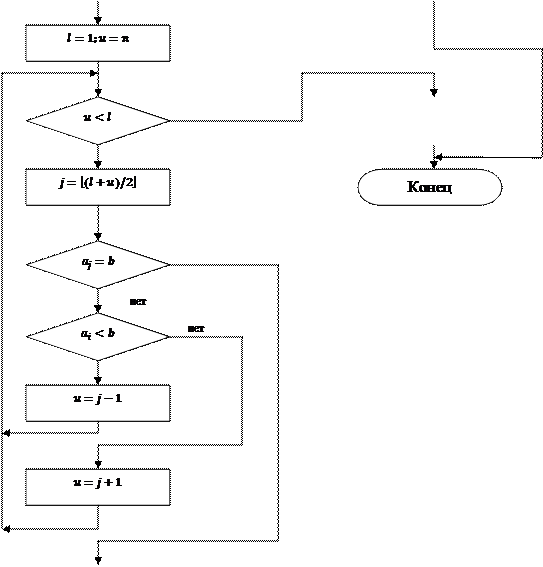
Блок - схема алгоритма бинарного поиска на рис.19:
 | ||||||||||||||
 |  | |||||||||||||
 | ||||||||||||||
 | ||||||||||||||
 | ||||||||||||||
 | ||||||||||||||
|
 | |||||
 | |||||
 |
Программная реализация бинарного поиска представлена в Приложении 1, Binar.pas.
Случайный поиск.
Организация поиска k-го элемента в неупорядоченном массиве X возможна следующим образом. Выбирается случайным образом элемент с номером q. Массив X разбивается на три части: элементы, меньшие X[q], равные X[q]и большие X[q]. А затем, в зависимости от количества элементов в каждой части, выбирается одна из частей для дальнейшего поиска. Теоретическая оценка числа сравнений имеет порядок k*N, т. е. для худшего случая N2, но на практике он значительно быстрее.
СЛОЖНОСТЬ АЛГОРИТМОВ
Характеристики алгоритма, которые влияют на его применимость, принято называть характеристиками сложности алгоритма. Среди характеристик сложности наиболее важными являются две, характеризующие ресурсы исполнителя: время и память. Необходимо знать, как долго будет выполняться алгоритм и хватит ли ресурса памяти для этого. Время зависит от того, кто является исполнителем (человек, вычислительное устройство, компьютер), и от того, насколько быстро он делает операции (разные компьютеры обладают разной производительностью). Так как нужна объективная характеристика алгоритма, не зависящая от исполнителя, то вместо времени исполнения алгоритма будем рассматривать число шагов t выполнения алгоритма. Если 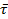 – среднее время одного шага исполнителя, то фактическое время работы алгоритма для этого исполнителя.
– среднее время одного шага исполнителя, то фактическое время работы алгоритма для этого исполнителя.
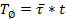
Таким образом, t есть характеристика алгоритма, не зависящая от особенностей исполнителя, и потому математическая характеристика сложности алгоритма. Память S, используемая алгоритмом, также зависит от особенностей исполнителя. Если на каждом шаге алгоритма используется не более µ единиц памяти, то S ≤ µ · 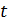 . Эта оценка очень грубая, так как t может значительно превосходить S. В большинстве случаев в качестве характеристики сложности алгоритма применяется характеристика t – число шагов выполнения алгоритма.
. Эта оценка очень грубая, так как t может значительно превосходить S. В большинстве случаев в качестве характеристики сложности алгоритма применяется характеристика t – число шагов выполнения алгоритма.
Трудоемкость алгоритмов.
Итак, 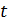 зависит от исходных данных задачи. Зависимость эту не всегда возможно анализировать непосредственно. Вследствие этого целесообразно будет определить временные рамки выполнения алгоритма (максимальное и минимальное время), сколько в среднем будет выполняться алгоритм (среднее время). Но для любых вариантов задачи время (число шагов) ничем не ограничено. Так, при сортировке массива время, как правило, зависит от длины массива и растет с ростом числа элементов массива. Принято входные данные
зависит от исходных данных задачи. Зависимость эту не всегда возможно анализировать непосредственно. Вследствие этого целесообразно будет определить временные рамки выполнения алгоритма (максимальное и минимальное время), сколько в среднем будет выполняться алгоритм (среднее время). Но для любых вариантов задачи время (число шагов) ничем не ограничено. Так, при сортировке массива время, как правило, зависит от длины массива и растет с ростом числа элементов массива. Принято входные данные 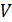 алгоритма характеризовать одним параметром или несколькими параметрами. Одной из таких характеристик является объем входных данных – число элементов входных данных. Эта характеристика объективно характеризует входные данные так же, как и число шагов объективно характеризует исполнение алгоритма. В свою очередь, устанавливают зависимость объема входных данных от одного или нескольких параметров, характеризующих задачу. Так, в задаче сортировки массива таким параметром является длина n массива.
алгоритма характеризовать одним параметром или несколькими параметрами. Одной из таких характеристик является объем входных данных – число элементов входных данных. Эта характеристика объективно характеризует входные данные так же, как и число шагов объективно характеризует исполнение алгоритма. В свою очередь, устанавливают зависимость объема входных данных от одного или нескольких параметров, характеризующих задачу. Так, в задаче сортировки массива таким параметром является длина n массива.
Так как число шагов алгоритма зависит не только от выбранных в задаче параметров 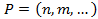 , характеризующих объем входных данных
, характеризующих объем входных данных  но и от других характеристик входных данных
но и от других характеристик входных данных
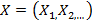 , то можно ввести оценку по всем этим характеристикам. Оценка наибольшего числа шагов, необходимых для выполнения алгоритма, в зависимости от параметров P:
, то можно ввести оценку по всем этим характеристикам. Оценка наибольшего числа шагов, необходимых для выполнения алгоритма, в зависимости от параметров P:
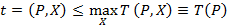
называется максимальной трудоемкостью алгоритма или просто трудоемкостью алгоритма. Максимальная трудоемкость дает возможность оценить максимальное время, необходимое для исполнения алгоритма. Эта оценка может быть очень завышенной в некоторых случаях. Поэтому важно иметь оценку наименьшего числа шагов, которую называют минимальной трудоемкостью:
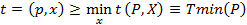
и оценку среднего числа шагов, которую называют средней трудоемкостью:
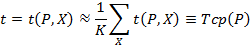
где k – число вариантов других характеристик входных данных.
Трудоемкость алгоритма позволяет оценить время выполнения алгоритма при решении той или иной задачи:
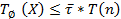
При этом коэффициент 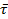 статистически определяется для исполнителя или оценивается некоторой константой. Однако точный вид зависимости T(n) от аргумента n часто очень трудно установить. Поэтому вместо установления вида функции для трудоемкости оценивается быстрота роста этой функции при помощи некоторой простой функции f(n).
статистически определяется для исполнителя или оценивается некоторой константой. Однако точный вид зависимости T(n) от аргумента n часто очень трудно установить. Поэтому вместо установления вида функции для трудоемкости оценивается быстрота роста этой функции при помощи некоторой простой функции f(n).
Говорят, что T(n) = O(f(n)), если |T(n)| ≤ C|f(n)| для всех значений n > n0. Такая оценка роста функции T(n) является односторонней, так как функция f(n) может расти быстрее. Лучше оценивать рост трудоемкости функцией f(n), имеющей тот же порядок роста, т. е. также |T(n)| ≥ C1|f(n)|. В этом случае пишут
T(n) = Θ(f(n)) и говорят, что рост T(n) оценивается ростом f(n). Наиболее простыми функциями, оценивающими рост трудоемкости, являются полиномы
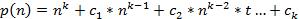
В случае T(n) = Θ(p(n)), учитывая, что p(n) = Θ(n k ), получаем T(n) = Θ(n k). Говорят, что в этом случае трудоемкость полиномиальна или алгоритм имеет полиномиальную трудоемкость. При k = 1 T(n) = Θ(n) и алгоритмы принято называть алгоритмами с линейной трудоемкостью.
Если есть два алгоритма A1 и A2 решения некоторой задачи и оба имеют полиномиальную трудоемкость, причем k1 < k2, то говорят, что первый алгоритм имеет меньшую трудоемкость. Но меньшая трудоемкость не означает, что время решения задачи первым алгоритмом будет меньше, чем вторым. Так, пусть
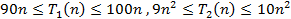
Тогда при n < 10 оказывается, что время решения задачи для первого алгоритма больше, чем для второго. Однако, из определения ясно, что найдется такое n0 (в примере n0 = 10), что время решения задачи при n > n0 будет всегда меньше для первого алгоритма.
Трудоемкость алгоритма может иметь скорость роста меньшую, чем линейная. Например, 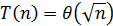 или
или 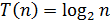 .
.
Но и в этом случае принято говорить о полиномиальной трудоемкости. Алгоритмы, трудоемкость которых растет быстрее любого полинома, принято называть алгоритмами экспоненциальной трудоемкости, даже если скорость роста трудоемкости оценивается более медленной функцией, чем экспонента. Например, экспоненциальными являются все алгоритмы со следующими трудоемкостями:
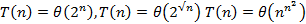
Причина, по которой используются только эти два названия трудоемкости (полиномиальная и экспоненциальная), состоит в том, что алгоритмы полиномиальной трудоемкости, как правило, эффективны, если показатель степени у полинома не слишком большой. А алгоритмы экспоненциальной трудоемкости не являются эффективными, так как время вычисления по этим алгоритмам растет очень быстро. В таблице показана скорость нарастания времени работы алгоритмов различной трудоемкости в секундах на компьютере с быстродействием 106 оп/сек.
| n | |||||
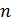 | 0.00001 | 0.00002 | 0.00003 | 0.00004 | 0.00005 |
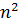 | 0.0001 | 0.0004 | 0.0009 | 0.00016 | 0.00025 |
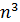 | 0.001 | 0.008 | 0.0027 | 0.0064 | 0.125 |
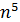 | 0.1 | 3.2 | 24.3 | 1.7 мин | 5.3 мин |
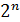 | 0.001 | 1.0 | 17.9 мин | 12,7 дн | 35,7 лет |
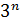 | 0.059 | 58 мин | 6.5 лет | 385500 лет | 200 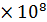 лет лет |
При нескольких параметрах входных данных трудоемкость полиномиального алгоритма растет как полином от нескольких аргументов. Например,
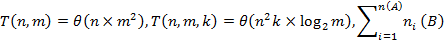
Оценивание трудоемкости алгоритмов.
Процесс получения оценки трудоемкости называется оцениванием трудоемкости. Для этого следует анализировать алгоритм с точки зрения быстроты роста числа его шагов, при изменении параметров задачи (параметров входных данных). Прежде всего, в алгоритме следует выделить циклы. Если циклов нет, то число шагов линейной структуры алгоритма не зависит от параметров задачи и, следовательно, трудоемкость является константной, т. е. оценивается как Θ (1).
Циклическая структура алгоритма ведет к повторению выполнения его частей, что влияет на общее число шагов выполнения, т. е. на трудоемкость. Следует оценить для каждого цикла, от каких параметров задачи зависит число повторений цикла и как оно растет с ростом этих параметров.
Если цикл B с числом повторений n(B) вложен в цикл A с числом повторений n(A) и циклы независимы (число повторений цикла B не зависит от выполнения цикла A), то общее число повторений цикла B с учетом повторений цикла A составляет n(A) · n(B).
Отсюда правило: для вложенных независимых циклов их трудоемкости перемножаются Θ(AB) = Θ(A) · Θ(B).
Если вложенные циклы не являются независимыми, т. е. число повторений внутреннего цикла ni(B) зависит от номера i повторения при выполнении внешнего цикла, то нужно проанализировать, как зависит общее число повторений внутреннего цикла от параметров задачи.
Если циклы не являются вложенными, то трудоемкость определяется наибольшей из трудоемкостей циклов
Θ(A + B) = Θ(A) + Θ(B) = max{Θ(A), Θ(B)}.
При оценке максимальной трудоемкости следует подбирать такие примеры входных данных для тех или иных параметров задачи, на которых реализуется максимальное число шагов алгоритма. При оценке минимальной трудоемкости следует подбирать примеры, на которых реализуется минимальное число шагов алгоритма. Ввиду сложности некоторых алгоритмов такие примеры не всегда удается построить, но в таких случаях для оценки трудоемкости бывает достаточно примеров и близких по числу операций к максимальному или соответственно к минимальному числу.[11]
Рассмотрим примеры оценивания трудоемкости на примере алгоритма сортировки массива методом «пузырька». Блок – схема алгоритма сортировки методом «пузырька» см. рис. 15
Алгоритм содержит вложенные циклы. Внешний цикл, в случае массива входных данных, упорядоченного по убыванию, будет выполняться максимальное число раз: n − 1, а в случае входного массива, упорядоченного по возрастанию, будет выполняться только 1 раз. Внутренний цикл во втором случае выполняется n − 1 раз, а в первом случае циклы зависимы, но, внутренний цикл в среднем выполняется n/2 раз. Поэтому максимальная трудоемкость (входные данные первого случая) оценивается как
Θ(n) · Θ(n) = Θ(n2),
а минимальная трудоемкость (входные данные второго случая) – как
Θ(1) · Θ(n) = Θ(n).
Во втором разделе рассмотрены методы сортировки элементов массива: метод простого выбора, метод «пузырька», сортировка слиянием и вставками. Разобран типовой пример нахождения максимального и минимального элементов в массив и принцип бинарного поиска в упорядоченном массиве. Для закрепления навыков создания алгоритмов сортировки можно рекомендовать задания для самостоятельной работы.
