Метод узловых потенциалов
Применение данного расчетного метода позволяет уменьшить количество уравнений системы до (n – 1), где n – число узлов электрической цепи. Порядок расчета данным методом следующий:
1. Потенциал одного из узлов (любого) условно принять равным нулю. Этот узел называют опорным.
2. Для расчета неизвестных (n – 1) потенциалов составить систему уравнений, записываемую в виде матричного уравнения вида
,
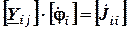где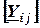 
– квадратная матрица комплексных проводимостей, в которой:
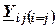– собственная комплексная проводимость, определяемая как сумма проводимостей ветвей, сходящихся в узле;
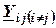– общая комплексная проводимость ветвей, соединяющих i и j узлы, определяемая как проводимость ветви, соединяющей i и j узлы. В случае, если между i и j узлами подключены несколько ветвей (не имеющих промежуточных узлов), общая проводимость определяется как сумма проводимостей ветвей, соединяющих узлы. Общая проводимость в системе уравнений всегда берется со знаком минус.
В н и м а н и е! Проводимость ветви, содержащей источник тока, равна 0.
Д о п о л н е н и е. Для цепей, в ветвях которых подключены только идеальные источники напряжения (Rветви = 0), расчет может быть упрощен при выборе опорного узла на выводах этих ветвей. Тогда потенциал одного из узлов становится известным и равным ЭДС идеального источника напряжения. Таким образом, количество совместно рассматриваемых уравнений системы сокращается. Однако следует отметить, что оставшиеся уравнения остаются неизменными, т.е. содержат слагаемые, являющиеся произведением известного потенциала узла и соответствующей проводимости.
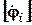– матрица-столбец потенциалов;
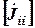– матрица-столбец узловых токов, определяемых по следующей формуле:
,
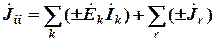В данную сумму со знаком плюс входят слагаемые, соответствующие источникам, действующим в направлении рассматриваемого узла.
С помощью полученной системы определить неизвестные потенциалы узлов.
4. Определить токи во всех ветвях и напряжение на источнике тока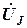 
на основании соотношений, составленных по обобщенному закону Ома.
Метод наложения
Решение задач данным методом основано на применении принципа суперпозиции (наложения), согласно которому ток в произвольной i-й ветви равен алгебраической сумме токов, создаваемых каждым источником в отдельности.
При расчете цепей методом наложения из исходной цепи получают k вспомогательных схем (подсхем), где k – число источников. В каждой из этих вспомогательных схем оставляют только один источник. Удаление источников осуществляется в соответствии со следующим правилом: источники ЭДС заменяются короткозамкнутыми участками, ветви с источниками тока размыкаются. В каждой из полученных подсхем рассчитываются составляющие соответствующих токов, создаваемые данным источником. Токи исходной цепи определяются как алгебраическая сумма соответствующих токов вспомогательных схем:
.
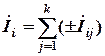