Оценка показателей качества замкнутой системы, определение нулей и полюсов передаточной функции

Студент: Мавропуло И.Н.

Группа: Н172

Преподаватель: Коробова И.Л.

Оценка:

Подпись:

Санкт-Петербург

2009г.

Техническое задание:

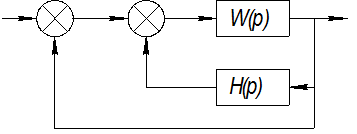
1. Определить передаточную функцию разомкнутой системы рис.1, представить её в канонической .форме. Построить её логарифмические частотные характеристики.

2. Оценить показатели качества замкнутой системы, определив нули и полюса передаточной функции.

3. Построить графики переходной функции и импульсной переходной функции, определить показатели качества переходного процесса (для оценки времени регулирования принять Δ=3%).

4. Найти аналитическое выражение переходной функции. Выделить составляющую найденной функции, соответствующую доминирующим полюсам, сравнить графики функции и указанной её составляющей.

5. Используя критерий Найквиста, дать заключение об устойчивости замкнутой системы, определить запасы устойчивости.

, .

, , , , ,

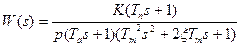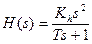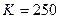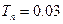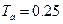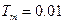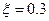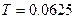
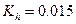
6. Построить логарифмическую амплитудно-частотную характеристику замкнутой системы, определить полосу пропускания системы, резонансную частоту, показатель колебательности.

7. Найти уравнения состояния и выхода в форме Фробениуса замкнутой системы (2 варианта). Проверить свойства управляемости и наблюдаемости этих вариантов.

1. Определение передаточной функции разомкнутой системы рис.1, представление её в канонической форме. Построение её логарифмической частотной характеристики.

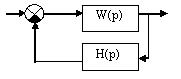
Передаточная функция разомкнутой системы: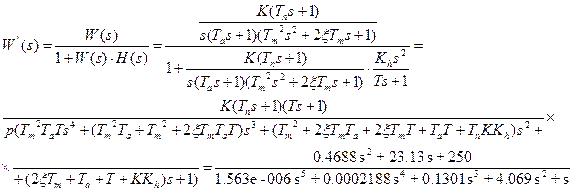

Приведем к каноническрму виду, используя >>Wz=zpk(W)

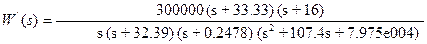
Находим ЛАЧХ и ФЧХ системы, используя пакет MATLAB:

>> num=[ 0.4688 23.1 250];

>> den=[ 1.563e-006 0.0002188 0.1301 4.069 1 0];

>> w=logspace(-1,3);

>> [gam,fi]=bode(num,den,w);

>> semilogx(w,20*log10(gam));

>> grid

>> title('L(w)')

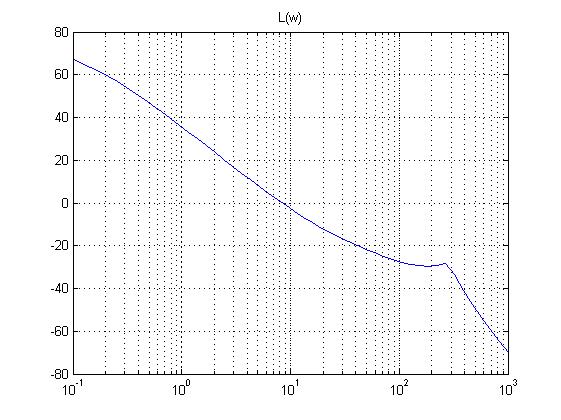
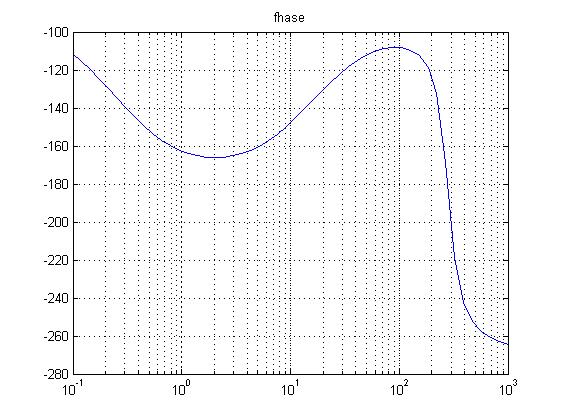
Оценка показателей качества замкнутой системы, определение нулей и полюсов передаточной функции.

Передаточная функция имеет вид:

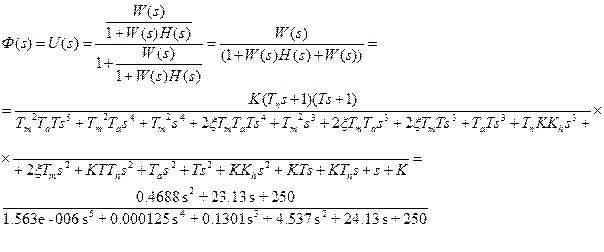
Нулями передаточной функции называются корни полинома числителя, а полюсами называются корни полинома знаменателя. Вычислим нули и полюса с помощью пакета Matlab.

>> zero(ui)

ans =

-3.333333333333334e+001

-1.600000000000000e+001

>>pole(ui)

ans =

-2.224758999602469e+001 +2.846065103522168e+002i

-2.224758999602469e+001 -2.846065103522168e+002i

-3.150315083377950e+001

-2.000834587085519e+000 +7.636564740604480e+000i

-2.000834587085519e+000 -7.636564740604480e+000i

Система устойчива, т.к. все полюса находятся в левой полуплоскости.

Показатели качества:

1. Степень устойчивости

Она характеризует быстродействие системы и равна абсолютному значению вещественной части ближайшего полюса, т.е. .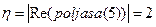

1. Время регулирования

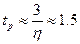с.

1. Степень колебательности

.

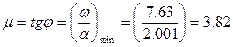Колебательность связана с корневым показателем запаса устойчивости с так называемым затуханием. Комплексно сопряженные корни дают в выражении для переходного процесса вида

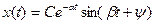
Найдем затухание амплитуды синусоидального колебания за один период. При некотором времени 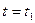эта амплитуда равна

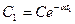
Через один период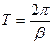

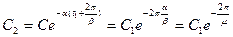
Затуханием за период называют величину

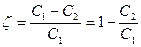
Подставляя значение амплитуды 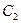, получаем

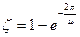
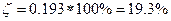
3. Построение графиков переходной функции и импульсной переходной функции, определение показателей качества переходного процесса (для оценки времени регулирования принять ∆=3%):

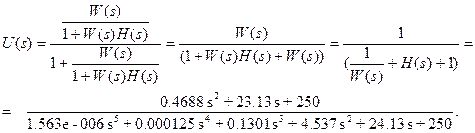
Построим графики переходных функций во временных осях, используя пакет Matlab и команды step(sys) и impulse(sys).

>>t=0:0.02:7

>>s=tf('s');

>>W=K*(Tn*s+1)/(s*(Ta*s+1)*(Tm^2*s^2+2*E*Tm*s+1))

>>H=Kh*s^2/(T*s+1)

>>U=W/(1+W*H)

>>UI=1/((1/W)+H+1)

>>step(UI,t)

>>impulse(UI,t)